对称函数的偏导数

樊自安,陈昌银

(1.孝感学院数学与统计学院,湖北孝感432000;2.孝感市孝南区毛陈中学,湖北孝感432000)

对称函数的偏导数

樊自安1,陈昌银2

(1.孝感学院数学与统计学院,湖北孝感432000;2.孝感市孝南区毛陈中学,湖北孝感432000)

对于一类特殊的函数——对称函数,给出了它的定义、性质,这些性质给偏导数的计算和证明带来很大方便。

对称函数;多元函数;偏导数

在高等数学、数学分析以及偏微分方程等课程中,有许多求偏导数的问题。有一类函数,如 u它对各个变量的偏导数存在一定的规律,如果掌握这种规律,我们只需求出其中一个变量的偏导数,另一个变量的偏导数可很快写出,而不必逐个求导。

首先看几个定义:

定义1对于二元函数z=f(x,y),用(y,x)来代替(x,y)得到的函数z=f(y,x)叫做 z=f(x,y)的转置函数,记作 z=[f(x,y)]T。

定义2对于二元函数z=f(x,y),若 f(x,y)=[f(x,y)]T,则称 z=f(x,y)为对称函数。

定义3对于多元函数 u= f(x1,x2,…,xn),用(xi,x1)来代替(x1,xi),其他自变量不变,得到的函数 u=f(x1,x2,…,xi-1,xi+1,…,xn)叫做 u=f(x1,x2,…,xn)相对于 xi的转置函数,记作 u=[f(x1,x2,…,xn)]Txi,i=1,2,…,n。

定义4对于多元函数 u= f(x1,x2,…,xn),任意互换两个自变量的位置得到的函数总与原函数相同,则称多元函数 u=f(x1,x2,…,xn)为对称函数。

下面讨论对称函数的偏导数。

1 一阶偏导数的情形

定理1若二元函数 z=f(x,y)为对称函数,它关于 x,y的两个偏导数都存在,则

证明

定理2若多元函数u=f(x1,x2,…,xn)为对称函数,它关于每个变量的偏导数都存在,则

证明

2 高阶偏导数的情形

对于二元函数和多元函数的高阶偏导数,也有类似的定理。

定理3若二元函数 z=f(x,y)为对称函数,它关于 x,y的两个二阶偏导数都存在,则

证明

定理4若多元函数u=f(x1,x2,…,xn)为对称函数,它关于每个变量的 n偏导数都存在,则

证明用数学归纳法证明。

k=2,只要把定理2证明过程中的f改为fx就可得到,假设对 k成立,则

3 复合偏导数的情形

对于复合多元函数的偏导数,有如下定理:

定理5若多元函数z=f(u1,u2,…,un)在点(u1,u2,…,un)有连续偏导数,每个函数 ui=ui(x1,x2,…,xn)为对称函数,它关于每个变量的二阶偏导数都存在,则

证明

4 几个例子

例 1设 z=exysin(x+y),求

解z=f(x,y)为对称函数。

例2验证lap lace方程的基本解

满足方程-△u=0。其中wn是n维单位球面面积,为lap lace算子。

证明多元函数为对称函数,由定理4可得:

代入即得:

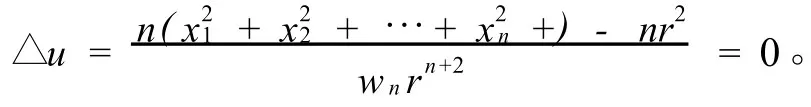
例3设z=f(x+y,xy),f具有二阶连续偏导数,求

解设z=f(u,v),u=x+y,v=xy,u,v是对称函数。由定理5得:

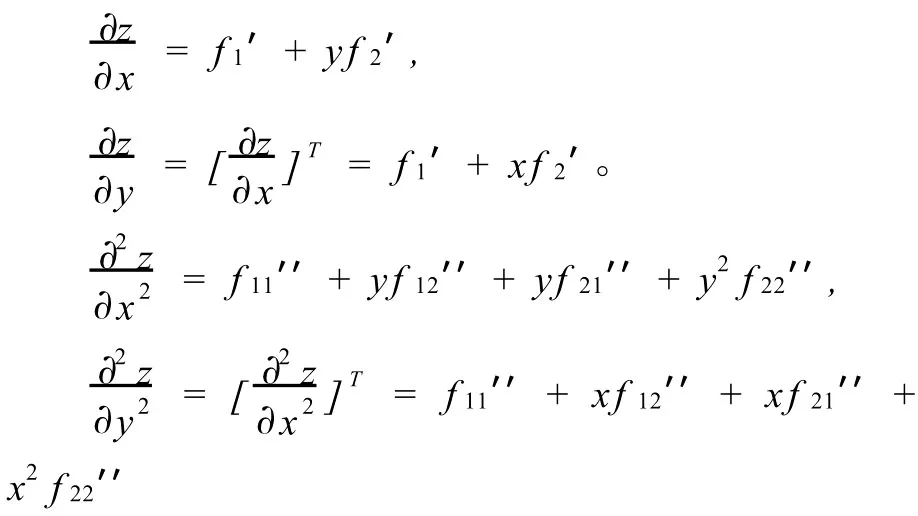
[1] 同济大学应用数学系.高等数学[M].5版.北京:高等教育出版社,2002.

[2] 华东师范大学数学系.数学分析[M].3版.北京:高等教育出版社,2001.

The Partial Derivative of Symmetric Function

Fan Zi’an1,Chen Changyin2
(1.School of M athem atics and Statistics,Xiaogan University,Xiaogan,Hubei 432000,China;2.M aochen M idd le School of Xiaonan D istrict,Xiaogan,H ubei 432000,China)

In this paper,we give definition and characteristics of partial derivative of symmetric function.These characteristics can bring conveniency to the calculation and p roof of partial derivative.

symmetric function;function of several variables;partial derivative

O172.1

A

1671-2544(2010)03-0031-03

2010-03-03

樊自安(1972— ),男,湖北孝感人,孝感学院数学与统计学院讲师,硕士。

(责任编辑:周 游)