自适应粒子群算法在非线性回归中的应用

陈高波,杨小红

(1.武汉工业学院数理科学系,湖北武汉 430023;2.武汉市慈惠中学,湖北武汉 430040)

自适应粒子群算法在非线性回归中的应用

陈高波1,杨小红2

(1.武汉工业学院数理科学系,湖北武汉 430023;2.武汉市慈惠中学,湖北武汉 430040)

采用自适应算法调整粒子群的权重,优化非线性回归模型的参数,并将其应用于酶促反应的参数求解。与线性化、非线性最小二乘以及标准粒子群的结果比较表明,用自适应粒子群求解的非线性回归方程有更高的精度。

自适应;粒子群;非线性回归

线性回归模型因其结构简单在各类建模中得到广泛应用。在社会现实经济生活中,很多现象之间的关系并不是线性关系,对这种类型现象的分析预测一般要应用非线性回归预测.通过变量代换,可以将很多的非线性回归转化为线性回归.因而,可以用线性回归方法解决非线性回归预测问题.但并非所有的非线性模型都可以线性化,即使可以转化为线性模型,也可能造成模型随机误差项性质的改变.在这种情况下,直接采用非线性最小二乘估计比较有利.但非线性最小二乘参数估计采用迭代法求解,必须先给出参数的初始值,并且求解结果比较依赖于参数初始值[1].

粒子群优化算法 (Particle Swarm Optimization,简称 PSO)源于对鸟群捕食行为的研究,是近几年进化算法研究中的一个热点,已成功应用在函数优化、神经网络训练等领域.但粒子群算法也存在易陷入局部最优的缺点.本文采用自适应算法调整粒子群的权重,优化非线性回归模型的参数,并将其应用于酶促反应的参数求解.

1 自适应粒子群算法

标准粒子群优化算法初始为一组随机粒子 (随机解),然后通过迭代寻找最优解.粒子追随两个当前最优值来更新自己,一个是粒子迄今为止寻找到的最优值,叫做个体极值 pbest;另外一个是整个粒子群迄今为止寻找到的最优值,叫做全局极值 gbest,在标准的粒子群算法中,粒子的速度和位置更新方程为：

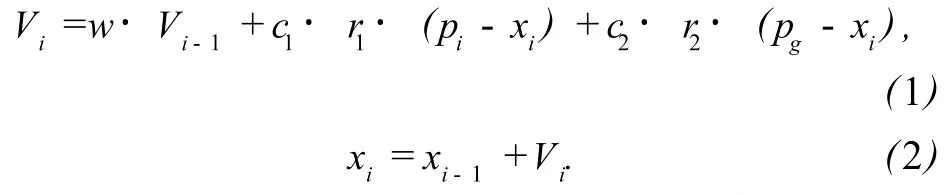
其中 Vi和 xi分别是粒子在第 i次迭代中的速度和位置,r1与 r2为 0到 1之间的随机数;c1与 c2为加速常数;w为惯性权重.

标准 PSO算法收敛速度较慢,并且易陷入局部最优.研究[2]发现较大的惯性权重 w值有利于跳出局部最优,进行全局搜索;较小的 w值有利于局部寻优,加速算法收敛.因此,为克服 PSO算法固定参数的不足,应根据群体自适应地调整惯性权重.设粒子群的大小为 n,第 i次迭代中粒子 Pi的适应值为fi,最优粒子的适应值为 fm,粒子群的平均适应值为将适应值优于 favg的适应值求平均得到 f′avg,定义对粒子的惯性权重 w调整如下[2].

1.1 当 fi优于时,这些粒子较为优秀,已接近全局最优,应赋予较小的 w,以加速向全局最优收敛.此时根据粒子适应值按式 (3)调整粒子 Pi的惯性权重,其中 wmin为 w的最小值.

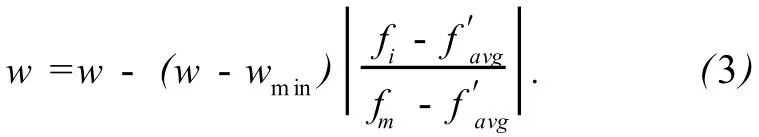
1.2 当 fi优于 favg但次于 f′avg时,这些粒子是群体中一般的粒子,具有良好的全局寻优能力和局部寻优能力,故不需改变其惯性权重 w.

1.3 当 fi次于时,这些粒子为群体中较差的粒子,按式 (4)调整粒子 Pi的惯性权重.若粒子分布较为分散,则Δ较大由式 (4)可降低粒子的惯性权重w,加强局部寻优,以使群体趋于收敛;若粒子分布较为聚集 (如算法陷入局部最优),则Δ较小,由式 (4)增加粒子的惯性权重w,使粒子具有较强的探查能力,从而有效地跳出局部最优.

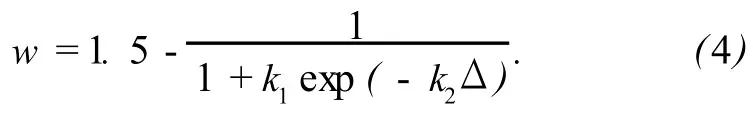
2 基于自适应粒子群的非线性回归参数估计

选取文献 [3]的酶促反应的例子.当底物浓度较小时,酶促反应速度大致与底物浓度成正比;当底物浓度很大、渐近饱和时,反应速度趋于固定值.实验表明,酶促反应的反应速度与底物浓度之间的关系可用米氏 (Michaelis)方程表示.米氏方程中参数β1为最大反应速度,可用于计算酶的催化常数,而催化常数越大,表示酶的催化效率越高;参数β2为米氏常数,即酶促反应速度达到最大反应速度一半时所对应的底物浓度,是酶的特征常数之一,在临床酶学分析中有重要意义.需要根据如表1的实验数据求出酶促反应的参数β1,β2.该问题是一典型的非线性回归问题.

表1 酶促反应速度与底物浓度数据

将 y=β1x/(β2+x)线性化可得利用线性回归可求得β1=195.8,β2=0.04841.以线性回归的参数值为初值,直接采用非线性最小二乘估计可得β1=212.68,β2=0.0641.

采用自适应粒子群算法求解参数β1,β2,目标函数为观测值与预测值的相对误差,即

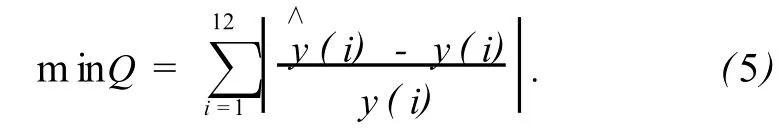
自适应粒子群 (APSO)参数取值为：粒子群规模 40,粒子维数 2(对应β1,β2两个参数),最大迭代次数 100,惯性权重范围为 (0.5,0.95),加速常数 c1=c2=2,权重调整参数 k1=1.5,k2=2.APSO求解参数β1,β2的结果见表2.为便于对比,表2同时给出了利用线性化 (LR)、非线性最小二乘 (NLR)和标准粒子群(PSO)求得的参数值.

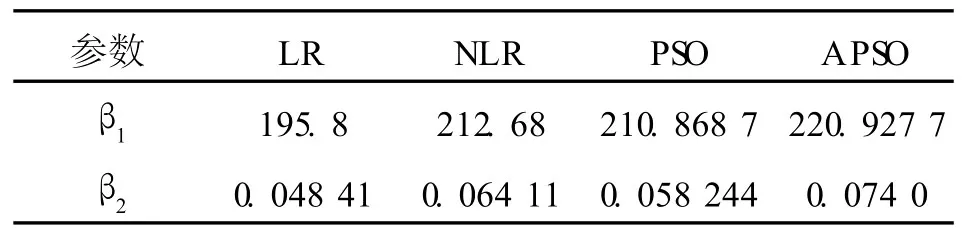
表2 LR、NLR、PSO和 APSO求解参数

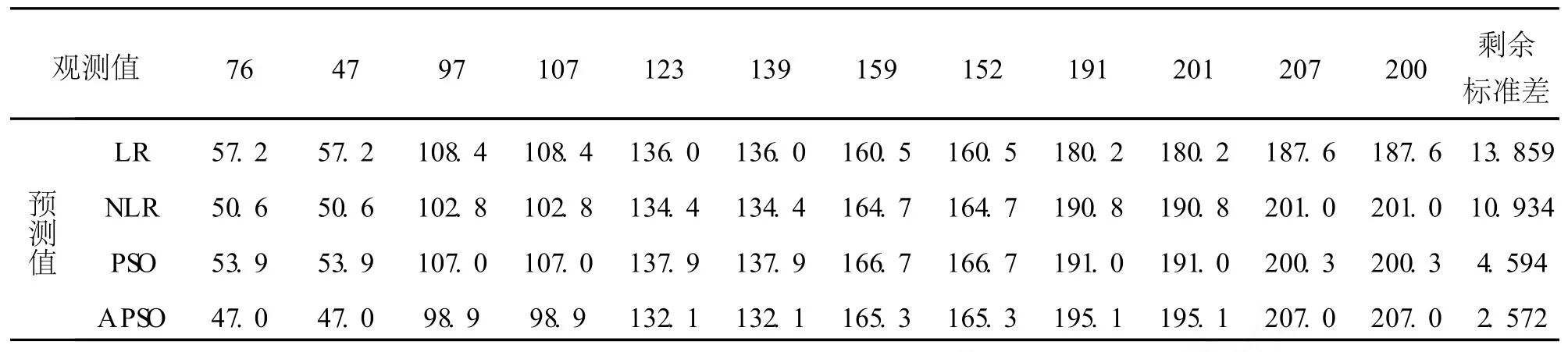
表3 LR、NLR、PSO和 APSO预测结果比较

虽然酶促反应模型可以线性化,但线性化后的模型剩余标准差(13.859)比较大,这是因为线性化导致模型随机误差项不再符合线性回归的要求;非线性最小二乘估计采用线性回归的结果作为参数初始值,模型剩余标准差 (10.934)有所降低;标准粒子群算法的参数寻优结果要好得多,剩余标准差降为 4.594;自适应权重调整的粒子群的参数估计结果最好,模型剩余标准差仅为 2.572.因此用自适应粒子群(APSO)算法求解酶促反应的非线性回归方程是可行的,并且回归方程的精度更高.

3 结束语

采用粒子群算法优化非线性回归问题的参数,惯性权重自适应调整既有利于全局搜索又利于局部寻优.对酶促反应的参数估计结果表明,自适应粒子群算法用于求解非线性回归方程的参数有其独特的优势.

[1] Douglas M.Bates.非线性回归分析及其应用[M].北京：中国统计出版社,1997.

[2] 韩江洪,李正荣,魏振春.一种自适应粒子群优化算法及其仿真研究[J].系统仿真学报,2006,18(10)：2969-2971.

[3] 姜启源,谢金星,叶俊.数学模型 (第三版)[M].北京：高等教育出版社,2003.

[4] 刘蓉生.试验数据及图像计算机处理 [M].北京：清华大学出版社,2005.

Application in nonlinear regression of adaptive particle swarm optim ization

CHEN Gao-bo1,YANG Xiao-hong2
(1.Department of Mathematics and Physics,Wuhan Polytechnic University,Wuhan 430023,China;2.Wuhan Cihui School,Wuhan 430040,China)

An adaptive weights adjustment algorithm for particle swar m optimization is adopted to opt imize the parameters of nonlinear regression model in this paper.The adaptive particle s warm optimization is used to solve the parameters of enzyme catalytic reaction.Compared with linearation,nonlinear least square and standard particle s warm opt imization,the results show that nonlinear regression equation based on adapative particle s warm optimization has higher precision.

adaptive;particle s warm optimization;nonlinear regression

O 22

A

1009-4881(2010)01-0100-03

10.3969/j.issn.1009-4881.2010.01.027

2009-08-29.

陈高波 (1972-),男,讲师,E-mail：chengaob@126.com.

湖北省教育厅科研项目(Q20091809);武汉工业学院基金资助项目(08Y30).