四维复欧氏空间单位球面中的一类浸入环面

邓俐伶,侯中华

（1.大连民族学院理学院,辽宁大连 116605; 2.大连理工大学数学科学学院,辽宁大连 116023）

四维复欧氏空间单位球面中的一类浸入环面

邓俐伶1,侯中华2

（1.大连民族学院理学院,辽宁大连 116605; 2.大连理工大学数学科学学院,辽宁大连 116023）

所研究的对象是源于小波分析滤波器构造理论中提出的几何模型,即一类四维复欧氏空间单位球面中的浸入环面问题,特点是其参数表示中的4个坐标分量函数均为实系数二元多项式。首先根据环面的参数表示得到了多项式系数所满足的约束条件方程组;在此基础上考虑了多项式次数n=1时的情形,得出了此时该环面不可能为全测地浸入的结论;从而以新的研究方法验证了欧氏空间中不存在全测地环面子流形这一事实。

复欧氏空间;全测地;浸入;运动方程

关于小波分析滤波器构造理论,文献[1]清晰地描述了一类二维正交滤波器,包括线性相位的情形,并给出了一些例子。文中还介绍了一种较有名的构造方法MRA,它是由一簇满足某些条件和性质的子空间构成的序列;在某种情形下,尺度函数所满足的关系式等价于（把满足这个条件的多项式组称为多相系）,即环面模型。纪永强[2]认为,由于曲面为全测地子流形的充要条件是它的任意一条测地线必为其大空间内的测地线,而欧氏空间中的测地线均为直线,故欧氏空间中不可能存在球面或环面子流形。本文在前人研究基础上结合环面模型自身特点,从新的研究角度重新验证了这一结论。首先借助于多项式的表示与坐标变换,运用微分法和三角函数系的正交性得出多项式系数满足的约束条件方程组;在此基础上根据自然标架的运动方程,采用反证法证明了当多项式次数n=1时该环面不可能为全测地浸入的结论,同时也为进一步探讨高次数多项式及其他复杂情形下环面的存在性建立了研究基础。

1 浸入环面的参数表示及性质

1.1 浸入环面的参数表示

1.2 坐标函数fk（eiξ,eiη）（k=1,2,3,4）的性质

2 全测地浸入环面不存在的证明

2.1 多项式系数满足的约束条件方程组

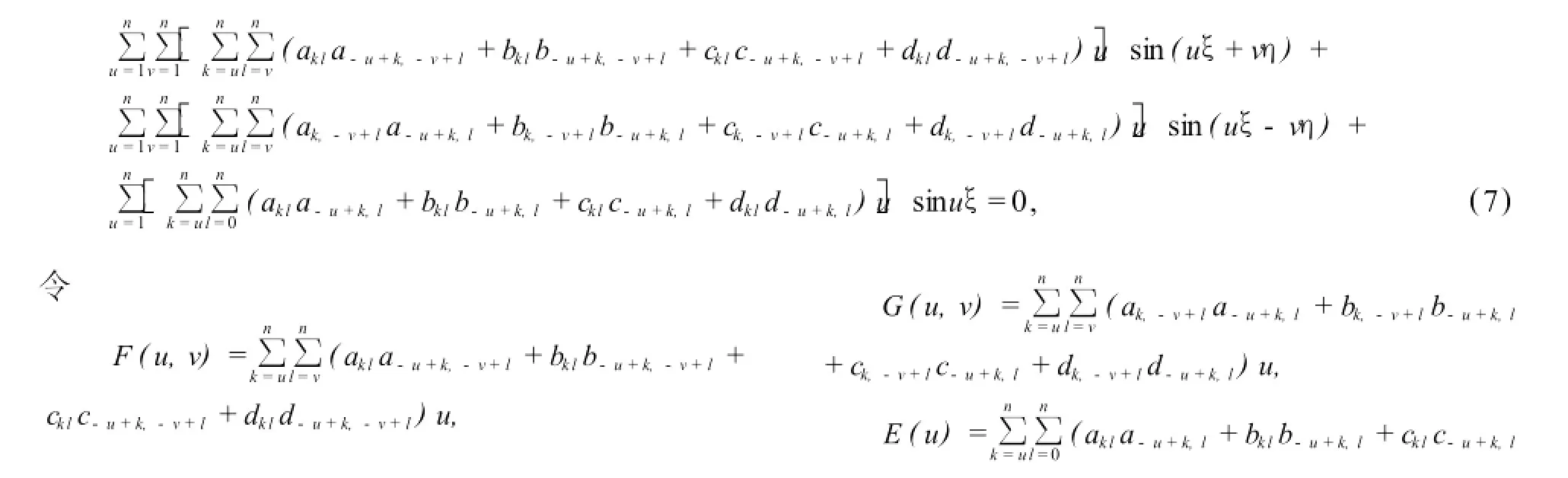
式（8）是多项式fk的系数满足的第一个约束条件方程组。观察可知它含2n2个方程,而变量却有4（n+1）2个,因此有必要进一步增加约束条件。

2.2 n=1时全测地浸入环面S不存在的证明

考虑最简单的情形,即当n=1时,式（8）化为

对式（10）中（C）式,令ξ=0,η=0,由两边实部相等可得

3 结 语

本文研究的环面模型是一类四维复欧氏空间单位球面中的浸入,其特点是每个坐标函数均为实系数二元多项式。文中使用微分法、活动标架法及三角函数系的正交性等数学工具得出多项式系数所满足的约束条件方程组,并在此基础上证明了在最简单的情形即多项式次数n=1时,该类全测地浸入环面不存在的结论。

[1]SILongpeng.Construction of t wo-dimensional compactly supported orthogonal wavelets filters with linear phase [J].Acta Mathematica Sinica:English Series,2002,18 （4）:719-726.

[2]纪永强.子流形几何[M].北京:科学出版社,2004.

[3]陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社,2001.

[4]彭家贵,陈卿.微分几何[M].北京:高等教育出版社,1988.

[5]吕林根,许子道.解析几何[M].北京:高等教育出版社,2001.

Torus Immersed in the Un it Sphere in the Four-dimensional Complex Euclidean Space DENG L i-ling1,HOU Zhong-hua2

（1.School of Science,Dalian NationalitiesUniversity,Dalian Liaoning 116605,China; 2.School ofMathematical Sciences,Dalian University of Technology,Dalian Liaoning 116023,China）

The subject comes from geometric models proposed by the theory ofwavelet filter construction.In otherwords,it is torus immersed in the unit sphere in the four-dimensional complex Euclidean space,whose four coordinate functions in its parametric expressions are all bivariate polynomialswith real coefficients.First,the constraint equations of those coefficients are obtained based on the parametric expressions.Then the case where the degree of the polynomial n=1 is considered;it is concluded that the torus cannot be totally geodesic,providing a new proof of the fact that it is impossible to find any torus totally geodesic in Euclidean space.

complex Euclidean space;totally geodesic;immersion;equations ofmotion

O186

A

1009-315X（2010）01-0040-04

2009-07-24

邓俐伶（1982-）,女,辽宁大连人,助教,主要从事微分几何研究。

（责任编辑 邹永红）