求解非线性优化问题的一个非线性Lagrange函数

王 炜,田珍菊,姜 珊

（辽宁师范大学数学学院,辽宁大连 116029）

求解非线性优化问题的一个非线性Lagrange函数

王 炜,田珍菊,姜 珊

（辽宁师范大学数学学院,辽宁大连 116029）

提出了一个求解非凸的具有不等式约束的非线性优化问题的一个非线性Lagrange函数,并讨论了在K-T点的性质。收敛定理表明,在适当的条件下,当参数k大于某一阈值k0时,产生的点列具有局部收敛性,由此给出了与罚参数相关的解的误差估计。

非线性Lagrange函数;非线性优化;收敛性

1 非线性Lagrange函数的提出

考虑具有不等式约束的非线性规划问题:

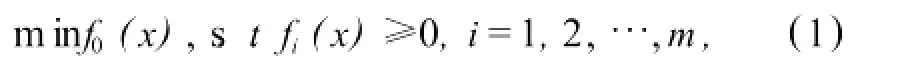
本文提出另一个解决非凸规划问题的非线性Lagrange函数

2 主要结论的证明

2.1 非线性Lagrange函数G（x,μ,k）的性质

非线性Lagrange函数（2）在K-T点（x＊,μ＊）处具有如下性质:

2.2 非线性Lagrange函数G（x,μ,k）的对偶算法的收敛性定理

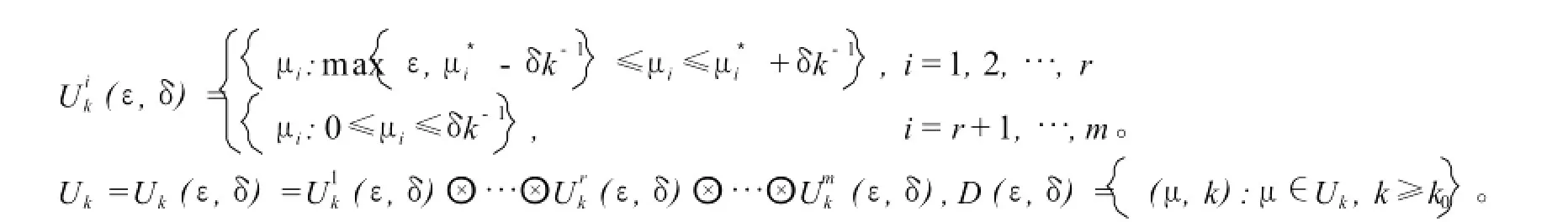
3 结 语

本文的论证说明了G（x,μ,k）具有很好的性质,在适当的条件下,基于该函数的迭代点列具有局部收敛性,并且给出了解的误差估计,为解决非线性优化问题提供了一个新的途径。关于G（x,μ, k）的对偶理论及数值结果将会在其他文章中研究。

[1]BERTSEKAS D.Constrained Opti mization and Lagrange MultiplierMethods[M].New York:Academic Press, 1982.

[2]POLYAK R A.Modified barrier function:theory and methods[J].Mathematical Progamming,1992,54（2）: 177-222.

[3]FI ACCO A V,MCCORM ICK G P.Nonlinear Programming:Sequential Unconstrained MinimizationTechniques[M].New York:W iley,1968.

[4]POLYAK R A.Log-Sigmoid multipliersmethod in constrained optimization[J].Annals of Operations Research,2001,101:427-460.

A Nonlinear Lagrangian for Nonlinear Optim ization WANGW ei,TIAN Zhen-ju,JING Shan

（School ofMathematics,LiaoningNormalUniversity,Dalian Liaoning 116029,China）

This paperproposes a nonlinearLagrangian for solving nonconvex,nonlinearoptimization problems with inequality constraints.It discusses properties of the function at the K-T point.The convergence theorem shows that the sequence of iterate points generated based on the proposed nonlinearLagrangian is locally convergentwhen the penalty k parameter is larger than a threshold k0under a set of suitable conditions on problem functions,thereby giving the error estimate for the solution,depending on the penalty parameter.

nonlinearLagrangian function;nonlinear optimization;convergence

O221.2

A

1009-315X（2010）01-0031-04

2009-07-11

辽宁省教育厅高等学校科研项目（2008376）。

王炜（1960-）,女,辽宁本溪人,教授,博士,硕士生导师,主要从事运筹学与控制论研究。

（责任编辑 邹永红）