混沌与拓扑半共轭

王立冬,杨玉娥

（1.大连民族学院理学院,辽宁大连 116605;2.辽宁师范大学数学学院,辽宁大连 116029）

混沌与拓扑半共轭

王立冬1,杨玉娥2

（1.大连民族学院理学院,辽宁大连 116605;2.辽宁师范大学数学学院,辽宁大连 116029）

（X,f）与（Y,g）为拓扑动力系统,f与g是拓扑半共轭的,对基于拓扑半共轭特殊性质扩充的混沌性进行了探讨,作为应用,给出了区间映射拓扑熵大于0与几乎周期点集中有不可数混沌集是等价的一个新的证明。

拓扑半共轭;几乎周期点;混沌

自Li-Yorke用严格的数学定义混沌之后,人们从不同角度对混沌进行深入研究,1994年Schwerizer与Smital提出了分布混沌概念,说明了区间映射的分布混沌与正拓扑熵等价,因此讨论正拓扑熵与Li-Yorke混沌关系是十分有意义的。熊金城提出熊混沌[1],并讨论了熊混沌与拓扑弱混合的关系。而周作领[2]提出了测度中心的概念,并指出测度中心的极小集是它本身,说明在极小集上讨论问题具有重要意义。本文对拓扑半共轭性质的扩充的混沌性进行了讨论,其主要结果如下:

定理1令（X,d1）,（Y,d2）为紧度量空间, （X,f）与（Y,g）为拓扑动力系统,Φ:X→Y为f与g的拓扑半共轭,如果g有极小混沌集Γ且存在y0∈Γ满足#Φ-1（y0）=1,则（X,f）是混沌的。

定理2设（X,f）为拓扑动力系统,Φ:X→∑2为f与σ的拓扑半共轭,如果存在y0∈∑2满足# Φ-1（y0）=1则f有不可数混沌集Γ⊂A（f）。

1 基本定义与引理

空间（∑,ρ）是紧的度量空间,称其为两个符号的单边符号空间。

定义σ:∑→∑为对∀x=x0x1…∈∑,σ（x0x1…）=x1x2…,则σ是连续的,称为∑上的移位映射,因此（∑,σ）为紧系统。

定义1称x是几乎周期的,如果对任意的ε＞0,存在整数N＞0,使得对任何q≥0,存在整数r,q＜r≤q+N满足d（fr（x）,x）＜ε。f的全体几乎周期点的集合记作A（f）。

定义2设（X,f）,（Y,g）都是动力系统,f,g都是连续映射,如果存在满射h:X→Y使得对任何x∈X,都有h（f（x））=g（h（x））,则称f与g拓扑半共轭。

定义3设（X,f）为紧致系统,f:X→X是连续映射,Y⊂X,{pi}是给定的正整数递增序列,如果对任意连续映射g:Y→X,存在序列{qi}⊂{pi}使得则称Y是f相对于序列{pi}而言的一个熊混沌集,称f为在Y上关于序列{pi}熊混沌的。

定义4设（X,d）是紧致度量空间,f:X→X是连续映射,如果存在集合D⊂X,使得对∀x,y∈D,x≠y有

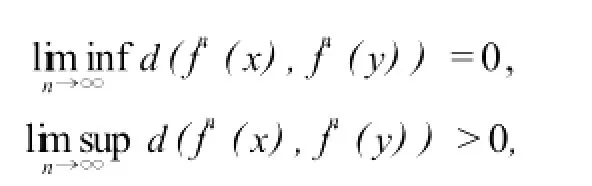
则称D是映射f的一个Li-Yorke混沌集;如果存在映射f的一个不可数的Li-Yorke混沌集,则称映射f是Li-Yorke混沌的,简称混沌的。

定义5（X,f）称为弱混合的,如果f×f:X×X→X×X是传递的。

定义6对每个ε＞0,x∈X,都存在n＞0满足fn（V（X,ε））∩V（x,ε）≠φ,则称x为X中非游荡点。所有非游荡点构成的集合记为Ω（f）。

引理1[3]设f:X→X和g:Y→Y是连续的,其中X和Y是紧度量空间,如果存在一个连续的满射h:X→Y使得g°h=h°f,则

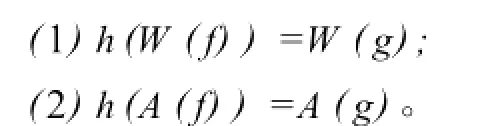
引理2[4]（∑,ρ）为两个符号的单边符号空间,σ为其上的移位映射,存在一个极小集τ⊂∑满足σ|τ是弱混合的。

引理3[5]设f:X→X是一连续映射,其中X是至少包含两个点的局部可分的紧致度量空间,则f是拓扑弱混合的当且仅当存在X的一个c-稠密Fσ型熊混沌子集。

引理4[6]设f:I→I是连续映射,则f在Ω（f）上是混沌的当且仅当ent（f）＞0。

引理5[7]设f:I→I是连续映射且ent（f）＞0,则存在闭集X⊂I,m＞0满足fm（X）=X。且fm|X至多2对1的拓扑半共轭到单边移位映射σ,而且在∑中只有可数多个点有两个原像,如果有一个原像是周期的,则其他的也是周期的。

2 定理证明

综上,f有不可数混沌集且其中每个点都是几乎周期。

3 定理应用

作为两个定理的应用,证明下面条件是等价的。

令f:I→I连续映射,1）ent（f）＞0;2）A（f）中有不可数混沌集。

证明1）⇒2）由引理5,存在闭集X⊂I,m＞0满足fm（X）=X。fm|X至多2对1的拓扑半共轭到单边移位映射σ,且在∑中只有可数多个点有两个原像。所以存在一个连续满射h:X→∑使得h°fm=σ°h,存在y0∈∑使得#Φ-1（y0）=1。由定理2可知,有fm的一不可数混沌集Γ⊂A （fm）,进而可知f有不可数混沌集Γ⊂A（f）。

2）⇒1）因为A（f）⊂Ω（f）,所以Ω（f）上存在不可数混沌集,通过引理4可证ent（f）＞0。

[1]XI ONG Jingcheng,YANG Zhongguo.Chaos caused by a topologically mixing map,Indynamical Systems and Related Topics[M].Singapore:World Scientific Press, 1992.

[2]周作领.弱几乎周期点与测度中心[J].中国科学:A辑,1992,22（6）:572-581.

[3]周作领,何伟弘.轨道结构的层次与拓扑半共轭[J].中国科学:A辑,1995,25（5）:457-464.

[4]WANGLidong,CHEN Zhizhi,LI AO Gongfu.The complexity of amini mal sub-shifton sy mbolic spaces[J].Mathematical Analysis andApplications,2006,317:136-145.

[5]杨润生.按序列分布混沌和拓扑混合[J].数学学报, 2002,45（4）:753-758.

[6]周作领.紊动与拓扑熵[J].数学学报,1988,31（1）: 83-87.

[7]L I Shihai,W-Chaos and topological entropy[J].Transactions of the American Mathematical Society,1993, 339:243-249.

Chaos and Topological Sem i-conjugacy
WANG L i-dong1,YANG Yu-e2

（1.College of Science,Dalian NationalitiesUniversity,Dalian Liaoning 116605,China; 2.Department ofMathematics,LiaoningNormalUniversity,Dalian Liaoning 116029,China）

Let（X,f）,（Y,g）be topological dynamical systems,wherefandgare topologically semi-conjugate.This paper presents chaoticity as an extension that is based on special properties of topological semi-conjugacy.As an application,it gives a new proof for the fact that the topological entropy of intervalmaps being greater than 0 is equivalent to a set of almost periodic points containing an uncountable chaotic set.

topological semi-conjugacy;almost periodic points;chaos.

O189

A

1009-315X（2010）01-0024-03

2009-09-21

国家民委自然科学基金资助项目（07DL05）;辽宁省教育厅基金资助项目（2009A141）。

王立冬（1955-）,男,吉林德惠人,教授,博士,学校优秀教学带头人,硕士生导师,主要从事拓扑动力系统研究。

（责任编辑 邹永红）