增长曲线模型误差方差的二次型可容许估计*
2010-01-08张立振刘利贞
张立振,刘利贞
(中国海洋大学数学科学学院,山东青岛266100)
增长曲线模型误差方差的二次型可容许估计*
张立振,刘利贞
(中国海洋大学数学科学学院,山东青岛266100)
对于增长曲线模型,在二次损失函数下,研究了当C为列满秩,而A为行秩亏矩阵时误差方差的二次型估计的容许性,用矩阵形式给出了二次型估计可容许的充要条件。
增长曲线模型;误差方差;二次型估计;容许性
1 问题与结果
关于线性模型误差方差的二次型容许估计问题已经由吴启光、成平、李国英[1-2]、徐兴忠[3]得出完整的结论。本文研究具有多方面应用的增长曲线模型中误差方差σ2的二次型容许估计问题。增长曲线模型是由Potthoff和Roy[4]提出的多元方差分析模型。后被许多学者如:Rao、Khatri、Von Rosen等加以研究。增长曲线模型在经济、生物、医药等领域都有重要地应用。近来,国内也对这一模型进行了广泛的研究,如覃红、陈峥、张东华、王欣等研究了回归系数的容许估计问题。尤进红、王志忠、刘锋、张尚立和桂文豪等研究了协方差估计在不同条件下的容许性问题。增长曲线模型如下:

对于此模型,张立振、徐兴忠[5]在二次损失函数(d-σ2)2/σ4下,对于行满秩和A=1n,C′=1p2种特殊情况,研究了σ2的二次型估计tr(Y′MY)在={tr(Y′MY):Mn×n≥0}(下文中皆表示此估计类)中的容许性。张立振[6]在假定H:G=In,rank(A)=r 结论1 对于模型(1),在H条件下,tr(Y′MY)是σ2在中容许估计的必要条件是Y′MY必须具有形式:Y′[a(I-P)+PNP]Y。并且a≥0,Nn×n≥0还要满足其中:P=A(A′A)-A′,是PNP的非零特征根,b=max(a,λ1),rank(A)=r 结论2 对于模型(1),在假定H下 (Ⅰ)tr{Y′(I-P)/[(n-r)p+2]Y}是σ2在中的容许估计。 (Ⅱ)设M≥0,MA=0但M≠(I-P)/[(n-r)p+2],则tr(Y′MY)非容许。(P的意义同结论1) 本文在假设H1:G=In,rank(A)=r 定理 设a>0,rank(PNP)=s≥1,对于模型(1),G=In,在假设H1下,tr{Y′[a(I-P)+PNP]Y}是σ2在中容许估计的充要条件为:不存在d>0使 对α∈(R*)ps皆成立。 注1 当C=(1),p=1时,增长曲线模型(1)变为线性模型。在此种情况下 (Ⅰ)由本文定理可得出文献[3]中引理1的结论。 (Ⅱ)由本文推论1可得出文献[2]中引理2.5的结论。 (Ⅲ)由本文推论2可得出文献[2]中定理2.1的结论。 文献[6]中(3)式得出tr{Y′[a(I-P)+PNP]Y}在损失函数(d-σ2)2/σ4下的风险函数为: 其中:θ=vec(B)/σ∈Rm·q是未知参数向量。 引理1 设B,A分别为p×q,n×m矩阵,则B“A行满秩ΖB,A皆行满秩。 证明 (证明略) 引理2 当a=0,N≥0且N≠0时,tr{Y′[a(I-P)+PNP]Y}非容许。 R[θ,a1(I-P)+PN1P]≤R(θ,PNP)成立,从而tr{Y′[a(I-P)+PNP]Y}非容许。(证毕) 构造n阶正交矩阵Γ=(Γ1Γ2),其中Γ1是n×r阶矩阵块,且L(Γ1)=L(A)。(L(A)表示A的列向量构成的线性空间,下文的Γ1皆与此处含义相同)则Γ′2A=0。于是 对一切θ∈Rm·q皆成立,并且对某个θ0∈Rm·q严格不等号成立。引进记号: 由于tr{Y′[a1(I-P)+PN?1P]Y}一致优于tr{Y′[a(IP)+PNP]Y},所以Ip“diag(λ1,…,λs,0,…,0)≥Ip“D,故diag(λ1,…,λs,0,…,0)≥D,而D≥0所以D=,其中D1为s阶方阵。(Ⅰ)当D为对角形矩阵时,显然有T′diag(d1,…,ds,0,…,0)T=Γ′1N?1Γ1=Γ′1N1Γ,从而有(5)式成立。(Ⅱ)当D不为对角形矩阵时,其证明过程与文献[7]中引理4.20的证明过程完全类似。故从略。引入记号: 证明 (充分性)若tr{Y′[a(I-P)+PNP]Y}不是σ2在中容许估计,由引理3知,一定存在a1>0,N1≥0使 对一切α∈(R*)p·s皆成立,且对某个α0∈(R*)p·s严格不等号成立。其中τ为由PN1P的特征根构成且与λ有相同维数的列向量。从而有 对α∈(R*)p·s皆成立。从而(10)式≤ 其中 对于k与l∈(R*)p·s任意的取值,都有g(α)→0(当‖α‖→0时)。故当‖α‖→0时,(2)式左边的极限≤0。因此对于k与l∈(R*)p·s任意的取值,不可能存在常数d>0使(2)式对α∈(R*)p·s皆成立。由本文定理知推论1成立。 (证毕) 若-[(n-r)p+2]a2+a+2[(n-r)p+2]aλs-存在k及lij=λj(i=1,…,p;j=1,…,s),使Δ极小<0,从而存在常数d>0使(2)式对α∈(R*)p·s皆成立。(证毕) [1] 吴启光,成平,李国英.线性模型中误差方差的二次型估计的可容许性问题[J].中国科学A辑,1981,24(7):815-825. [2] 吴启光,成平,李国英.再论线性模型中误差方差的二次型估计的可容许性问题[J].系统科学与数学,1981,6(1):112-127. [3] 徐兴忠.线性模型中误差方差的二次型估计是—可容许估计的充要条件[J].应用数学学报,1992,15(3):410-427. [4] Potthoff R F,Roy S N.A generalized multivariate analysis of variance model useful especially for growth curre problems[J].Biometrika,1964,51(3-4):313-326. [5] 张立振,徐兴忠.两类增长曲线模型误差方差估计[J].青岛海洋大学学报,1997,27(1):121-125. [6] 张立振,赵建昕.增长曲线模型误差方差的二次型估计可容许的必要条件[J].中国海洋大学学报:自然科学版,2004,34(2):325-328. [7] 陈希儒,陈桂景,吴启光,等.线性模型参数的估计理论[M].北京:科学出版社,1985. The Admissible Quadratic Estimate of Error Variance on Growth Curve Model ZHANG Li-Zhen,LIU Li-Zhen The growth curve model.When matrixChas full column rank andAis row rank defecient,under the quadratic loss function,a necessary and sufficient condition that quadratic estimate of error variance is admissible is given with matrix form. growth curve model;error variance;quadratic estimate;admissibility O212 A 1672-5174(2010)09-154-05 国家自然科学基金项目(41076006);国家高技术研究发展计划项目(2007AA09Z118)资助 2009-05-11; 2010-05-26 张立振(1962-),博士,副教授。E-mail:goldfield@ouc.edu.cn AMS Subject Classfication: 62H12 责任编辑 朱宝象


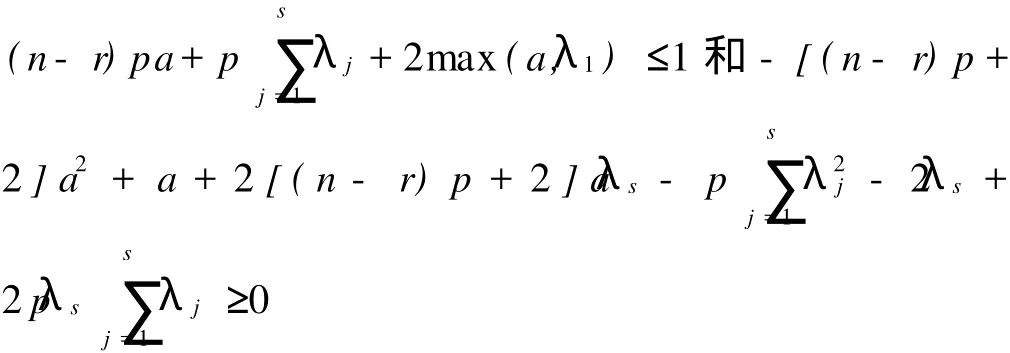

2 定理的证明
2.1 引理及其证明






2.2 定理的证明
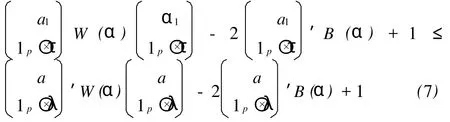



3 推论的证明
3.1 推论1的证明


3.2 推论2的证明

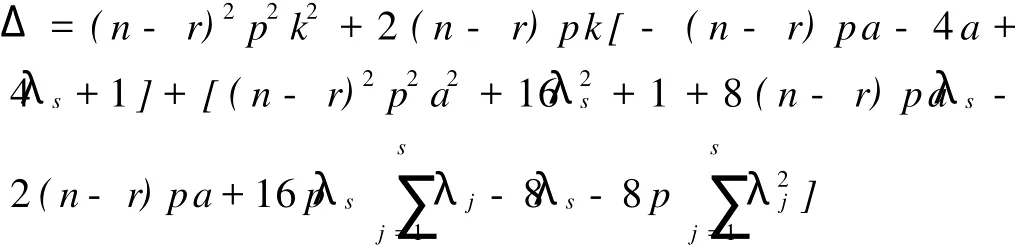

(School of Mathematical Sciences,Ocean University of China,Qingdao 266100,China)
