带机械臂的月面巡视探测器的路径规划方法研究

李群智 申振荣 张 伍 贾 阳

(北京空间飞行器总体设计部,北京 100094)

1 引言

月球是人类向外层空间发展的理想中转基地和前哨站。目前,包括中国在内的世界多个国家的研究机构均开展了对月探测的研发工作[1-2]。其中,路径规划的研究[3],作为月面巡视探测器(简称巡视器)进行巡视探测的前提和基础,直接影响巡视探测的效率,即影响地面遥操作和巡视器自主运行的工作效率,同时,会影响巡视器的生存安全。因此,开展巡视器路径规划的研究,具有重要的意义和工程实用价值。

经研究发现,巡视器在月面进行巡视探测,其运动主要包括移动和机械臂携带有效载荷运动两个方面的内容[4]。针对这两个方面,本文开展了带机械臂的月面巡视探测器的路径规划方法研究,主要内容包括:巡视器移动的路径规划(简称巡视器的路径规划)、巡视器机械臂的路径规划(简称机械臂的路径规划)、巡视器携带机械臂就位探测时巡视器与机械臂的路径规划(简称器臂动态联合的路径规划)。

2 巡视器的路径规划方法

巡视器的路径规划方法(Lunar Rover Path Planning M ethod, LRPPM)是指在一个可视区域内,巡视器以某一个或几个因素作为优化条件,发现较优行进路线的过程。与地面的自主移动机器人不同,巡视器在完成路径规划的过程中,只能靠自身的环境建模和航位推算,而不能借助外部的导航和标定系统,路径规划过程具有动态性和不完整性。此外,路径规划还需要考虑能量的限制、巡视器运行的安全性和平稳性、车体的最小转弯半径、适宜弧线、越障通过能力等特殊要求。本文巡视器的路径规划方法涉及到环境表达、路径评估和路径搜索。

针对月面环境以非结构化为显著特征,巡视器的路径规划基于三维数字高程图(DEM),采用改进的A*算法完成路径的搜索与择优。

2.1 环境表达

月面巡视探测器所在环境是实际的物理环境,而进行路径规划需要将物理环境抽象成为能被计算机理解和表达的环境模型,称为环境建模,即地图创建(M ap-building)[5]。地图创建首先要确定环境地图的描述方法,即数字地图的表示方法,必须便于计算机存储和处理。目前各国研究者已经提出了多种表示方法,常用的环境建模方法有栅格法、几何法、C 空间(C-space)法和拓扑图等。每种数字地图的表示方法都有自己的优点和缺点,根据月面巡视探测器环境感知的特点,一般采用栅格法。

基于栅格的环境表示方法最早由Elfes 和M orave 提出[6]。所谓栅格法就是将地形环境用栅格进行覆盖,每个栅格的属性值代表所覆盖地形的属性,如高度属性或区域属性(自由空间或障碍物等)。最简单的栅格法是将地图分成大小相同的栅格,这样地图就可以用数组或矩阵表示,数组的索引号与栅格在地图中的位置对应,而元素值则与栅格属性对应,形成数字高程图(DEM)。

利用栅格法进行环境建模时,一般规定只能向其水平和竖直方向的相邻栅格中心移动(称为4-邻域移动)或向其周围相邻的八个栅格中心移动(称为8-邻域移动)。栅格法的优点包括:栅格法容易创建和维护,便于计算机存储、处理和使用;在路径搜索时,栅格对应图的节点,节点间连通性已经暗含在栅格的相邻性当中,便于算法搜索。栅格法的缺点包括:空间效率不高;栅格的大小影响搜索路径的完备性;4-邻域或8-邻域移动准则限制搜索路径的最优性。但是,栅格法的这些缺点可以通过改进搜索算法和进行规划路径的后续处理来克服。

因此,本文采用栅格的描述方法来对月面环境进行描述,充分考虑巡视器的可通过性,给不同地形对应的栅格赋予不同的值,并在此基础上进行路径评估与路径搜索。

2.2 改进的A*算法

路径规划的评估与搜索是路径规划的核心内容。国外应用过的路径规划搜索算法包括启发式搜索(A*)算法研究、几何搜索算法研究和统计搜索算法研究等。巡视器路径规划方法根据不同的原则可以有不同的分类方法,按是否使用智能算法大致可以分为传统方法和智能方法[7]。根据工作环境,路径规划模型可分为全局路径规划和局部路径规划[8]。在巡视探测器中,使用得比较多的是人工势场法、A*算法和动态启发式搜索(D*)算法[3]、广度优先(Bug)算法、深度优先(ISE)算法等。本文路径规划的方法采用了具有启发、智能和全局特性的改进的A*算法。

A*算法使用了启发式方法,这种方法通过充分利用图给出的信息来动态地做出决定,使搜索次数大大降低。它通过一个评估函数(Heuristic Function)f(n)来估计图中的当前点到终点的距离(带权值),并由此决定它的搜索方向,当这条路径失败时,它会尝试其它路径。A*算法成功与否的关键在于评估函数的正确选择。

A*算法的评估函数为

式中,n 为搜索路径, f(n)为预测的全程移动消耗,g(n)为从起点到当前点的实际移动消耗,h(n)为当前点到终点的移动消耗估计值。

本文选取只对目标点感兴趣的Manhattan 估算函数作为启发因子,以达到最佳运算效率。M anhattan 距离为

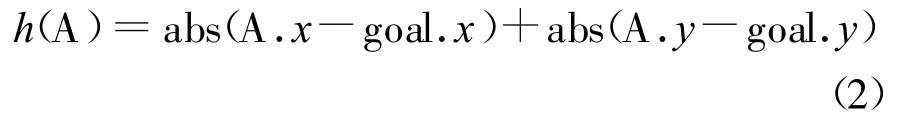
式中,A.x 为当前点的x 坐标值,A.y 为当前点的y 坐标值;goal.x 为目标点的x 坐标值,goal.y为目标点的y 坐标值;h(A)为当前点的Manhattan估计值。

由上式可知,M anhattan 估算函数与当前点到目标点的x 方向距离绝对值及y 方向距离绝对值的和成正比,即具有估算因子的功能,又拥有较高的运算效率。然而,巡视器可以在地图上作斜线方向的运动,故将M ahattan 距离修正为

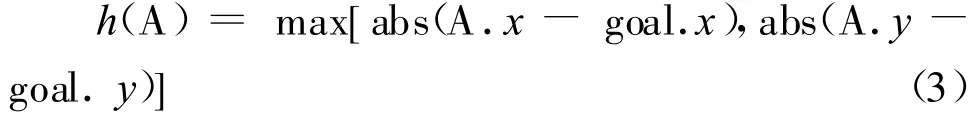
此时,路径会明显分为两个阶段:第一阶段,路径点首先向着靠近目标点斜对角线的方向延伸,当规划的路径走到与目标点斜对角时,路径走向进入第二阶段;第二阶段,路径点以斜向移动快速靠近目标点,这种方法相对于锯齿状移动的路径,消耗大为减少。

此外,本文在A*算法的处理上还做了两个方面的修正。首先,对自排序链表的构建进行了优化,即open 列表在组建时根据f 值大小进行排序, f 值小的排在表头处,使得插入点的排序工作仅在表尾几个节点进行,甚至可能不需要移动任何节点直接将新节点排在表头,不仅节省了运算时间,还有利于保留曾经走过的路径信息。其次,在寻路结束之后,在返回规划路径之前对路径链表进行了优化处理,通过两个指针从路径链表的两端向另一端遍历,寻找出路径链表中的迂回路径,并切除多余部分的路径节点。算法的流程图如图1 所示。总之,改进的A*算法不仅考虑了距离和栅格的可通过性,还提高了路径规划的效率,适合用于非结构化月面栅格地图上的路径规划。

2.3 仿真验证

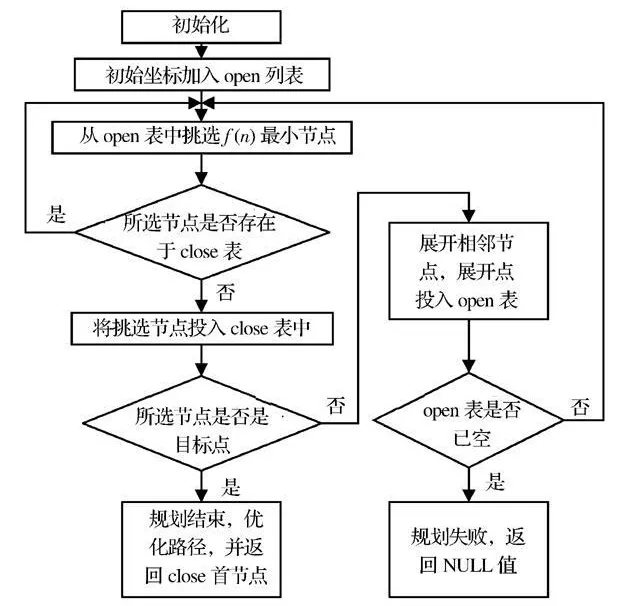
图1 算法流程图Fig.1 Flow chart of arithmetic

采用改进的A*算法,在构建的栅格月面地图上进行路径规划, 如图2 所示。已知单位栅格为10mm ×10mm, 路径的起始点坐标为(140mm,930mm),目标点坐标为(910mm ,150mm),则路径搜索过程耗时1.293s,路径长度为1 381.5mm,满足巡视器的路径规划的需求。

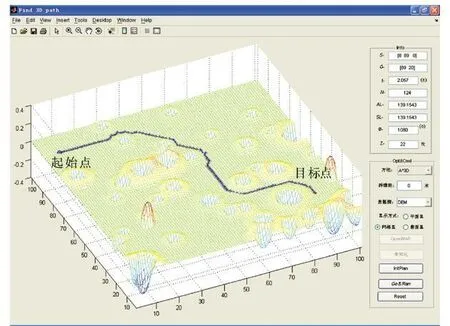
图2 采用改进A*算法的路径规划Fig.2 Path planning using improved A*arithmetic

3 机械臂的路径规划方法

机械臂的路径规划方法(Manipulator Path Planning Method,MPPM)与巡视器的路径规划方法有着本质的不同,巡视器的路径规划受限于地形地貌和巡视器的行驶性能;而机械臂的规划过程受外界的影响一般仅是碰撞检测方面,其余则受限于自身的特性,如工作空间、臂长和构型设计的影响等。

机械臂的路径规划M PPM,首先在机械臂Denavit-Harterberg(D-H)建模的基础上,采用蒙特卡罗法求得机械臂的可达工作空间,然后规划得出机械臂工作空间内的路径点,最后通过运动学逆解计算和关节插值,得到机械臂的运动路径。

3.1 机械臂D-H 建模

巡视器机械臂简化模型如图3a 所示,由三个关节组成。其中,a1=110mm ,指关节1 与关节2 轴线之间的距离;a2=350mm,指关节2 与关节3 轴线之间的距离;a3=110mm,指有效载荷末端到关节3 轴线的距离。

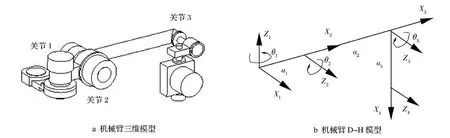
图3 机械臂建模Fig.3 Model of the manipulato r

根据D-H 坐标系建立法则,建立机械臂的DH 模型,如图3b 所示。其中,Z1指关节1 的转动轴线,Z2指关节2 的转动轴线,Z3指关节3 的转动轴线,Z 4 的坐标原点位于有效载荷末端面的中心。机械臂模型的D-H 参数如表1 所示。

表1 D-H参数表Table 1 D-H parameter

由机械臂模型的D-H 参数,求机械臂末端点在x,y,z 坐标系下的位置参数方程为

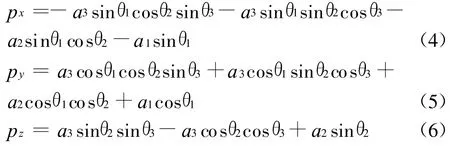
3.2 机械臂可达工作空间分析

机械臂工作空间的求解采用蒙特卡罗法[9]。蒙特卡罗法是一种基于“随机数”的计算方法,属于概率统计方法的一种,同时也具有一般数值方法的优越性。求解机械臂的工作空间时,对关节变量通过均匀分布,赋予一定数量的、符合关节变化要求的随机量,从而得到工作空间由随机点构成的图形,称之为“云图”,这样就构成了机械臂的可达工作空间。求解方法的程序流程图,如图4 所示。

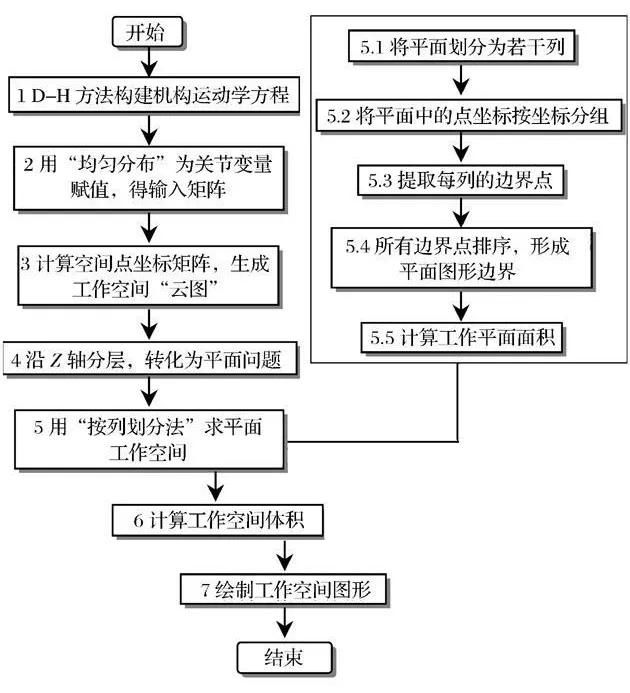
图4 蒙特卡罗方法求解工作空间的程序流程图Fig.4 Flow chart of finding workspace using Monte Carlo method

根据D-H 参数,考虑机械臂的关节空间约束,使用式(4)～(6),采用蒙特卡罗法,对机械臂进行工作空间分析,确定机械臂的可达工作空间如图5 所示。由图5 可以看出,三自由度机械臂的构型对应的可达工作空间为一个带半球空腔的半球体,机械臂与其可达工作空间的关系如图5 a 所示,可达工作空间的两个方向的视图如图5 b、c 所示。

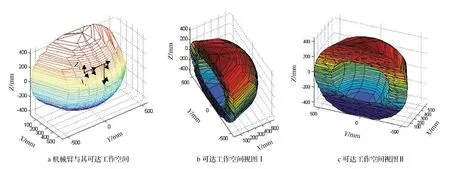
图5 机械臂的可达工作空间Fig.5 Reachable w orkspace of the manipulator

3.3 机械臂的路径规划

在机械臂的工作空间内,根据机械臂的起始点和目标点,确定多个路径段,每个路径段用小直线段表示。

首先,通过运动学反解计算,得出每个路径段内每个关节需要运动的范围,设起始关节角度为θ0,终止关节角度为θf。

然后,使用关节插值计算,本文采用三次多项式插值,可以得出机械臂的运动路径(轨迹)。

每个关节的运动轨迹为

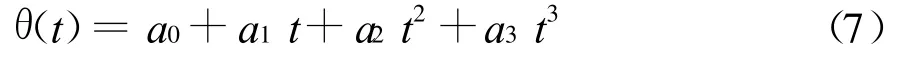
运动轨迹上关节的角速度为

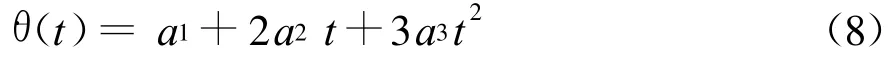
运动轨迹上关节的角加速度为

其中,t 为运动轨道的时间变量, a0=θ0,a1=

这种机械臂的路径规划的方法比较简单、直观,是在计算出机械臂的工作空间的基础上,人为确定路径点,然后通过机械臂运动学计算最终得出其运动路径。此外,可以通过碰撞检测,由机械臂自主确定路径点,完成整个路径规划过程。但是,碰撞检测的设置需要机械臂所处外部环境的精确建模和机械臂本体与外部环境的接触判断,受多方面因素的限制,相对复杂,在一定程度上会影响机械臂的探测效率,故暂不采用。

4 器臂动态联合的路径规划方法

巡视器携带机械臂就位探测时器臂动态联合的路径规划方法(Rover-M anipulator Path Planning M ethod,RM PPM),将上述巡视器和机械臂的路径规划结合起来,巡视器路径规划的目标点和巡视器于目标点的探测姿态,将作为机械臂路径规划的初始点和初始姿态,如图6 所示。整个规划过程描述如下:

首先,确定巡视器路径规划的目标点和巡视器于目标点的探测姿态,使机械臂末端点和探测目标点均处于机械臂的工作空间范围内,如图6 中石块6 处的放大图部分所示;

其次,采用改进的A*算法,在三维栅格数字高程地形图上,进行巡视器路径规划,得出较优的巡视器规划路径,其中,巡视器初始点根据栅格地形确定,目标点为上一步确定的巡视器路径规划的目标点;

再次,于目标点调整巡视器到探测姿态,在调整过程中,有巡视器最佳探测方向的判断,需要精确的求解机械臂的可达工作空间,使机械臂末端点和探测目标点均处于机械臂的工作空间范围内,同时保证巡视器处于最稳定的状态,以免机械臂探测时巡视器出现滑动、倾斜等问题;

最后,在机械臂的工作空间内,确定机械臂的路径点,用小直线段连接,通过运动学反解计算和三次多项式插值计算,得出机械臂的规划路径。

整个路径规划过程之所以称为动态联合,是因为受非结构化月面地形的影响,巡视器于目标点的位姿与初始规划的位姿一般会有较大的偏差,需要根据遥测信息进行修正,才能作为机械臂路径规划的输入。

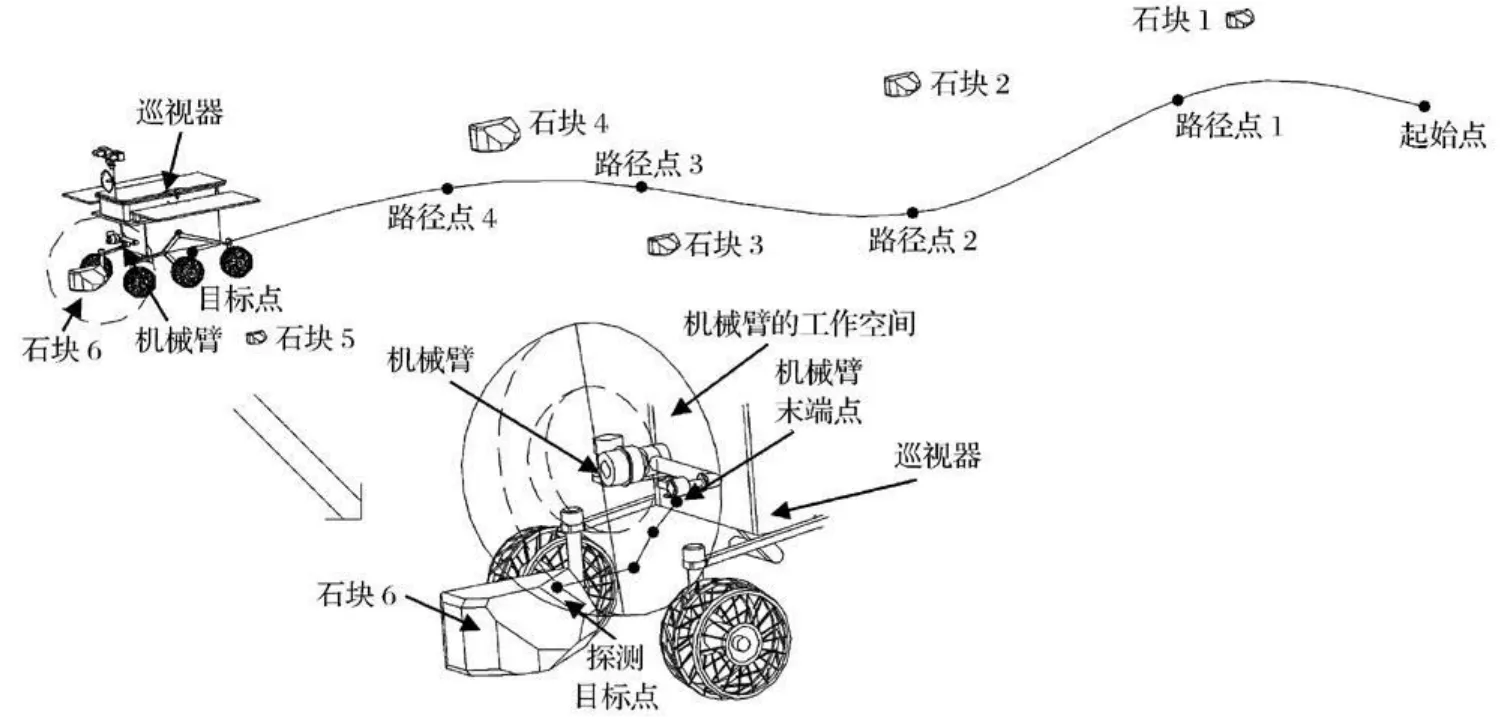
图6 器臂动态联合的路径规划示意图Fig.6 Sketch map of Rover-Manipulator Path Planning

5 结论

综上所述,巡视器的路径规划有两种:一种是针对移动的巡视器的路径规划方法(LRPPM),一种是针对机械臂的路径规划方法(M PPM),两种结合起来(RMPPM),才能够完成就位探测。因此,带机械臂的月面巡视探测器的路径规划方法的研究内容,不仅包括巡视器的路径规划和机械臂的路径规划,还需要完成巡视器携带机械臂就位探测时器臂动态联合的路径规划。

带机械臂的月面巡视探测器的路径规划方法的特点归纳总结如下:

1)巡视器的路径规划过程具有动态性和不完整性。规划方法基于月面三维数字高程图(DEM),采用改进的A*算法完成路径的搜索与择优。

2)机械臂的路径规划仅在自己的可达工作空间内进行,需要针对障碍进行碰撞检测。规划方法基于D-H 建模,采用蒙特卡罗法求得机械臂的可达工作空间,然后人为辅助通过运动学反解计算和三次多项式插值计算,规划得出机械臂工作空间内的运动路径。

3)巡视器携带机械臂完成就位探测的过程,需要上述两种规划的动态联合。实际过程中,还需要地面操作人员的参与,尤其是机械臂初始方位的输入和机械臂到位的判断。

)

[1]叶培建,孙泽洲,饶炜.嫦娥一号月球探测卫星研制综述[J].航天器工程, 2007, 16(6):9-15

[2]Huntsville, Alabama.A brief history of the lunar roving vehicle[R].NASA Marshall Space Flght Center, 2002:3

[3]Joseph Carsten, Arturo Rankin, et al.Global path planning on board the Mars exploration rovers[C]//Aerospace Conference 2007, IEEE, Big sky, MT,2007:1-11

[4]Tunstel E, M aimone M, Trebi O A, et al.Mars exploration rover mobility and robotic arm operational performance[C]// System, M an and Cybernetics, 2005 Internationl Conference on IEEE, 2005:1807 -1814

[5]席裕庚, 陈卫东, 王卫华.基于不确定信息的移动机器人地图创建研究进展[J].机器人, 2001,23(6):563-568

[6]Kambhampati S, Davis L S.M ultiresolution path planning for mobile robot[J].IEEE Journal of Robotics and Automation, 1986, RA2(3):135-145

[7]张颖,吴成东, 原宝龙.机器人路径规划方法综述[J].控制工程, 2003, 5(10):152-155

[8]Sanjiv Singh, Reid Simmons, T rey Smith, et al.Recent progress in local and global traversability for planetary rovers[C]// IEEE International Conference on Robotics and Automation.San Francisco, 2000, 4:1-7

[9]Denavit J, Hartenberg R S.A kinematic notation for lower-pair mechanism s based on matices[J].T rans.ASME, J of Applied Mechanics, 1955, 77(6):215-221

[10]张孝泽.蒙特卡罗方法在统计物理中的应用[M].郑州:河南科学技术出版社,1991