探月飞行的调相轨道

杨维廉

(北京空间飞行器总体设计部,北京 100094)

1 引言

我国的第一颗月球探测器嫦娥一号于2007年10月24日成功发射,并于11月7日进入离月面约200km 的圆形极月轨道,整个飞行过程历时14d。发射嫦娥一号探测器的运载火箭是多次成功发射地球同步卫星的长征-3A, 它所提供的是近地点200km,远地点51 000km 的大椭圆轨道。地月之间的平均距离约384 000km。为了达到这样的距离,嫦娥一号在进入地月转移轨道前经历了一段绕地球飞行的调相轨道,卫星在调相轨道上,利用自身的推进系统进行了三次近地点轨道机动后,进入地月转移轨道。经典的由运载火箭直接将探测器射入地月转移轨道的飞行只需3～5d[1]。

调相轨道(Phasing O rbit)的概念在航天飞行中有着较为广泛的应用。这种概念不像椭圆轨道、双曲线轨道或者地球同步轨道、太阳同步轨道那样有特定的具体内涵,因此很难给出严格的定义。国际上对这个术语的一种解释性的定义是:“进入最终的轨道前所采用的临时性的轨道”(Temporary orbit used prior to injection of satellite into final orbit)。ESA 的一些文献将探月飞行中所采用的调相轨道称为中间轨道(Intermediate Orbit),而美国的一些文献将发射地球同步卫星过程中所采用的中间轨道也称为调相轨道。

在探月飞行中采用调相轨道有两类不同的情况:一类是卫星在运载火箭提供的地球同步转移轨道(G TO)基础上,再经由调相轨道加速到地月转移轨道,嫦娥一号可以归属第一类。这一类的探月飞行方式是1990年代ESA(ESA bulletin 103-August 2000, w ays to the Moon)首先提出的,其创新点在于充分利用运载火箭阿里安-5 发射GTO 的剩余的运载能力搭载月球探测器。所策划的探月计划有M ORO(Moon Orbiting Observatory), LEDA(Lunar European Demonstration Approach), Euro-Moon 2000 和LunarSat (Lunar Academic and Research Satellite)。但是由于种种原因,这些探月计划都未实施。我国的嫦娥一号是成功地按这类调相轨道飞行的首个月球探测器。另一类采用调相轨道的月球探测器并不是因为火箭的运载能力不够,而是要利用调相轨道来减小转移轨道中途修正所需的速度增量,以及扩大发射窗口[2-4]。当然第一类调相轨道同样也可以充分利用这个优越性。本文重点讨论采用调相轨道的这两个优点。

2 地月转移轨道及中途修正

2.1 地月转移轨道

不论是否采用调相轨道,探月飞行的探测器在到达月球前都将经由地月转移轨道,它可以近似地看成是半个大椭圆轨道,非常类似于发射地球同步卫星所采用的转移轨道。表1 给出在讨论中需涉及到的几种轨道的主要特征, 特别是近地点速度。表中的前三条是地月转移轨道,第四条是地球同步转移轨道,最后一条是近地的圆形停泊轨道。

表1 几条转移轨道的主要特征Table 1 Comparison of transfer trajectories

第一条是最典型的地月转移轨道,rp 是近地点的地心距,对应的高度是200km ,ra是远地点的地心距,取为月球轨道的平均距离384 000km。表中所列的轨道平面内所有轨道参数都可以由这两个参数计算出来,a 是半长轴,e 是偏心率,vp是近地点速度。由半长轴a 还可以算出轨道周期, 它是238.6h,约10d,因此卫星在转移轨道上飞行的时间约5d。这条轨道的近地点速度是vp=10.915 5km/s,如果低于这个速度,卫星就飞不到月球附近,所以这条轨道又称为最小能量轨道。

表1 中的另两条地月转移轨道的近地点高度分别是600km 和1 200km,相应的近地点速度分别是10.584 5km/s 和10.360 0km/s, 这说明近地点速度与其高度密切关联。

为了达到所需的近地点速度,必须采用多级火箭,经典的做法是先使得探测器进入一个近地的圆形停泊轨道(参见表1 的最后一行),然后进行轨道机动,将速度提升到所需大小。对于本文的例子所需的速度增量是Δvp=3.131 3km/s。通常有两种做法来提供这样大的速度增量,一种是采用固体火箭,在这种情况下,探测器可以根据需要,在停泊轨道上运行若干圈,然后选择恰当时机进行轨道机动;另一种是采用液体火箭末级两次点火的办法,火箭携带探测器进入近圆形的停泊轨道,运行一段时间后,通过末级火箭再次点火来提供进入地月转移轨道所需的速度增量,嫦娥一号所采用的运载火箭长征-3A 就是这种类型。

经典飞行方式的最大优点是从地球飞到月球所需的时间最短,这对载人探月明显是十分有利的,在早期的阿波罗计划中一般都飞行约3d 的时间。但这种飞行方式对发射窗口的要求比较严格。

发射窗口包括“发射机会窗口”和“发射时间窗口”两部分[4],发射机会窗口是指连续可发射的日期,发射时间窗口是指每个发射日期内可发射的时间间隔。月球在不同日期的位置有很大的差别,不同日期发射的弹道也应该不同。

2.2 中途修正

由于地月转移轨道的飞行时间比较长,进入转移轨道时的微小误差在到达月球时也会变得很大,因此在飞行过程中需要进行轨道的中途修正。

我们在解算地月转移轨道时的具体做法是,根据对到达月球时刻tf的三个终端条件(q1,q2,q3)来求解卫星在t0时刻位于近地点时的三个参数(vp,Ω,ω)值,而近地点高度h、倾角i 是已知的,如果实际的轨道与所解算出的标称轨道完全一致,则探测器将准确无误地按这条轨道飞行,并在时刻tf到达月球且满足三个终端条件[5]。探测器在飞行的任何时刻都有相应的位置r 和速度·r,如果在t0时刻探测器的位置和速度有误差,则在整个飞行过程都将偏离标称的轨道。很明显我们在任何时刻都无法将探测器拉回到原来的标称位置,中途修正的做法是根据对轨道的精确测量,在某适当时刻tm来施加一个速度增量Δ·r 使探测器沿着一条新的转移轨道飞行,但仍然可以要求它在规定的时刻tf到达月球,并满足预先设定的三个终端条件[6]。

中途修正所需的速度增量是由进入地月转移轨道近地点时刻t0的轨道误差决定的,其中主要的是近地点的速度误差。而这个误差就是轨道机动时所产生的误差,机动时的速度增量越大,这项误差就越大。对于经典的飞行方式,进入地月转移轨道时的轨道机动需要的速度增量相当大,约为3km/s,因此中途修正所需的速度增量相当大, 可以超过0.1km/s,这是它的另一个缺点。如果采用调相轨道,就可以使得这一次轨道机动所需的速度增量大大减小,进而减小残余误差,这就是调相轨道可以减小中途修正速度增量需求的道理。

3 调相轨道的应用

从上世纪90年代开始的新的月球探测热潮中,开始采用调相轨道的飞行方式,有代表性的是1994年1月25日美国的克莱门汀(Clementine)月球探测器,日本在2007年9月14日发射的月女神(SELEN E)探测器,以及我国的嫦娥一号。这一类飞行轨道的共同特点可以用N +1/2 来表示,就是在飞行器到达月球以前,都将先绕地球运行N 整圈,再进入半圈的地月转移轨道。

3.1 Clementine 的调相轨道

Clementine 是先由运载火箭大力神-IIG 送入高度为276km 的近圆停泊轨道,在这条轨道上运行若干天后,再由固体火箭Star-37 进行加速,使其实现向月球的飞行。飞行轨道模式是2+1/2, 原先设计的是10d+10d+5d,共25d,在5d 的地月转移轨道之前,先在周期为10d 的调相轨道上运行两圈。实际发射时的飞行轨道有较大的变化, 改成3d+10d+5d,共18d,这是因为探测器的质量增加使得固体火箭提供不了所需的3.113km/s 的速度增量,而只能提供3.003m/s 的速度增量,故第一圈的周期由10d 降为3d。等探测器再次运行到近地点P1时,再做一次机动, 将周期增加到10d, 所需要的110m/s 的速度增量由探测器提供。调相轨道第二圈结束后再次到达近地点P2时,只需再做一次微小的调整后,就可以在5d 的地月转移轨道飞行过程中不需要进行中途修正。

这种飞行方式可以增大发射机会窗口的原理是很简单的,就是将两次近地点机动的总的速度增量在P1,P2点进行恰当的分配,具体要求是使得P2点机动后探测器要进入飞行时间5d 的地月转移轨道,而P1点机动后的周期是(10-K)d,K 是发射延后的天数。因此最多可以延后7d,在延后7d 的这种情况,不在P1点机动,只在P2点机动。

3.2 SELENE 的调相轨道

日本的“月女神”计划经过一拖再拖以后,终于在2007年9月14日成功发射。长期以来他们一直是考虑采用H-IIA 运载火箭直接将探测器发射到地月转移轨道,并安排了两次中途修正,对速度增量需求的几次估计都大于120m/s。但最后实际发射采用的方式与Clementine 的方式基本相同,也是2+1/2 的模式,具体的飞行时间是5d+10d+5d,共20d,10月4日才进入月球捕获阶段。运载火箭所提供的绕地飞行的椭圆轨道的近地点高度281km,远地点高度232 800km ,周期是4d23h33min。这条轨道的近地点速度比直接飞到月球附近的转移轨道的近地点速度只差约50m/s。因此采用这种飞行方式应该不是运载能力不够的原因,而是要充分利用调相轨道的优越性。在约20d 的飞行过程中,一共进行了5 次轨道机动:第一次是在9月15日星箭分离后约一天,目的是修正运载火箭误差引起的轨道平面的误差;第二次是在9月16日探测器到达远地点时,主要为了增加近地点的高度;第三次是在9月19日到达近地点时做的一次大的机动,目的是使轨道周期达到10d,也就是使远地点到达月球轨道的距离,这虽然是一次大的机动,但速度增量顶多也就是50m/s 左右;第四次是在9月20日,是对上一次结果的修正;最后一次是在9月29日探测器即将飞离地球的转移轨道近地点的精确修正,此后,一直到10月4日到达近月点这5d 的转移轨道飞行中,未进行任何的中途修正。

关于SE LENE 轨道飞行方面的较详细的公开技术资料还未见到,也没有看到关于发射窗口方面的论述,但按Clementine 的同样道理,采用这种飞行方式,连续发射的机会可以有6d。

3.3 嫦娥一号的调相轨道

嫦娥一号探测器的调相轨道属于第一种类型,探测器是以超GTO 作为停泊轨道,然后用自身的推进系统将轨道转变为地月转移轨道,长征-3A 火箭提供的超GTO 的近地点高度是200km,远地点高度是51 000km ,周期是15.8h。为了到达月球附近,探测器还需要提供约0.5km/s 的速度增量。为了尽量减小重力损耗,需将这样大的速度增量分若干次近地点机动来实现。故采用的飞行轨道模式是7+1/2,即在飞离地球前绕地球运行7 圈。表2 给出调相轨道主要参数及轨道机动的速度增量。地月转移轨道的飞行时间是114h。

表2 嫦娥一号调相轨道主要参数及轨道机动的速度增量Table 2 Phasing orbits and velocity increments for maneuvers

嫦娥一号调相轨道与美国的Clementine 及日本的SELENE 的最大不同点是运载火箭提供的轨道最远只能到51 000km,离月球轨道384 000km 的距离还相距甚远,需要增加的速度超过0.5km/s,而美国和日本的分别是0.1km/s 和0.05km/s。因此我们的轨道机动需要从周期16h 变到24h、变到48h、再变到转移轨道,要进行三次大的近地点轨道机动,而美、日都只要进行一次大的机动。在16h 周期的轨道上运行3 圈的安排,是使进行第一次大的轨道机动的近地点,尽可能与星箭分离点位于同一位置,因为我们需要使用测量船来执行测控任务。安排在24h 周期的轨道上运行3 圈,是保证连续3d的发射窗口,正常的情况是运行3 圈,推迟1d 发射就运行2 圈,推迟2d 发射就只运行一圈。

由于进入地月转移轨道的最后一次轨道机动,只需要约0.2km/s 的速度增量,执行后的绝对误差比较小,大大地减轻了中途修正的负担,嫦娥一号只作了一次很小的中途修正。

4 后期探月仍采用调相轨道的初步讨论

对于我国后续的探月飞行任务,目前初步的设想是改用运载火箭直接将探测器送入地月转移轨道的飞行方式。采用这种方式的最大优点是可以缩短飞行时间,但也有其明显的不足之处:一是由于运载火箭较大的入轨误差,必须在地月转移飞行的中途由探测器自身修正,所需的速度增量比较大,而且一般情况都至少需要修正两次;二是延后日期发射需用不同的发射轨道,这将使地面测控系统的任务更加复杂。因此采用调相轨道这种国际流行的做法也应该作为一种备选方案加以研究。

地月转移轨道的飞行时间现在还未做出最后的选择,但这并不影响问题的讨论,我们可以先以飞行时间为5d(120h)的最小能量地月转移轨道为例来讨论。由于运载火箭已经有足够的能量达到所需的速度, 这类飞行方式的调相轨道的通用模式是2+1/2的模式,即在进入地月转移轨道前,只安排探测器绕地球飞行两整圈。具体的轨道周期按K d+10d+5d 考虑,K 应该小于等于10。美国的Clementine 原先的方案K =10,实际发射时改为K =3;日本的SELENE,K =5。

K 值的选择要兼顾扩大发射窗口及节省探测器的能量两方面来考虑,选K =10 理论上讲,就是靠运载火箭直接将探测器发射到与月球交会所需的距离,这种选择在发射日期需要延后时,只能靠改变运载火箭的发射弹道来解决。如果选择K ＜10,就可以在延后发射时不改变原定的发射弹道,而只需要探测器再做一次近地点轨道机动,增加一点的速度增量就能进入原定的地月转移轨道。表4 给出对应不同K 的轨道参数, 以及探测器将其变成周期10d 的轨道所需额外提供的速度增量(最后一列)。图1 的曲线显示这个速度增量随发射轨道周期的增加而显著地减小。

表3 对应不同K 值的轨道参数及所需的近地点速度增量Table 3 Requirement of velocity increments at perigee

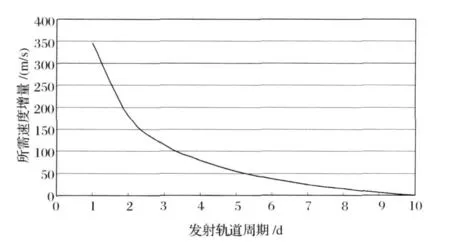
图1 探测器所需提供的速度增量与发射轨道周期的关系Fig.1 Velocity increments vs.launching orbital period

如果选取K =3,这就是美国Clementine 的情况,运载火箭将探测器只送到周期为3d 的轨道,探测器还需要靠自身的推进系统提供115m/s 的速度增量,才能飞到月球附近,这实际上和中途修正所需消耗的速度增量差不多。

如果选取K =4,则探测器还需要79m/s 的速度增量。

如果选取K =5,对应的是日本SELENE 的情况。探测器只需再提供55m/s 的速度增量,就可以飞到月球附近,这比不采用调相轨道由运载火箭直接送到月球所需的中途修正的速度增量还要小很多。

对于我国的情况,为了尽可能充分利用运载火箭的能量,并能够达到像嫦娥一号保持连续3d 的发射机会,可以选择K =8。标称的飞行模式为8d+10d+5d,即由运载火箭将探测器送到周期为8d 的椭圆轨道,飞行8d 返回到近地点时,探测器做一次轨道机动。这时仅需15m/s 的机动,就可以将探测器送入周期为10d、远地点达到月球距离的大椭圆轨道。10d 后再次回到近地点时,进行一次非常小的轨道修正,就可以进入5d 的地月转移轨道。

如果发射推迟一天,仍然可以采用同样的周期为8d 的发射轨道,所不同的是第一次近地点机动将轨道周期变成9d,所需的速度增量是8m/s。等探测器再次回到近地点时,再做一次速度增量为7m/s的小机动,将探测器送入同一条5d 的地月转移轨道。

如果发射推迟2d,还可以采用同样的周期为8d的发射轨道,探测器在这条轨道上连续运行两圈共16d,等其回到近地点时, 做一次速度增量仅为15m/s 的机动,就可以将探测器送入同一条5d 的地月转移轨道。

对于地月转移轨道飞行时间小于5d,例如嫦娥一号114h 的情况,最后一整圈的周期应该选为9d。标称的飞行模式是7d+9d+114h,做两次近地点机动;若第二天发射改为7d+8d+114h,同样做两次近地点机动;若第三天发射改为7d+7d+114h,只做一次近地点机动。三种情况所需总的速度增量都是25m/s。

)

[1]杨维廉,周文艳.嫦娥一号月球探测卫星轨道设计[J].航天器工程, 2007,16(6):16-34

[2]Dunham D, Jen Shao-Chiang J, Vesugi K, et al.A lanuch window study for Geotail's double lunar swingby trajectory[C]// IAF Paper 90-309, October, 1990

[3]Uesugi K, Matsuo H ,Kawaguchi J,et al.Japanese first double lunar swingby mission—H iten[C]// IAF Paper 90-343, October 1990

[4]Carring D, Carrico J, Jen J, et al.Trajectory design for the deep space Program Science Experiment(DSPSE)mission[R].AAS 93-260,1993

[5]杨维廉.发射极月卫星的转移轨道研究[J].航天器工程,1997, 6(3):19-33

[6]周文艳,杨维廉.月球探测器转移轨道的中途修正[J].宇航学报,2004, 25(1):89-92