近Leibniz流形的判定及应用
2010-01-06张福娥赵晓华
张福娥,曾 辉,赵晓华
(1石河子大学师范学院数学系,石河子832003;2新疆教育学院,乌鲁木齐830054;3浙江师范大学数理信息工程学院,金华321004)
近Leibniz流形的判定及应用
张福娥1,曾 辉2,赵晓华3
(1石河子大学师范学院数学系,石河子832003;2新疆教育学院,乌鲁木齐830054;3浙江师范大学数理信息工程学院,金华321004)
为进一步完善近Leibniz流形的理论,从张量的角度研究了Leibniz流形及近Leibniz流形,给出了Leibniz流形的张量表示形式,并用该张量形式表示了Leibniz流形和近Leibniz流形上的动力系统,然后给出一个近Leibniz流形是Leibniz流形的判定条件,且把它应用在近Leibniz动力系统上。
Leibniz流形;近Leibniz流形;近Leibniz动力系统
众所周知,典则的 Poisson括号{·,·}有5个重要性质[1,2]:双线性、反称性、导性(Leibniz法则)、Jacobi恒等式和非退化性。经典力学大多是用Poisson括号描述的。一个流形的Poisson括号是一个双线性映射,这个括号定义了 C∞(M)上的一个李代数结构,且它满足导性,这使得流形 M上的光滑函数决定了Hamilton向量场 Xh,Poisson括号的导性在 Xh对应的动力系统中起着非常重要的作用。为了不受偶维数的限制,或研究更一般的系统,人们做了许多推广和努力。比如去掉非退化性限制引进广义 Poisson括号,研究广义 Hamilton系统[3]。
Leibniz括号[4]是广义 Poisson括号的推广,为更一般的系统提供了几何模型[4~7],它满足双线性和Leibniz法则,而去掉了反称性,由此定义的动力系统一般与经典的 Hamilton系统不同。Weinstein[8]在拉格朗日力学及群胚中研究表明,相关的动力系统可描述为一个光滑函数和括号的向量场,这样定义的结构仅要求线性和对每个元具有导性,这也是西方把此类括号称为Leibniz括号的原因。
近Leibniz括号也是按此定义的,它是Leibniz括号的一种推广。近Leibniz括号只要求满足线性和左导,而不满足右导性,故它能为非交换的的非线性系统提供更广泛的模型。本文从此角度出发,给出近Leibniz流形是Leibniz流形的一个判断条件,并将其应用在动力系统上。
1 预备知识
定义1[4]设 M是一个光滑流形,M上的Leibniz括号是一个双线性映射:{¨,}∶C∞(M)×C∞(M)→C∞(M)满足

其中 f,g,h∈C∞(M),把(M,{¨,})称为 Leibniz流形。
定义2[4]设(M,{¨,})是Leibniz流形,h是 M上的光滑函数,在 M上存在2个向量场和满足(f)={f,h},(f)={h,f},∀f∈C∞(M),把称为 Hamilton函数h对应的右Leibniz向量场,称为 Hamilton函数 h对应的左Leibniz向量场。

括号[·,(·,·)]满足左导称为近Leibniz括号,(M,p,g[·,(·,·)])称为近Leibniz流形。可知近Leibniz流形满足双线性,这里只需令 h是常数即可。
2 定理及证明
张量在研究Poisson流形及辛流形时具有重要的作用,同时它在Leibniz流形及近Leibniz流形的研究中也具有重要作用。下面先给出Leibniz流形上的张量形式,然后从张量的角度研究Leibniz流形及近Leibniz流形的一些性质。
定理1:流形 M是Leibniz流形的充分必要条件是:其上有一个二阶逆变张量π,其二阶逆变张量可以表示为:

证明:设(xi),i=1,2…n是Leibniz流形 M上的局部坐标,则对∀f,g∈C∞(M)有:

由于结构矩阵(Mij)是唯一的,故Leibniz括号{·,·}唯一确定了 M上的一个张量
π(d f,d g)={f,g}。反之,若流形 M有一个二阶逆变张量π,π在局部坐标下表示为

先证明{·,·}是Leibniz括号。
由于π是张量,故

类似可证

再证其唯一性。
若存在

故{·,·}1={·,·},即 M上的一个二阶逆变张量π唯一确定了M上的一个Leibniz括号。
由上所述,流形M上的一个二阶逆变张量π与M上的一个Leibniz括号有一一对应关系。故Leibniz流形(M,{·,·})也可表示为(M,π)。
由上可知,可以从张量及括号的角度讨论Leibniz流形及近Leibniz流形上的动力系统。类似于哈密尔顿动力系统,Leibniz流形 M上的动力系统可以表示为:
xi={xi,h}。
由定理1知:
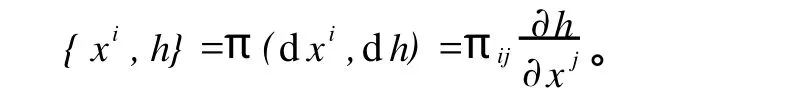
若设(xi)i=1,…,n是流形M上的局部坐标,由定义3知近系统由 ˙xi=[xi,(h1,h2)]给出,其中[xi,(h1,h2)]=。特别是,若 p为一个反称的(2.0)型张量场,g为对称非退化的(2.0)型张量场,此时近Leibniz括号为近度量括号,可表示为:
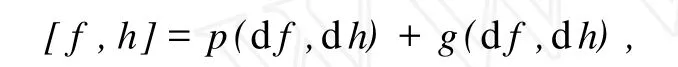
而它所对应的动力系统为:

下面给出近Leibniz流形与Leibniz流形的一个关系,并举例说明其在动力系统上的应用。
定理 2 对于定义 3中的近括号[·,(·,·)],若(h,h)=h,则 [f,(h1,h2)+(h2,h1)]是Leibniz括号,其中∀f,h1,h2,h∈C∞(M)。
证明:对

推论:对于定义 3中近括号[·,(·,·)],若(·,·)可换,且 (h,h)=h,则[·,(·,·)]是Leibniz括号,且 p=g。反之,若近Leibniz中 p=g,(h,h)=h,则(·,·)可换,且[·,(·,·)]是Leibniz括号。
证明:若(·,·)可换,且(h,h)=h,由定理 2知,[·,(·,·)]是括号,此外

由 f,h1,h2的任意性知 p=g。反之,若 p=g且(h,h)=h,显然,(·,·)可换,且[·,(·,·)]是Leibniz括号。
例 设(xi)i=1,…,n是近Leibniz流形 M上的局部坐标,p,g为M上两个二阶张量的结构矩阵,其中 p为奇异反对称矩阵,g为奇异的对称矩阵,

则由 p,g决定的近Leibniz系统为

(1)若(h,h)=h,则定理2中的近Leibniz括号[f,(h1,h2)+(h2,h1)]对应的动力系统为

故此近Leibniz系统具体表示为

(2)由推论知若(·,·)可换,且(h,h)=h,

其对应的近Leibniz动力系统为
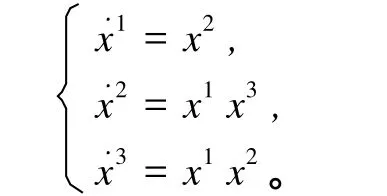
3 结语
近Leibniz流形作为Leibniz流形的推广,为非线性的非交换系统提供了更广泛的几何依据,而讨论近Leibniz流形与Leibniz流形的关系将是研究近Leibniz流形的一个有效的方法。这部分理论有待于进一步研究,并可以延伸到Leinbiz代数胚内容,它的研究为非线性问题及几何理论的发展都有着重要的作用。
[1]贺龙光.辛几何与泊松几何引论[M].北京:首都师范大学出版社,2001.
[2]柯歇尔,邹异明.辛几何引论[M].北京:科学出版社,1986.
[3]李继斌,赵晓华,刘正荣.广义哈密顿系统理论及其研究[M].北京:科学出版社,1997.
[4]Ortega J P,Bielsa V P.Dynamics on Leibniz manifolds[J].Journal of Geometry and Physics,2004,(52):1-27.
[5]Guha P.Metrplectic struture,Leibniz dynamics and dissipative systems[J].Math Appl,2007,(326):121-136.
[6]王宝勤,张福娥,赵晓华.关于L流形的一些讨论[J].数学进展,2009,6(3):359-366.
[7]张福娥,曾 辉.L流形上函数等价类的性质[J].石河子大学学报(自然科学版),2008,26(5):658-660.
[8]A Weinstein.Lagrangian Mechanics and groupoids[J].American Mathematical Society,1996,(7):207-231.
Judgement and Application of Almost Leibniz Manif olds
ZHANG Fu'e1,ZENG Hui2,ZHAO Xiaohua3
(1 Department of Mathematics,Teachers'College,Shihezi University,Shihezi 832003,China;2 Xinjiang Educational Institute,Wulumuqi 830054,China;3 School of Maths-Physics,Information and Engineering Science,Zhejiang Normal University Jinhua 321004,China)
To perfect the theories of almost Leibniz manifold profoundly,Leibniz manifold and almost Leibniz manifold are studied f rom point of tensor,and the forms of tensor of Leibniz manifold are given,so dynamical systems on Leibniz manifold and almost Leibniz manifold can be given according to tensors.Then a qualification that almost Leibniz manifold is a Leibniz manifold is given,finally apply it to almost Leibniz dynamical systems.
Leibniz manifold;almost Leibniz manifold;almost Leibniz dynamical system
O186.1
A
1007-7383(2010)01-0121-04
2009-08-19
国家自然科学基金项目(10872183)
张福娥(1980-),讲师,从事微分几何及其应用的研究,e-mail:zhangfue@shzu.edu.cn。
