经典回归与稳健回归方法的应用比较研究

郭亚帆,杜金柱

(1.内蒙古财经学院 统计与数学学院,内蒙古 呼和浩特 010051;2.内蒙古财经学院 教务处,内蒙古 呼和浩特 010051)

经典回归与稳健回归方法的应用比较研究

郭亚帆1,杜金柱2

(1.内蒙古财经学院 统计与数学学院,内蒙古 呼和浩特 010051;2.内蒙古财经学院 教务处,内蒙古 呼和浩特 010051)

本文首先给出基于传统统计方法的经典回归方法中存在的一些不足,然后提出稳健回归方法的应用并通过实证计算与经典回归进行对比分析,最后对两种回归方法进行应用总结,得出稳健回归方法在抵御数据中的离群值方面具有最小二乘回归所无可比拟的优越性的结论。但是由于稳健统计方法通俗性比较差,使得经典统计方法的地位始终无法动摇。因此,在实际运用中,尽可能综合使用经典的和稳健的统计方法,从而达到既能够准确掌握问题主体部分的信息,同时又不会忽略对非主体信息的充分挖掘。

稳健统计;离群值;OLS回归;稳健回归

一、问题的提出

统计学作为一门应用性很强的工具性学科,其目的或任务是从众多数据中挖掘有用的信息,然后得出有关这个领域的某些特征或结论,进而用以指导实践,来“创造”更好的数据。统计的结果一方面依赖于观测数据,另一方面依赖于对所研究总体某些特性的假设,如分布形式,独立性等等。稳健统计学旨在克服当数据显著偏离假设时传统统计学所面临的一些困难,所针对的是统计学中一个普遍而实际的问题,这套方法无论是对科学研究还是对相关部门经济政策的制定都有着重要的理论意义和现实意义。

“稳健”一次来源于英文“robust”,愿意是强壮、健康、坚韧、能经受得住逆境的考验,也有人用汉语谐音将其译为“鲁棒”。[1]稳健统计实质上就是传统统计方法的稳健化。我们知道,在应用传统的统计方法解决实际问题时,收集数据是进行统计分析的基础。然而在获取数据过程中,往往会出现一些未被注意或难以觉察的意外情况。例如实验或生产条件(包括原材料、实验设备、工艺流程等)的突然变化,测量仪表的某种故障,操作人员在记录和抄写中的失误等等,都会使数据出现或多或少地异常的数据,我们称之为异常值,或极端值、离群值(outlier)。①以上各种情况产生的异常值是不正常的,也就是错误的。实际数据中有时还会存在正常的异常值,即实实在在的数据。而且,如Hampel(1977)②指出,实际数据中含有10%左右的过失误差(即通常所说的离群值)是常见的事。由于很多传统的统计方法对离群值非常敏感,因此在传统统计方法下,数据中含有少量离群值可能会对分析结果产生破坏性的影响,甚至导致完全错误的统计结论,这也就使一些经典的统计分析变得毫无价值。在简单的或者是一维数据情形下,我们可以利用一些准则和方法识别出数据中的离群值,从而达到尽量使数据的实际分布与假定模型相吻合,以使经典统计方法仍然具有比较理想的性能表现。但在高维情形,由于无法图示和离群值之间的Mask效应等原因,很难凭直觉或统计方法来判断哪些数据是离群值。经典的统计方法在这些场合将不再适用,它们需要稳健化才能更好地反映真实情况。

传统的线性回归分析,是建立在最小二乘法的基础之上的。最小二乘法要求误差项是相互独立、服从正态分布、以零为数学期望并有相同方差的随机变量。当实际的观测值包含异常值时,误差将不再服从正态分布,而是重尾分布(long-tailed distribution)。对这样的数据作回归分析时,回归直线将是主体数据与异常值之间的一个妥协,而与真实的回归线相差较远,也就是说,这样估计出的参数是不准确的。而稳健回归就能够克服最小二乘回归因离群值而失真的缺陷,得出更为接近实际值的估计。

二、数据中的离群值对线性回归结果的影响

上文已提及,离群值的出现既有主观上的原因,也有客观上的原因;既有正常的出现,也有非正常的出现。实践表明,不管是哪种情形,当一个数据集中有10%或者更多的离群值时,我们就有应该怀疑我们所处理的数据的分布形式。[2]在这种情况下,如果还利用我们基于理论分布的统计方法去处理问题,这显然是不合理的,也是没有意义的。换句话说,传统的统计方法对实际分布与假定分布出现偏差很敏感。解决这一问题的方法有两个思路：一是运用合适的算法将数据中离群值识别并加以处理,之后再用传统的统计方法来处理;二是采用对离群值不敏感的稳健的统计方法来描述和说明数据。在实际运用当中究竟要采取哪种思路,这要看研究者的目的是什么。如果只想得出尽可能接近实际的结论,就用后一种思路;如果除此之外还想深入了解数据的分布形态,那么采取第一种思路是必要的。因为离群值并不总是有害的,有相当部分的离群值是代表了一些新的亮点,如果对其“视而不见”,我们对好多重要信息就无法把握。当然如果有必要,同时采用两种方法是最佳的。

有关离群值的识别或检验问题,统计学界已经做了许多积极有益的探讨,尤其是对单个变量且样本容量不大时,已有许多较好的检验方法,诸如：t-检验、Dixon检验、Grubbs检验、Nair检验、偏度-峰度检验等,而对多变量、样本容量较大的情况,好的方法不是很多。但由于多变量情形在实际问题中应用更为广泛一些,所以本文以下将重点讨论多变量数据中离群值对线性回归的影响。

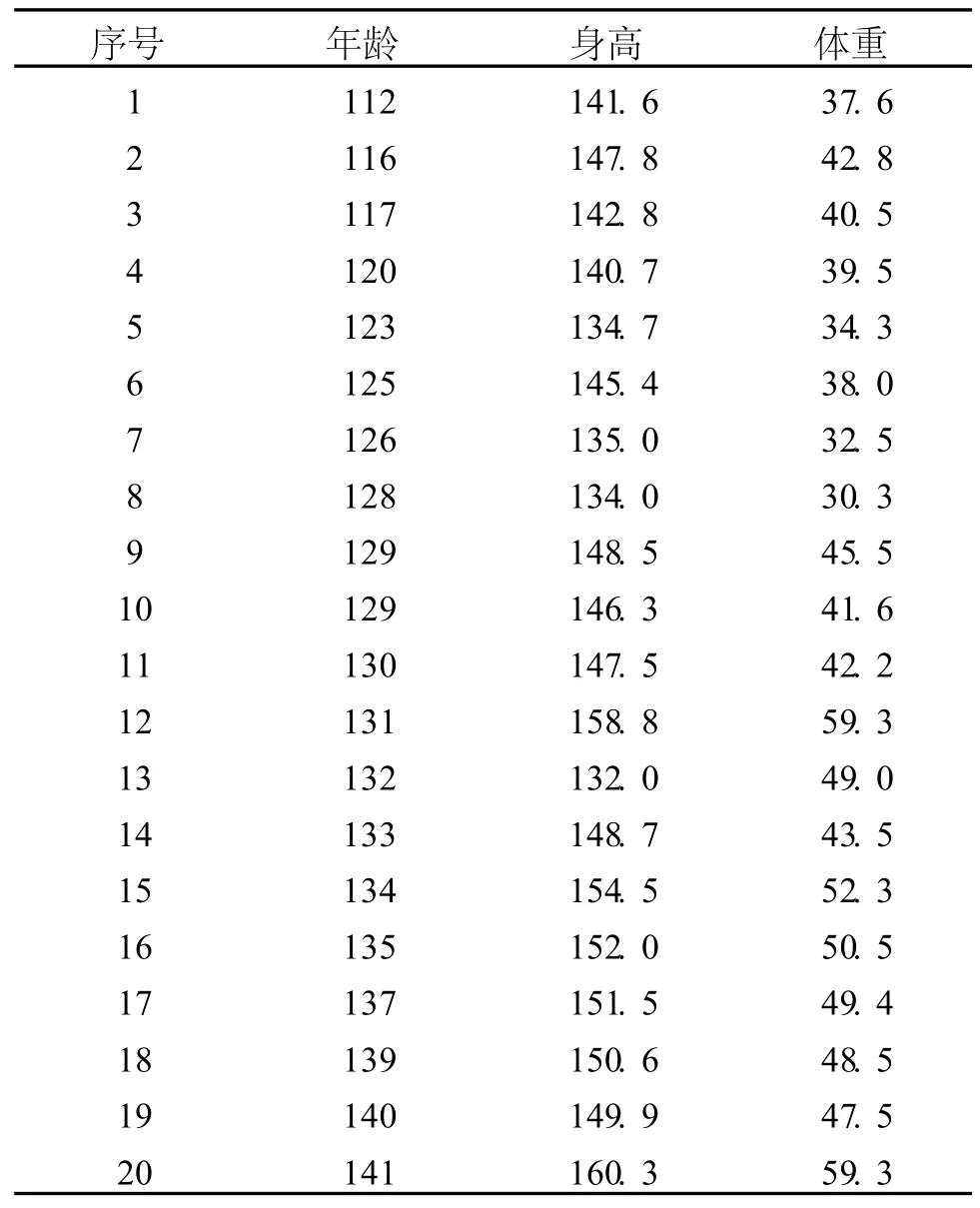
表1 20名学生的年龄(月)、身高(cm)、体重(kg)状况表

在单变量数据中,离群值是以极大值或者极小值出现的,识别起来相对来说要容易一些。但在多变量数据中除了个别变量或所有变量有极端值以外,变量之间相互关系的不协调也会使相应观测量成为离群值。例如表1列出的20名学生的年龄、身高、体重状况,表中第13号数据,年龄：132(月),身高：132cm,体重：49kg。如果不考虑变量之间的关系,而分别分析各个变量,其在各自序列中都不算极端(20号数据体重为59kg,8号数据身高为134cm),但根据常理我们从直观上看,该项记录三个变量之间很不协调,笔者利用统计软件stata8.0中had imvo命令处理,结果显示该项记录的确为离群值。因此多变量数据离群值的识别要比单变量复杂得多,如果不加以处理,会严重影响变量之间包括相关关系在内的各种关系。同样还是上面的例子,如果按照原始数据计算身高与体重的相关系数为0.8147,去掉第13号数据再计算就跃升为0.9713。不仅如此,这样的离群值还会影响相应变量的回归结果,导致不准确或者完全错误的结论,进而造成预测乃至决策的不准确。本文利用呼和浩特市居民实际支出和人均可支配收入的调查数据作回归分析,并比较在剔除离群值前后回归结果以及各项检验统计量的变化情况。[3]

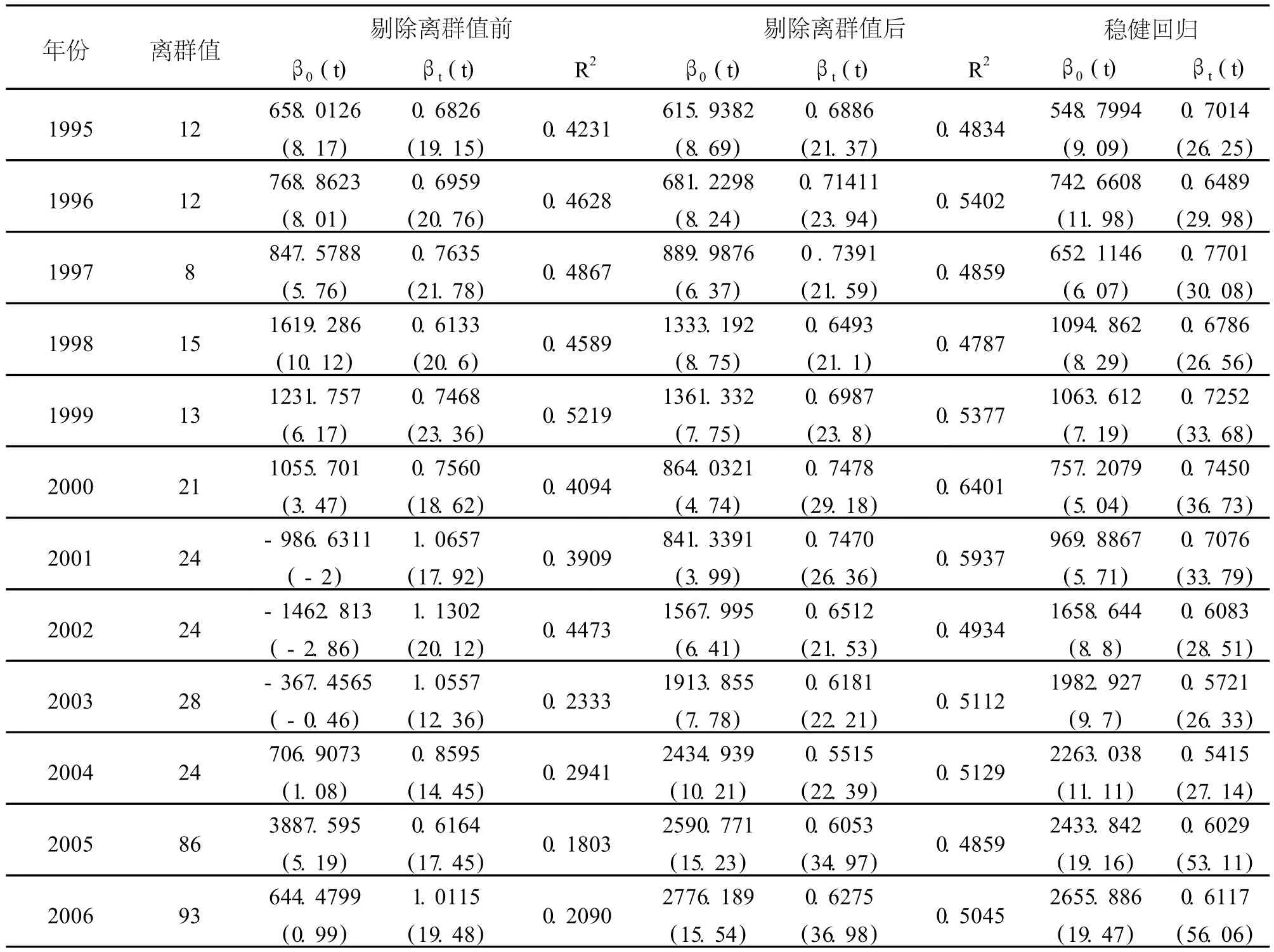
表2 可支配收入与实际支出剔除离群值前后回归结果及稳健回归比较

首先利用原始数据对从1995年-2006年各年份的居民实际支出和可支配收入数据进行普通最小二乘回归分析,然后逐年剔除两个变量中的离群值,之后用剩下的“干净”的数据再次回归。并列表比较。比较结果见表2。观察表2可知,两个变量离群值的数量与分别对单个变量识别的离群值的数量有了很大的变化,这说明多维变量离群值的检测更多的是考虑变量之间的协调关系而非各个变量数值上的极端性质。观察剔除离群值前后回归系数以及系数的t检验统计量和回归可决系数R2我们发现,以上两项重要的检验回归结果的统计量都有不同程度的改善和提高。特别是2001、2002和2003年三个回归结果常数项为负值(分别为-986.6311、-1462.813、-367.4565),消费倾向大于1(分别为：1.0657、1.1302、1.0557,但是t检验都却能通过),已经无法解释其经济意义,有的常数项系数检验通不过,但是在剔除离群值之后的情况：对应常数项(分别为：841.3361、1567.995、1913.855)和消费倾向(分别为：0.7470、0.6512、0.6181)立刻得到质的改变,系数检验都能通过,可决系数也得到很大的提高。对2006年回归结果的影响也很大,常数项和消费倾向分别由644.4799元和1.0115变为2776.189元和0.6275,可决系数由0.209变为0.5045。

通过以上分析我们可以看出多维变量数据中离群值对普通最小二乘回归的影响之大远远超出我们的想像。对于以上四个年度的回归结果,我们尚且尚有理论依据认定这样的结果肯定是错误的(即常数项必须为正,截距项不应该大于1),进而去寻找原因。有些情况我们并没有先验的知识去判断所产生的结果是否合理,而是相反要根据结果去得出结论。这时如果不考虑离群值的影响,其危害性时可想而知的。

三、稳健回归方法的应用

以上分析了多变量数据中离群值对经典最小二乘回归的影响,得出的结论是剔除离群值后的回归结果有很大的改善。但是并不是在所有情况下都能够把离群值识别出来,一是由于实际数据之间的关系往往很复杂,这给识别离群值增加了难度;二是虽然识别离群值的方法有很多,但每种方法都不是尽善尽美的,都有其处理不了或者处理结果不是很理想的情况。就本文提到stata软件中基于Hadi距离的hadimvo命令,我们也不能保证其结果非常理想。因此利用不受极端值影响的稳健回归方法来处理实际问题最能够保证结果的有效性,同时又免去了对处理离群值方法的选择是否合适的考虑。表2后两列是利用stata软件所作的稳健回归的结果。

可见,稳健回归所得的系数与前面剔除离群值之后所得到的结果相差不大,t检验统计量却又有比较大的提高,③这说明稳健回归结果是充分可信的,同时也反映了稳健回归在抵御离群值方面所具有的无可比拟的优越性。

四、对经济指标中经典统计方法与稳健统计方法应用的比较总结

在科研和生产生活领域中,实际数据不符合理想化假定,或出现一些离群值都是无法回避的事实。如果忽视它们的客观存在,就不能保证统计结果的有效性。稳健统计学从理论上论证了经典统计方法的不稳健性,应当唤起我们对经典统计方法缺陷的足够重视。因此笔者认为应该改变过去那种笼统地套用传统统计方法的习惯,将实际数据的预处理(包括数据的统计分布特征、离群值的检验和处理等)作为统计分析中必不可少的第一步。满足应用条件的数据才可以运用经典的统计方法处理,否则必定会得出错误的结论。

从前面的分析中我们不难看出,由于居民基本生活指标数据中有离群值的存在,使得类似基于普通最小二乘法这样的传统回归方法在处理这些数据时,其结果都不同程度地受到影响。而进行稳健回归不必考虑数据的离群值问题,一次便可得到比较理想的结果,从而改进了最小二乘法受极端值影响太大的缺点。但是,稳健估计的运算比较复杂,需要首先选取目标函数(ρ函数),然后用迭代法求解。而目标函数以及迭代初值的选取不仅直接影响到估计的稳健性,而且涉及到一些较为复杂的问题,需要进一步作较为深入的研究。尽管有专门的软件可以计算和实现一些稳健的统计方法,但是由于不同软件的算法往往都根据不同的原理设计,其处理结果往往不能够保持很好的一致性,这给实际运用带来一些不便。因此,要想用稳健统计方法取代传统的统计方法是很困难的,也是没有必要的。而我们承认经典统计方法的缺陷,并非就意味着对其的否定。经典统计方法作为一整套应用性很强的工具,已经渗透到经济及社会实际问题研究的各个领域,因此,尽管在一些情况下存在缺陷,但是由于稳健统计方法通俗性比较差,在运用过程中还有一些不确定性,使得经典统计方法的地位始终是无法动摇的。所以,我们在实际运用中,并不提倡单独使用其中的一种,而是尽可能综合使用经典的和稳健的统计方法,从而达到既能够准确掌握问题主体部分的信息,同时又不会忽略对非主体信息的充分挖掘。[4]

[注 释]

① 国内外大多数文献中对这三个概念基本上不做区分,但笔者认为,异常值和离群值应该没有区别,都包含有分析者的主观认识,而极端值就是事实的客观描述,其中并没有主观成分。在不同的分析背景下,有的极端值有时被认为是离群值或异常值,而有的极端值则不是.

② Hampel.F.R.Rejection rules and robust estimates of location：An analysis of some Monte-Carlo results.In“Transactions of the Seventh Pargue Conference and of the EuropeanMeeting of Statisticians”,1977,187-194.

③ Stata结果没有给出可决系数,这是因为R2是对线性回归总体拟合效果的衡量,而稳健回归是一个非线性迭代的过程.

[1] R·L·奥特,M·朗格内克.统计学方法与数据分析引论(第1版)[M].北京：科学出版社,2003.

[2] David C Hoaglin,等.探索性数据分析(第1版)[M]..北京：中国统计出版社,1998：165-178.

[3] 郭亚帆.稳健统计基本理论及其在居民收入与支出指标中的应用研究[D].天津：天津财经大学统计学院,2005.

[4] 孙宪华.稳健统计在经济指标中的应用及其启示[J].现代财经,2003,(12)：36-38.

[5] 郭亚帆.稳健统计及几种统计量的稳健性统计分析[J].统计研究,2007,(9)：82-84.

C81

A

1004-5295(2010)04-0095-04?

2010-07-14

郭亚帆(1977-),女,内蒙古土左旗人,内蒙古财经学院统计与数学学院讲师,硕士,从事数量经济方法在区域经济中的应用、农业竞争力等方面的研究.

[责任编辑：高平亮]