输油管道内油流带电电流的计算

王菊芬，孟浩龙

（航空油料及油料装备检测试验中心，北京 100076）

输油管道内油流带电电流的计算

王菊芬，孟浩龙

（航空油料及油料装备检测试验中心，北京 100076）

通过对紊流扩散系数和轴向流速的合理简化，推导出电荷守恒方程的近似解析解和冲流电流计算公式。该计算公式具有广泛的适用范围，不仅考虑了流体速度、油品电导率和温度对流动带电的影响，而且借助两个被引入的修正量，考虑了管壁粗糙度、油品老化和固/液界面的电化学反应性质等难以量化的因素对流动带电的影响。利用相关文献提供的试验数据对推导的冲流电流计算公式进行验证。结果表明，计算公式能准确预测冲流电流的大小，从而为管道油流带电量的计算提供了一种方便可靠的手段。

输油管道;冲流电流;电荷守恒方程;解析解;紊流

油料管输过程中产生的静电是威胁油料安全储运的主要因素之一，故开展管线油流带电程度的定量分析研究对于正确实施输油作业，保障油料的安全储运具有重要意义。Gavis和Kosman［1-2］基于放电机理推出了适合于紊流状态下低电导率液体介质的冲流电流计算公式;Tanaka等［3］基于对试验数据的分析推出了简洁的经验公式;Abedian等［4］对紊流状态下油流带电量的计算进行了研究，给出了颇具影响力的冲流电流计算公式;Walmsley［5-7］分别对层流和紊流条件下油流带电问题进行了概括性的理论描述;Touchard等［8-10］则应用电化学中“腐蚀”机制来解释油流的起电机制，并给出了层流状态下冲流电流计算公式。上述文献所提供的计算模型往往根据经验而得［3］或含有一些在实际情况下难以确定的变量［4-10］，并且都没有考虑温度和管壁粗糙度对油流带电的影响，因此计算模型的适用范围狭窄。为此，笔者在文献［11］的基础上，推导电荷守恒方程的近似解析解，根据该解析解得到适用范围较广的冲流电流计算公式，并利用试验数据对计算公式的有效性进行验证。

1 电荷守恒方程及其边界条件

假定:流动所产生的电荷密度足够低，对电导率的影响可忽略不计，电导率在整个流场内均匀分布;油流是充分发展的不可压缩流;油品的施密特数Sc足够高以至于紊流扩散系数对紊流核心区内静电荷分布的影响可忽略不计。

从文献［11］知，紊流状态下油中电荷守恒方程可写为

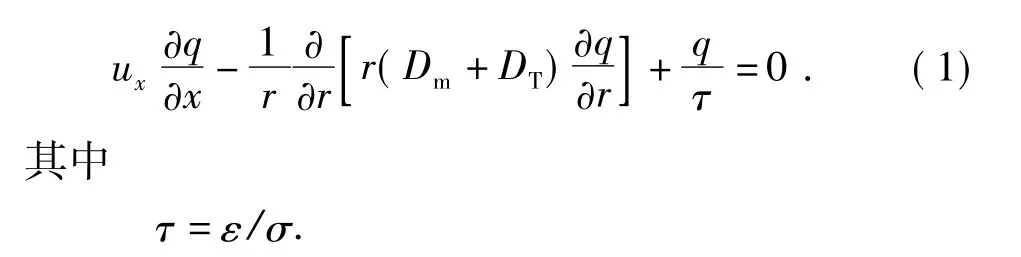
式中，x，r分别为轴向和径向坐标;q为油中空间电荷密度，C·m－3;τ为油品的松弛时间，s;σ为油品电导率，S/m;ε为油品介电常数，F/m;Dm为分子扩散系数，m2/s;DT为紊流扩散系数，m2/s;ux为轴向流速，m/s。

要求解方程（1），必须界定其边界条件。通常管道入口处的电荷密度q0分布已知，这里假定为0，在对称轴上，根据对称性可知∂q/∂若管道足够长，出口处电荷密度已得到充分发展，则可设为管道长度。油/管壁界面边界条件的确定涉及到复杂的油流起电机制。笔者曾基于Gavis J的“放电”机制，提出如下油/管壁界面的边界条件［11］:

式中，R为管道半径，m;F为法拉第常数，C/mol;e为单位电子电量，C;k为玻耳兹曼常数，J/K;T为开氏温度，K;Wσ和WD分别为电导率和分子扩散系数的活化能，J;σ0和D0分别为油品电导率和分子扩散系数以活化能形式表达中的系数项;Um为油流的平均流速，m/s。

除了管壁粗糙度和发生在液/固界面的电化学反应影响油流带电外，油品老化以及油料输运过程中产生的杂质等都会影响油流带电程度。然而，难以找到能定量描述这些因素对油流带电影响的关系式，故引入At和n两个参数来修正，其值可通过试验数据来确定。

2 冲流电流计算公式的推导

2.1 紊流扩散系数和速度

要得到电荷守恒方程的近似解析解，进而得到冲流电流计算公式，必须对方程中的紊流扩散系数DT和轴向流速ux进行简化处理。

Abedian等［4］给出的紊流扩散系数的近似计算公式中充分考虑了圆柱形管道内紊流扩散系数的主要特征，Tourchard等［12］则提供了不同紊流边界层内相应的计算公式。本文进一步对文献［4］的计算公式进行简化，以得到电荷守恒方程的解析解。

在扩散次层内，分子扩散起主导作用，因此和Dm相比，DT可忽略不计。根据文献［4］的计算公式，在扩散次层外紊流扩散系数随着离管壁距离的增加而线性增加，直到在紊流核心区基本上保持不变。本文则将扩散次层外的紊流扩散系数近似为一常数，等于径向上的平均紊流扩散系数，即

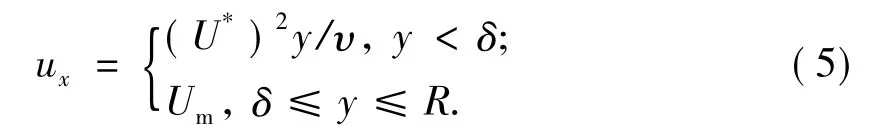
2.2 电荷守恒方程的求解

当油品电导率很低时，即δ/λ≪1，扩散次层内的大量电荷在紊流扩散作用下进入油体内部，紊流区内总的电荷量远远大于扩散次层内的电荷量，因此冲流电流可用平均电荷密度qav来表示，即

对式（1）进行积分，将式（7）代入，整理后得到关于qav（x）的微分方程为

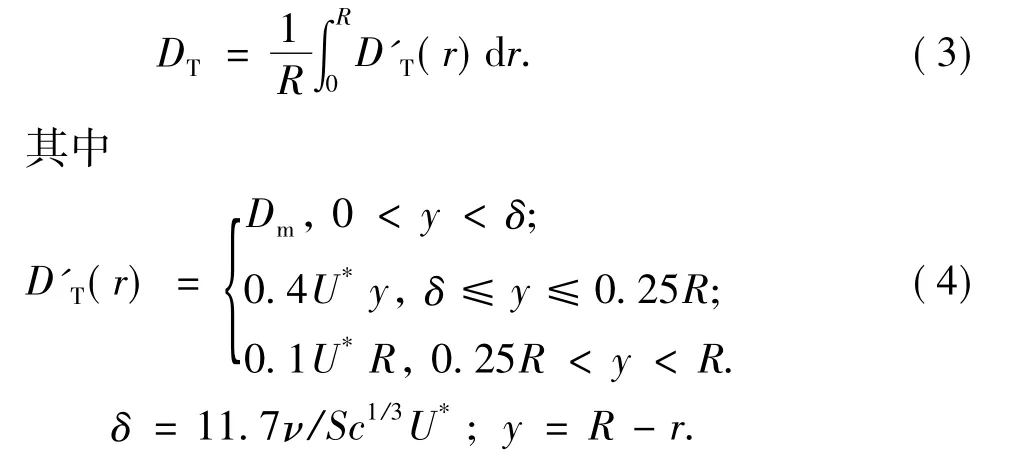
式中，U*为摩擦流速，m/s;δ为扩散次层的厚度，m;ν为油品的运动黏度，m2/s。

因此，DT≈0.0875U*R。这样的近似处理可能会给扩散次层和紊流核心区之间计算区域内的冲流电流预测值带来误差，但对紊流核心区内的影响则可忽略不计，因为在高施密特数下只有管壁附近的紊流扩散系数对电荷分布有重要的影响。

关于轴向流速ux，本文采用文献［4］中的计算公式，即

式中，I∞为饱和冲流电流。

Abedian等的研究表明［4］，冲流电流沿管线方向的变化可近似认为是按式（10）描述的指数规律变化，只是不同电导率范围内饱和冲流电流的计算公式不同。这就涉及到无限长管道出口处电荷守恒方程的求解。此时电荷密度在油中已得到充分发展，电荷密度和x方向无关，式（1）可简化为

在电荷扩散次层，近似采用直角坐标系，对式（12）代入相应的扩散系数，整理后得

式中，λ为德拜长度，用于度量偶电层从固 /液界面向液体内伸展的程度。

求解方程（13），同时考虑边界条件式（2），得

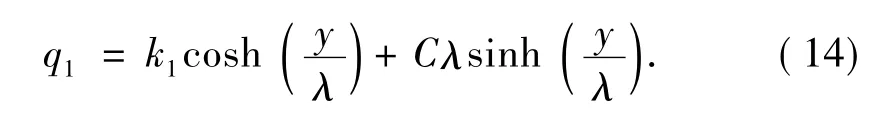
式中，k1为系数。

在紊流核心区内式（12）可写为

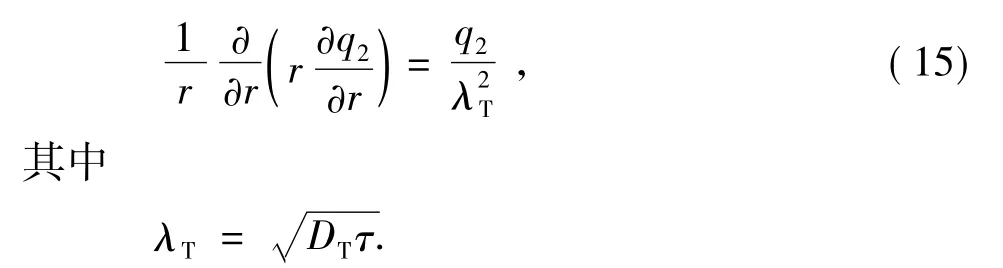
式中，λT为紊流德拜长度。

式中，I0（x）为零阶第一类变形Bessel函数;k2为系数。

k1和k2可根据在扩散次层和紊流核心区的交界面上电荷密度和电场强度必须满足连续性的条件求得，即

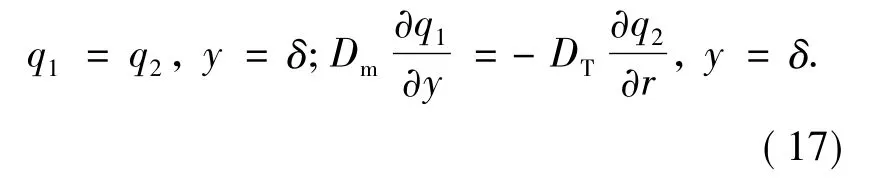
经过一些数学运算，同时考虑到扩散次层的厚度δ远小于管径R，令R－δ≈R，最后得到电荷密度的计算表达式为

对式（18）在管道横截面上进行关于流速的积分，得到饱和冲流电流的计算公式为

式（19）中的前一项代表紊流区内的电荷所形成的冲流电流，后一项代表扩散次层内的电荷所形成的冲流电流。

分析不同的R/λT取值范围下，饱和冲流电流I∞的简化形式。

当R/λT≫1时，根据 Bessel函数性质可知，I0（R/λT） ≈ I1（R/λT），I0（R/λT） ≫ 1，因而可得

由于所研究油品的施密特数比较大，可知λT≫λ，又因为cosh（δ/λ） ≥sinh（δ/λ），式（20） 可进一步简化为

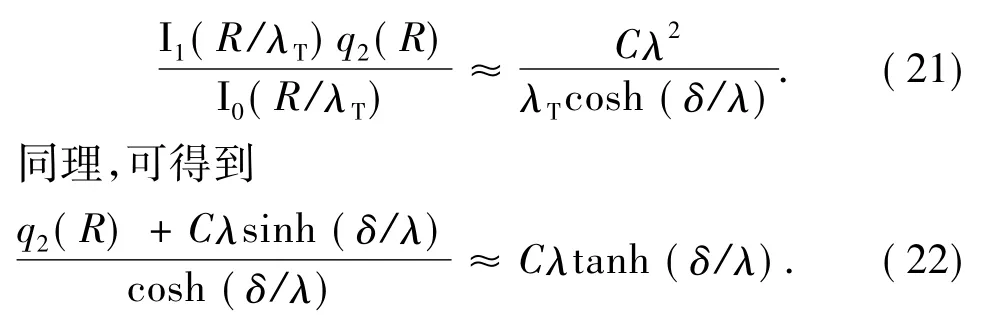
将式（21）和（22）代入式（19），冲流电流的计算公式可简化为

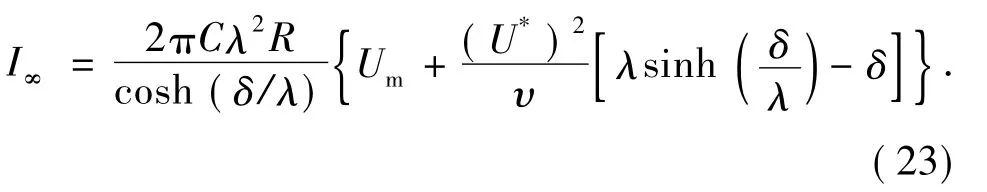
对电导率较高的油品，偶电层厚度远小于扩散次层厚度，即δ/λ≫1，则sinh（δ/λ）≈cosh（δ/λ），λsinh（δ/λ） ≫ δ，而 Um和（U*）2δ/ν处在同一数量级，因而式（23）可简化为

式（24）即为高电导率液体介质饱和冲流电流计算公式。

当R/λT≪1时，在紊流扰动作用下，扩散次层内的大量电荷进入油体内部，故在计算冲流电流时，可忽略扩散次层内电荷对冲流电流的贡献。注意到当R/λT≪1时，δ/λ ≪1。考虑到当 x非常小时，I1（x）≈x/2，sinh（x）≈x，cosh（x）≈1，I0（x）≈1，因此，有

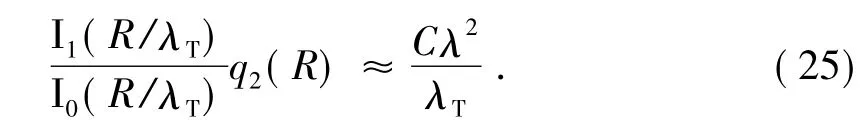
将式（25）代入式（19），则式（19）可简化为式（11）。

对比式（11）和式（23）可知，在条件δ/λ≪1时，式（23）可简化为式（11）。

综上推导过程可知，式（23）适用于所有电导率范围内饱和冲流电流的计算，故若式（11）中饱和冲流电流采用通用计算公式（23），则式（11）具有很强的通用性。

3 计算公式的验证

Tanaka［3］和 Abedian［13］利用试验分别研究了油流速度、油品电导率、油品温度和管壁粗糙度等因素对油流带电的影响，本文中利用他们的试验数据对推导的计算公式有效性进行验证。计算公式中引入At和n的主要目的是修正油品老化、管壁粗糙度等难以量化描述的因素对油流带电的影响，其具体值需要由试验值来确定。为了提高冲流电流预测值的可靠性和准确性，需用参数辨识法来确定At和n的值，计算样本最好从不同工况条件下抽取。当然，采用在线参数辨识将会取得更好的效果。本文采用最小二乘法来估计At和n的值。

Abedian［13］等利用Rutger和Goodfellow 的试验数据对其导出的计算公式进行了验证。由于缺乏相关油品物性参数的具体值，Abedian进行了假设。本文中采用同样的假设值。

图1示出了Rutgers的试验结果［13］和本文计算结果的对比（图中实线为本文的计算结果，各符号点为试验数据），其中，At=37.5，n=0.8。图 2 为Goodfellow的试验结果［13］和计算结果对比，利用参数辨识得到At=20.0，n=1。

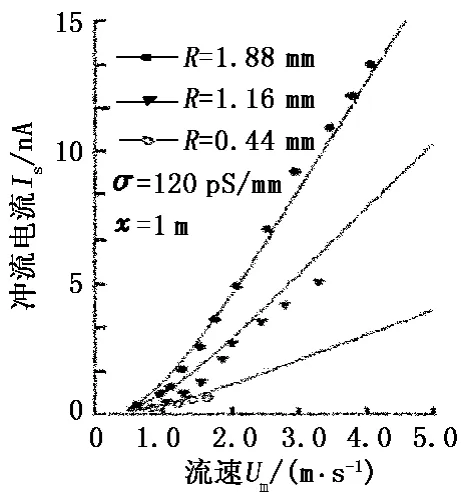
图1 冲流电流和流速的关系Fig.1 Dependence of streaming current on velocity

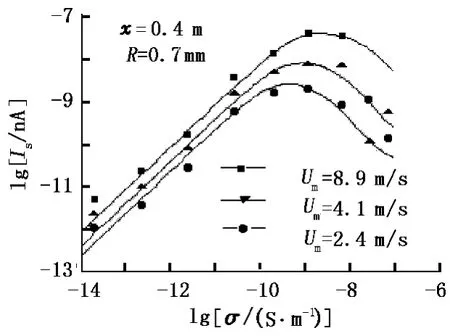
图2 冲流电流与电导率关系Fig.2 Dependence of streaming current on conductivity

Tanaka［3］在利用试验研究管壁粗糙度对流动带电的影响时，采用在管内壁上布置一些螺旋状凸块的方式模拟管壁的粗糙度，并通过调节凸块高度来调整管壁的粗糙度。计算结果和试验结果见图3和图4。

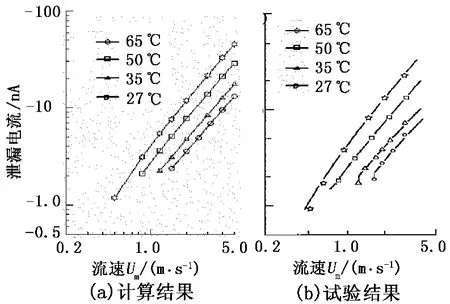
图3 不同温度下管壁没有凸块时总的泄漏电流与流速的关系Fig.3 Dependence of total leakage current on flow velocity at different temperature without protuberances

从图中可以看到，本文计算公式给出的预测值和文献［3］和［13］中的试验值非常吻合，说明该计算公式能准确预测冲流电流的大小，且推导过程中所作的简化是合理的，同时说明了该计算公式具有较广泛的适用范围。

本文给出的计算公式可用于实际管网中冲流电流的计算。其计算方法如下:将整个管网等效为网络拓扑结构相同的电路，管网中的泵、过滤器和阀门等阻力部件等效为静电荷产生源，以在该管段中增加一额外冲流电流I0来表示，然后根据基尔霍夫电流定律建立网络节点上流量、静电荷密度和冲流电流的关系矩阵，用本文的计算公式计算直管段内的冲流电流，这样就可求得管网中任意一点冲流电流的大小。

图4 不同温度下管壁有凸块时总的泄漏电流与流速的关系Fig.4 Dependence of total leakage current on flow velocity at different temperature with protuberances

4 结束语

通过对紊流态下紊流扩散系数和轴向流速的合理简化，推导出了电荷守恒方程的近似解析解，并在此基础上导出了该流态下冲流电流计算公式。同时利用相关文献的试验数据从流动带电的速度特性、温度特性和电导率特性以及管壁粗糙度对流动带电的影响等角度对冲流电流计算公式的有效性进行了验证。计算值和试验值相当吻合，说明本文给出的冲流电流计算公式具有较广泛的适用范围，而且所引入的两个修正量At和n可通过试验来确定，克服了以往公式中含有难以确定的变量的困难。

［1］ GAVIS J and KOSZMAN I.Development of charging in low conductivity liquids flowing past surfaces:a theory of the phenomenon in tubes［J］.Journal of Colloid Science，1961，16（4）:375-391.

［2］ GAVIS J.Transport of electric charge in low dielectric constant fluids［J］.Chemical Engineering Science，1964，19（3）:237-252.

［3］ TANAKA T，YAMADA N，YASOJIMA Y.Characteristics of streaming electrification in pressboard pipe and the influence of an external electric field［J］.Journal of E-lectrostatics，1985，17（3）:215-234.

［4］ ABEDIAN B，SONIN A A.Theory for electric charging in turbulent pipe flow ［J］.Journal of Fluid Mechanics，1982，120:199-217.

［5］ WALMSLEY H L，WOODFORD G.The generation of electric currents by the laminar flow of dielectric liquids［J］.Journal of Physics D:Applied Physics，1981，14（10）:1761-1782.

［6］ WALMSLEY H L.The generation of electric currents by the turbulent flow of dielectric liquids:I.long pipes［J］.Journal of Physics D:Applied Physics，1982，15（10）:1907-1934.

［7］ WALMSLEY H L.The generation of electric currents by the turbulent flow of dielectric liquids:II.pipes of finite length ［J］.Journal of Physics D:Applied Physics，1983，16（4）:553-572.

［8］ TOURCHARD G.A physicochemical explanation for flow electrification in low-conductivity liquids in contact with a corroding wall［J］.IEEE Transactions on Industry Applications，1996，32（5）:1051-1057.

［9］ TOURCHARD G.Flow electrification of liquids［J］.Journal of Electrostatics，2001，51/52:440-447.

［10］ PAILLAT T，MOREAU E，TOURCHARD G.Space charge density at the wall in the case of heptane flowing through an insulating pipe［J］.Journal of Electrostatics，2001，53（2）:171-182.

［11］ 王菊芬，蒲家宁，孟浩龙.输油管道油流带电的计算模型［J］.石油学报，2006，27（3）:133-137.

WANG Ju-fen，PU Jia-ning，MENG Hao-long.Computational model for flow electrification in oil pipeline［J］.Acta Petrolei Sinica，2006，27（3）:133-137.

［12］ TOURCHARD G，WATANABE S.Fluctuations of potential induced by turbulent flows of dielectric liquids through metallic pipes［J］.IEEE Transactions on Industry Applications，1993，29（3）:645-649.

［13］ ABEDIAN B，SONIN A A.Electric currents generated by turbulent flows of liquid hydrocarbons in smooth pipes:experiment vs theory［J］.Chemical Engineering Science，1986，41（12）:3183-3189.

Calculation of oil flow electrification current in pipeline

WANG Ju-fen，MENG Hao-long

（The Aviation Fuel and POL Equipment Test Center，Beijing100076，China）

Based on some reasonable simplification to the turbulent diffusion coefficient and axial velocity，an approximate analytical solution to the charge conservation equation and a formula of streaming current were derived.The formula which has a wide application scope，takes into account not only the influences of fluid velocity，oil conductivity and temperature on flow electrification，but also the influences of some non-quantitative factors such as wall roughness，oil aging and the electrochemical reaction at the interface between the solid wall and the liquid on flow electrification.It is proved with experimental data that the formula can correctly predict streaming current，thus providing a method to reliably and conveniently compute streaming electrification in oil pipe.

oil pipe;streaming current;charge conservation equation;analytical solution;turbulent flow

TE 832

A

10.3969/j.issn.1673-5005.2010.05.024

1673-5005（2010）05-0131-05

2009－12－30

中国人民解放军总后勤部军需物资油料部资助项目（20070402）

王菊芬（1975－），女（汉族），浙江温岭人，工程师，博士，从事油流流动带电现象研究。

（编辑 沈玉英）