基于可靠性分析与状态监测的钻井泵剩余工作寿命预测

裴峻峰，张嗣伟，齐明侠，张志毅

（1.常州大学机械与能源工程学院，江苏常州 213016;2.中国石油大学机械与储运工程学院，北京 102249;3.中国石油大学机电工程学院，山东东营 257061;4.河南石油勘探局钻井工程公司，河南南阳 473132）

基于可靠性分析与状态监测的钻井泵剩余工作寿命预测

裴峻峰1，张嗣伟2，齐明侠3，张志毅4

（1.常州大学机械与能源工程学院，江苏常州 213016;2.中国石油大学机械与储运工程学院，北京 102249;3.中国石油大学机电工程学院，山东东营 257061;4.河南石油勘探局钻井工程公司，河南南阳 473132）

在对大量同类钻井泵的大修间隔时间数据进行概率统计分析的基础上，求得与钻井泵的运行可靠度相关的特征参数，在宏观上提供钻井泵寿命预测的依据。动力端中情况最差的轴承的寿命可代表钻井泵的寿命，所以将状态监测所得的经优选的各域振动信息作为神经网络系统的模糊输入向量，通过径向基神经网络求出轴承的故障隶属度，作为轴承理论寿命计算公式的修正系数，由此解决钻井泵剩余工作寿命的预测问题，进而获得钻井泵剩余工作寿命。实际预测结果证明了预测方法的科学性和合理性。

钻井泵;动力端轴承;可靠性分析;状态监测;剩余工作寿命预测

钻井泵是石油钻井的关键设备，目前现场大多采用定期大修和事后大修，这两种大修方法虽具有可操作性，但既不经济，又给钻井生产带来隐患，因此科学确定钻井泵的大修周期（即剩余工作寿命）是保证钻井泵安全运行、节约维修费用进而保证钻井生产安全的迫切问题。钻井泵主要由动力端和液力端两大部分组成，其中液力端部件大都属于易损件，失效后可以在井场进行现场更换，而动力端中十字头和滑块之间磨损严重和轴承发生损坏，将会使泵无法工作而必须进厂大修。因为十字头的状况较易判别和处理，所以钻井泵的剩余工作寿命预测问题就转化为对钻井泵动力端轴承剩余工作寿命的预测问题。笔者采用基于Bayes方法的钻井泵可靠性分析方法，并将其与泵的状态监测与故障诊断技术融合，提出影响钻井泵动力端轴承的剩余工作寿命计算方法，求得钻井泵的剩余工作寿命预测模式及相应的预测系统。

1 钻井泵运行可靠性分析

1.1 基本方法

研究钻井泵的运行可靠性，在宏观上为确定钻井泵的大修周期提供科学依据。

钻井泵运行可靠性分析是建立在对大量钻井泵的大修间隔时间进行概率统计分析的基础上，求得与钻井泵的运行可靠性相关的特征参数，如运行周期分布概型、可靠度函数、失效概率、平均故障周期、对应运行时间的可靠度、要求可靠度下的运行寿命等。

钻井泵的运行可靠度R（t）表示泵在指定时间区间（0，t）内不发生故障的概率，R（t）的导数为随机变量的概率密度函数，记为f（t）。

由于获取的泵大修间隔时间的统计数据并不很多，因此有必要利用Bayes方法进行概率分布参数的估计，以避免由于统计数据量不足引起的统计参数的偏差，Bayes估计从定义上保证了它是在Bayes风险最小意义下的最优估计，本文中采用了推广的Bayes方法［1］。

1.2 可靠性指标确定

1.2.1 基本数据

3NB－1300C卧式三缸单作用往复泵是目前石油钻机上使用最广泛的钻井泵，通过采集江苏和河南油田多台3NB－1300C往复泵从1989至2003年的大修（运行周期（小时））数据，剔除异常数据后得到了大量的运行周期有效数据。

1.2.2 检验结果与可靠性分布

（1）K－S检验。在运行可靠性分析中，采用K－S检验法，得到如表1所示的检验结果。表1表明该泵的运行周期服从“对数正态”分布，其均值与标准差分别为¯y=9.052，σy=0.2964，此为先验分布。

（2）可靠性分布。确定出运行可靠性概率密度函数f（t）和可靠度函数R（t），并求得平均无故障间隔时间和可靠寿命tR（当泵运行可靠度为R时的对应运行时间）。

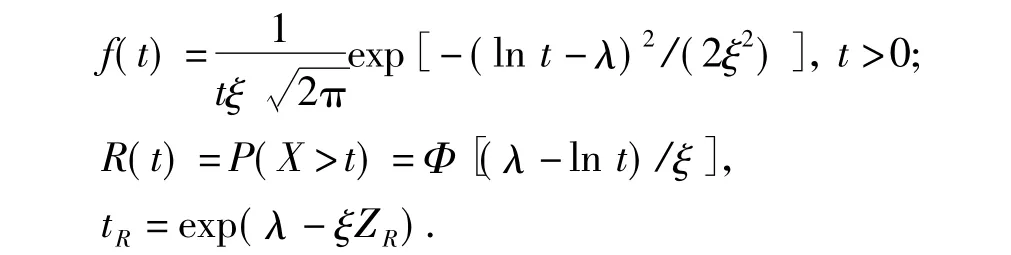
式中，λ，ξ为x（t）服从对数正态分布时的参数;ZR为概率值P=R时的标准正态分位数。

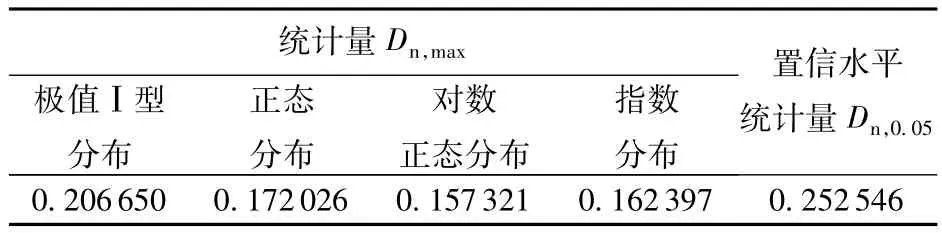
表1 K-S检验结果Table 1 K-S test result

1.2.3基于Bayes方法的钻井泵运行可靠性分布参数估计

现已知钻井泵运行周期x（t）的先验分布服从对数正态分布，令y=ln x，则y亦服从正态分布，可对变量y应用下述两式求得其后验分布参数μ″x和σ″x:

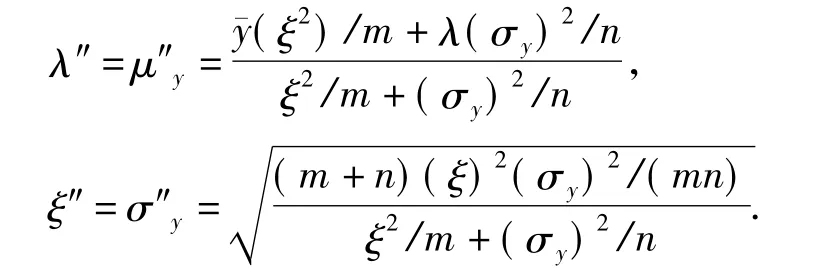
式中，m为先验分布统计中样本总数;n为x的试验样本总数。

若已知正态分布时的均值μx、标准差σx和变异系数 VX（Vx=σx/μx），则有

如x的试验值为x1，x2，…，xn，则¯y，σy分别为样本ln x1，ln x2，…，ln xn的均值和标准差。用式（1）可直接求得变量x的后验分布对数正态分布参数λ″和 ξ″。

由此推得后验概率密度函数为

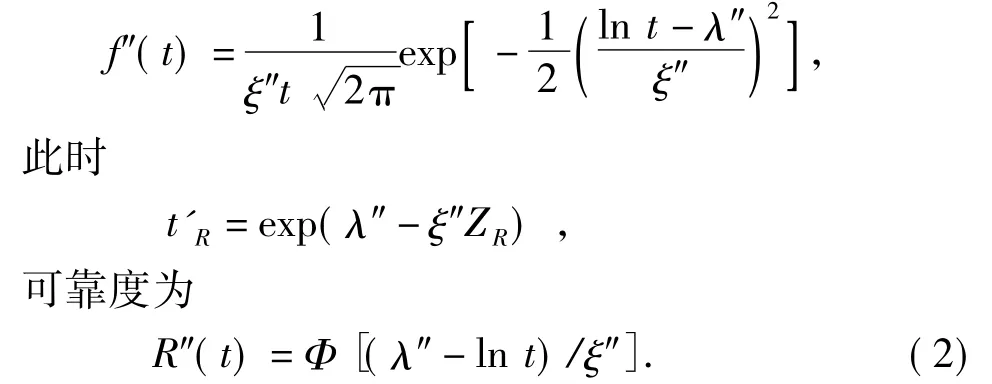
Bayes方法是对先验分布进行一个较大的修正，可减少因统计样本少所引起的偏差。

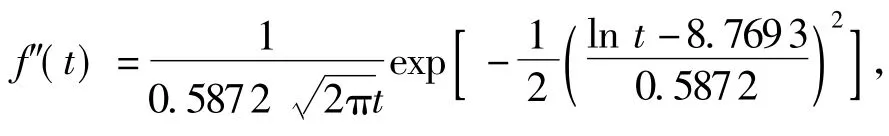
1.3 可靠性分析系统

依据可靠性分析理论和Bayes方法，编制了可用于钻井泵运行可靠性分析的软件。系统能绘制频率直方图或折线图，并显示出经过K－S检验方法检验后运行时间服从4种分布概型（极值Ⅰ型、正态、对数正态、指数）中的哪一种概型，并能绘出与运行时间对应的失效概率密度函数曲线f（t）、瞬时失效率曲线λ（t）和可靠度曲线R（t），同时给出中位运行时间t0.5和平均运行时间的数值（图1，极值Ⅰ型检验，对数正态分布检验，正态分布检验，指数分布检验的Dmax分别为0.206 649 846 355 053， 0.157 521 385 289 638，0.172026433187475，0.162397059939122，置信水平检验Dn0.05=0.252545659920791）。

求得钻井泵的可靠度函数及各项可靠性指标后，就从宏观和总体上掌握了同一类泵的运行可靠性规律，可以根据确定的可靠性指标指导状态监测周期的确定，或在规定的运行可靠度所对应的运行时间进行泵的状态监测与故障诊断。

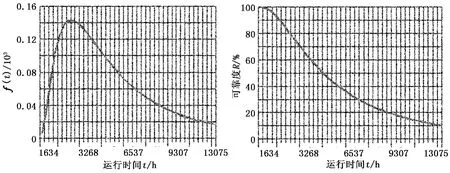
图1 3NB1300C泵运行可靠性分析系统界面Fig.1 Interface of working reliability analysis system of 3NB1300C pump

2 钻井泵剩余工作寿命预测模型

2.1 概述

运行可靠性分析可解决同一类泵的运行可靠性规律问题，但要解决具体钻井泵的剩余工作寿命预测问题，则需要建立基于状态监测的钻井泵剩余工作寿命分析预测方法和相应的系统对具体泵进行预测。将可靠性分析所得的宏观结论和状态监测系统所得的运行状态现状相结合就可较好地预测泵的运行可靠性及剩余工作寿命。目前，用于寿命预测的方法有多种，如理论模型法、进序分析法和曲线拟合法等。但这些方法一般只能对单一特征因素进行预测，而不能对复杂的运行状态及属于非线性问题的钻井泵轴承的寿命进行预测。

钻井泵轴承的寿命预测实际上是一个模糊预测问题，为了解决这个问题，可依据经验模糊量化确定工况系数指标，而其余参数指标（如幅域参数、频域参数和小波包分频带能量值等）可通过建立的基于虚拟仪器的钻井泵状态监测与故障诊断系统［6］来实测并分析得到。因此，可通过状态监测得到所需反映轴承情况的参数指标，建立一个综合考虑影响轴承寿命的指标评价体系［7］，通过建立的模糊神经网络求得轴承寿命计算公式的修正系数，进而求得钻井泵的剩余工作寿命。

2.2 预测模型

2.2.1 数学描述

轴承额定寿命的计算公式［2］为

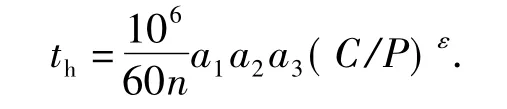
式中，th为额定寿命，h;n为轴承工作转速，r/min;a1，a2，a3分别为轴承的可靠性系数、材料系数、使用条件系数，可查有关手册确定;C为滚动轴承的额定动负荷，N;P为滚动轴承的当量动负荷，N。

轴承剩余寿命预测函数f定义为

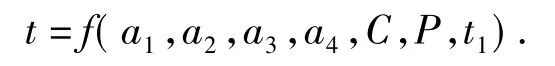
式中，t1为轴承已运转时间;a4为与轴承状态相关影响寿命的系数，a4＜1，需研究确定。因此，轴承剩余寿命可修正为

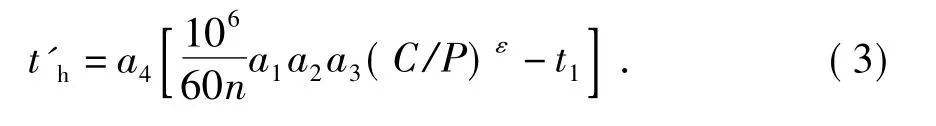
2.2.2 求解方法

泵的轴承剩余寿命预测函数f确定后，关键是要确定系数a4，剩余寿命可由下述方法确定:

（1）神经网络模型的选定。采用径向基神经网络模型进行轴承状态的识别和故障诊断。从特征参数集X中取m个数据作为网络的m个输入单元，取n个数作为网络的输出单元［8-9］。

（2）特征参数，即输入参数的确定。在幅值域参数和频域参数［3-4］中选取与运转时间关系较大的参数重心频率 FC、均方根频率 RMSF、频率标准差RVF、峭度指标 KV、峰值指标 Cf、脉冲指标 If、裕度指标CLf、歪度Sr和小波包分频带能量值［7］作为输入参数。

在神经网络训练和检测中输入和输出的目标向量实际上是一模糊值，需根据所得检测信息和经验模糊综合确定［6，10］。实际判断时，由文献［5］知:一般正常轴承的内、外圈故障模糊贴近值约在0.4以下，而0.4以上就可认为有故障而且不能再继续使用;轴承滚子故障此值约在0.2以下，而0.2以上就可认为有故障。同时，小波包分频带能量值的分布情况和运行可靠度也可作为确定输出判断量隶属度的一个重要依据:若小波包分频带能量值只在第一、二频带内出现，可认为处于正常状态;若小波包分频带能量值只在前1/3频带内出现，可认为有轻微故障;若小波包分频带能量值只在前2/3频带内出现，可认为处于报警状态;若小波包分频带能量值在全部频带（包括高频频带）内出现，可认为处于危险状态。因此，实际确定输出判断量的隶属度时，应综合考虑故障贴近值的大小和小波包分频带能量值的分布情况:两者均大者，可认为是处于危险状态，隶属度μ=0.1或接近0;两者均正常时，认为泵处在正常状态，各输出判断量的隶属度μ=1;两者有小的异常，可认为有轻微故障，输出隶属度μ=0.6;两者有中等异常，或其中之一有较大异常，认为处于报警状态，输出隶属度μ=0.4。在模糊确定时，同时考虑运行可靠度的因素，将按此方法模糊确定的与各种状态所对应的隶属度值作为神经网络训练时的输入值。

（3）故障诊断识别。将训练样本和测试样本输入神经网络进行分析计算，当达到允许误差时得到诊断结果与轴承状态相关影响寿命的系数（即网络的预测输出值）a4。

（4）剩余寿命的预测值。判别出轴承的状态后，还需求出剩余寿命的预测值，此时需考虑已运行时间、运行可靠度、十字头噪声和轴承噪声等因素，若无强烈直观异常情况，则将通过神经网络计算出的输出值a4代入轴承剩余寿命预测函数f，即可作出轴承及泵剩余工作寿命的预测。

3 应用实例

3NB－1300C钻井泵的生产商提供的曲轴轴承寿命如表2所示。轴承的th值可认为与厂方提供的设计寿命相同。需确定系数a4，进而确定泵的剩余工作寿命。

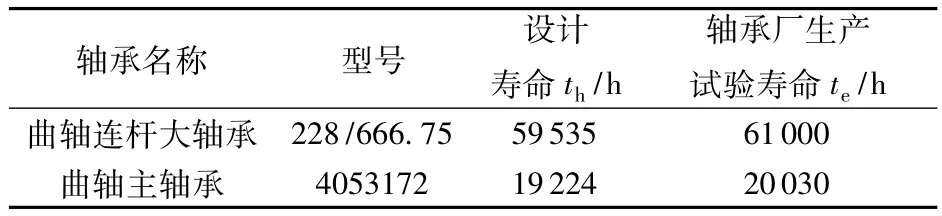
表2 3NB-1300C钻井泵曲轴轴承设计寿命Table 2 Design life of crankshaft bearing of 3NB-1300C drilling pump

随机选择河南油田0303号泵（已运行3970 h，此时可靠度为59.16%）和9503号泵（已运行13540 h，可靠度为9.88%）为研究对象。

（1）神经网络模型。选择径向基（RBF）模型。

（2）输入参数。将经过优化确定的动力端故障诊断用神经网络输入参数组合FC+RMSF+RVF+KV+Cf+If+CLf+Sr+32个小波包分频带能量值，训练用的输出判断隶属度由DPMDS系统诊断出的轴承故障的判据（外环、内环、滚子故障值）和泵的运行时间（或运行可靠度）模糊确定。

（3）确定系数a4。将选定的输入特征参数送入神经网络迭代运算，对于0303号泵，已运转3 970 h，其所有轴承中主轴承的最小的a4为0.72;对于9503号泵，已运转13540 h，其所有轴承中主轴承最小的a4为0.29。

（4）剩余工作寿命的确定。求得系数a4后，代入式（3），即可求得泵的剩余工作寿命。

0303号泵和9503号泵剩余工作寿命预测值分别为10982 ，1349 h。

此剩余寿命预测值由于综合考虑了检测所知的轴承的运行可靠性及实际状态，应用RBF网络较好地解决了系统特征参数与寿命的非线性问题，因此是合理的。实例预测表明所研究的方法是合理可行的，明显优于原来的定期维修和事后维修方法。河南油田钻井工程公司应用此预测系统在2005—2006年间先后对32615，32618等10个钻井队的18台钻井泵进行了故障诊断和寿命预测，及时找到了两台泵存在的十字导板及曲轴支撑轴承故障，作出了合理科学的大修安排，取得了良好的经济效益。

4 结束语

建立了确定钻井泵剩余工作寿命的计算模式，开发了用于钻井泵剩余工作寿命的测试及分析系统，应用RBF网络较好地解决了系统特征参数与寿命的非线性问题。由于综合考虑了轴承寿命理论、泵的运行可靠性及实际运行情况，明显要比事后维修法和定期维修法合理科学。可靠性分析与泵状态监测的融合可以提高故障诊断及剩余寿命预测的准确率;基于Bayes方法的确定钻井泵运行可靠度的方法，可为同类钻井泵的剩余工作寿命预测提供科学依据。

［1］ 张广文，刘令瑶.确定随机变量概率分布参数的推广Bayes方法［J］.岩土工程学报，1995，17（3）:91－94.

ZHANG Guang－wen，LIU Ling－yao.Extended Bayesian method of determining random variables probability distribution parameters［J］.Chinese Journal of Geotechnical Engineering，1995，17（3）:91－94.

［2］ 余俊.滚动轴承计算——额定、当量负荷及寿命［M］.北京:高等教育出版社，1993:52－54，80－83，188，217.

［3］ HOFFMAN A J，VAN der Merwe N T.The application of neural networks to vibration diagnostics for multiple fault conditions［J］.Computer Standards Interfaces，2002（24）:139－149.

［4］ SAMANTA B，AL－Balush K R.Artificial neural network based fault diagnostics of rolling element bearings using time－domain features［J］.Mechanical Systems and Signal Processing，2003，17（2）:317－328.

［5］ 裴峻峰，张嗣伟，齐明侠.共振解调和模糊识别技术在钻井泵轴承故障诊断中的应用［J］.石油学报，2005，26（4）:119－122.

PEI Jun－feng，ZHANG Si－wei，QI Ming－xia.Application of demodulated resonance and fuzzy distinguishing technique to fault diagnosis of bearings in drilling pump［J］.Acta Petrolei Sinica，2005，26（4）:119－122.

［6］ BAILLIE D C，MATHEW J A.Comparison of autoregressive modeling techniques for fault diagnosis of rolling element bearings［J］.Mechanical Signal Processing，1996，10（1）:1－17.

［7］ NIKOLAOU N G，ANTONIADIS I A.Rolling element bearing fault diagnosis using wavelet packets［J］.NDT ＆E International，2002（35）:197－205.

［8］ 飞思科技产品研发中心.神经网络理论与MATLAB7实现［M］.北京:电子工业出版社，2005:89－126.

［9］ 廖明燕.基于神经网络多参数融合的钻井过程状态监测与故障诊断［J］.中国石油大学学报:自然科学版，2007，31（4）:149－152.

LIAO Ming－yan.Drilling state monitoring and fault diagnosis based on multi－parameter fusion by neural network［J］.Journal of China University of Petroleum（Edition of Natural Science），2007，31（4）:149－152.

［10］ 许康，张劲军，陈俊，等.预测模型可靠性的模糊数学评价方法［J］.石油大学学报:自然科学版，2004，28（4）:102－104.

XU Kang，ZHANG Jin－jun，CHEN Jun，et al.A new assessment method for reliability of prediction model with fuzzy mathematics［J］.Journal of the University of Petroleum，China（Edition of Natural Science），2004，28（4）:102－104.

Drilling pump remaining working life prediction based on reliability analysis and condition monitoring

PEI Jun－feng1，ZHANG Si－wei2，QI Ming－xia3，ZHANG Zhi－yi4

（1.College of Mechanical and Energy Engineering in Changzhou University，Changzhou213016，China;2.Faculty of Mechanical and Oil-Gas Storage and Transportation Engineering in China University of Petroleum，Beijing102249，China;3.College of Electromechanical Engineering in China University of Petroleum，Dongying257061，China;4.Drilling Engineering Company，Henan Petroleum Exploration Bureau，Nanyang473132，China）

Based on probability and statistics analysis of a large number of overhaul interval time data of similar drilling pumps，the characteristic parameters related to the operating reliability of the drilling pump were obtained.These parameters provide macroscopic basis for life prediction of drilling pump.Because the life of the worst bearing at the power end represents the life of the drilling pump，each optimal domain vibration information obtained from condition monitoring was used as fuzzy input vectors of a neural network system，then the value of fault membership degree of the bearing was calculated through the RBF neural network.The value acts as the correction factor of theoretical bearing life calculation formula.As a result，the remaining working life of the drilling pump can be determined.The actual predicted results show the scientific and reasonable prediction method.

drilling pump;power end bearing;reliability analysis;condition monitoring;remaining working life prediction

TE 926;N 945.24

A

10.3969/j.issn.1673－5005.2010.05.022

1673－5005（2010）05－0121－05

2009－12－22

江苏省科技成果转化专项资金项目（BA2005041）;江苏省油气储运技术重点实验室建设项目（CY0606）

裴峻峰（1954－），男（汉族），江苏宜兴人，教授，博士，主要从事石油及石化设备的可靠性及故障诊断的教学和研究工作。

（编辑 沈玉英）