一种新的流变模式及其应用性评价

樊洪海，冯广庆，王果，2，刘阳，张辉

（1.中国石油大学石油工程教育部重点实验室，北京 102249;2.中国石化石油工程技术研究院钻井工艺研究所，北京 100101; 3.斯坦福大学，美国加利福尼亚州斯坦福市 94305;4.胜利油田钻井工程技术研究院，山东东营 257017）

一种新的流变模式及其应用性评价

樊洪海1，冯广庆1，王果1，2，刘阳3，张辉4

（1.中国石油大学石油工程教育部重点实验室，北京 102249;2.中国石化石油工程技术研究院钻井工艺研究所，北京 100101; 3.斯坦福大学，美国加利福尼亚州斯坦福市 94305;4.胜利油田钻井工程技术研究院，山东东营 257017）

在评价现有流变模式的适应性和优缺点的基础上，提出一种新的4参数流变模式，利用回归分析的数学方法对各流变模式的流变参数进行数据处理，并对各流变模式的参数确立和评价进行研究，应用不同类型的钻井液测量数据对各流变模式进行回归计算与分析。结果表明:在试验用的6种钻井液中，4参数流变模式能较好地反映各剪切速率下的钻井液流变性，最为精确，拟合效果最好，适用于各种钻井流体;拟合效果由好到差依次为4参数、赫巴、卡森、幂律、宾汉模式。

流变学;流变模式;流变参数;4参数模式;应用评价;回归分析

非牛顿流体流变特性及流动规律的研究是石油工业中经常遇到的问题。本构方程的建立和流变参数的确定，是研究非牛顿流体流动和流变特性的基础，对优化钻井、水力计算、参数优选分析具有十分重要的作用。水平井、深井和小井眼水力学对钻井水力参数的计算提出了更苛刻的要求。因此，如何准确表达钻井液在钻柱和环空中的流变特性显得尤为重要。目前在石油工业中常用的流变模式有宾汉、幂律、卡森、赫谢尔-巴尔克莱模式等［1-10］。这些流变模式只能近似地表示钻井液的实际流变特性，无法在全剪切率范围内准确地描述各种钻井流体的流变特性。现有的这些流变模式因其自身的适应性和优缺点，较难得到精确而实用的计算。笔者提出一种新的4参数流变模式，并对其进行现场适用性评价。

1 现有流变模式及其评价

1.1 流变模式评价方法

按照流体流动时剪切速率和剪切应力之间的关系，流体可以划分为不同的流变模式。一般来说，按流变模式可把流体划分为牛顿流体、塑性流体、假塑性流体和膨胀性流体。许多研究者作了大量的科学试验，根据不同的流变曲线给出了相应的数学关系式，提出了相应的流变模式。一种完善的流变模式应具备的条件是:

（1）不同速度梯度范围内剪切应力的实测值与理论值较为符合。

（2）根据不同的流道（管内、环空）可以推导出既精确又简单的流变参数计算式。

（3）使用范围广，能很好地适用于各种类型的钻井液。

1.2 现有流变模式及其评价

式中，τ为剪切应力，Pa;τ0为屈服应力，Pa;η为宾汉塑性黏度，Pa·s;γ为剪切速率，s－1;τc为卡森屈服应力，Pa;η∞为卡森塑性黏度，Pa·s;K为幂律或赫－巴模式稠度系数，Pa·sn;n 为幂律或赫巴模式流性指数;A为R-S模式稠度系数，Pa·sB;B为R-S模式流性指数;C为R-S模式剪切稀释系数，s－1;a为双曲、Sisko模式稠度系数，Pa·s;b为双曲模式剪切稀释系数，s－1（或Sisko模式稠度系数，Pa ·sc）;c为Sisko模式流性指数。

很多学者对这些流变模式的水力计算与应用进行了评价与优选［20-26］。评价结果如下:

（1）宾汉模式和幂律模式在一定程度上能反映各自流体在中、高剪切速率下的流动规律，但不能反映低剪切速率下流体的流动规律，而携带岩屑液流的剪切速率往往不会很高，并且幂律模式不能反映钻井液具有屈服应力的特性。

（2）卡森模式一般优于塑性流体和假塑性流体，但其流变参数的意义不够明显。赫巴模式在特定条件下能够反映牛顿流体、塑性流体和假塑性流体的特性，但不能反映卡森流体的流变特性。

（3）

双曲模式与赫巴和R-S模式一样，当剪切速率γ趋近于∞时，视黏度μ=τ/γ趋向于0，说明不存在极限黏度，不符合多数钻井液实际情况。

（4）Sisko模式能反映多数钻井液的剪切稀释性，存在极限黏度，符合多数钻井液实际情况，但是没有反映钻井液具有屈服应力的特性。这样，Sisko模式在中、高剪切速率式更好地提高了拟合精度，但在低剪切速率区仍显不足。

2 4参数流变模式

现有流变模式都存在一定的局限性，无法在全剪切速率范围内准确地描述各种钻井流体的流变特性。因此，在研究现有流变模式的基础上，笔者提出一种新的能适用多种钻井流体、在全剪切速率范围内准确描述其流变性的4参数模式。

2.1 4参数流变方程

Sisko模式是一种较先进的3参数模式，但它没考虑流体的屈服值，这点在低剪切速率时有尤为明显的缺陷。考虑到多数钻井液带有屈服值的特点，在Sisko模式基础上提出一种4参数流变模式，即

式中，a1为牛顿流体部分的黏度，即剪切速率无限大时的黏度，Pa·s;b1为非牛顿流体部分的黏度（剪切速率越小这一项所起的作用越大），Pa·sc;c1为流性指数，c1＜1为假塑性流体，c1＞1为膨胀性流体。

当剪切速率γ趋近于0时，剪切力τ也趋近于τ0，这反映大多数钻井液所具有的屈服应力的特点，弥补了幂律和Sisko模式的不足。相对于赫巴模式，它又增加了对流变曲线形状控制的参数，视黏度为μ=τ/γ=τ0γ－1+a1+b1γc1－1。多数钻井液为假塑性流体（c1＜1），当剪切速率γ增加时，μ随之减小，能反映多数钻井液剪切稀释的特点，而且该模式保留了Sisko模式的优点，当剪切速率γ趋近于∞时，μ趋向于极限黏度a1，符合多数钻井液实际情况。

2.2 流变参数求解

计算钻井液的流变参数有两种方法［24-26］。

（1）直接法。该方法用传统的公式推导，不经过条件设定和假设简化，结合一些实际的测量数据（主要是旋转黏度计的），确定流变模式的参数。该方法无限定和简化，结果直接可靠，但仅能用于宾汉、幂律和卡森等线性或特殊的非线性公式，一般常用来为回归计算提供初值。

（2）回归法。在科学的统计方法研究中，往往要从一组试验数据（xi，yi）（i=0，1，…，m）中寻找自变量x与因变量y之间的函数关系式y=F（x）。由于观测数据不准确，因此不要求y=F（x）经过所有点（xi，yi），而只要求在给定点xi上误差δi=F （xi）－yi（i=0，1，…，m）按某个标准最小。首先要确定y=F（x）的形式。这不单纯是数学问题，还与所研究问题的运动规律及所得观测数据（xi，yi）有关，通常要从问题的运动规律及给定数据描绘确定y=F（x）的形式，并通过实际计算选出较好的结果。

变量x与y的线性相关程度由相关系数R来衡量，即

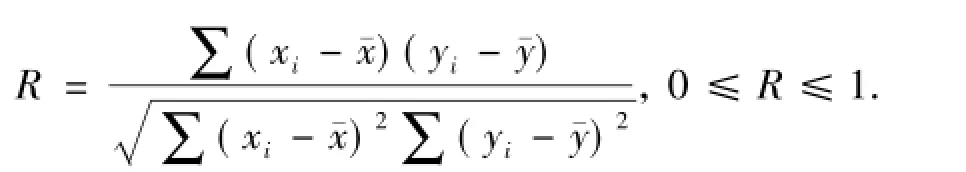
R越接近0，x与y之间的相关程度越小，线性回归效果越差;R越接近1，x与y之间的相关性越密切，回归效果越好。因此，可以根据相关系数R判定哪种流变模式最符合试验数据。相关系数的取值至关重要，因为它是对于各流变模式计算误差的一个综合度量值，并且可以精确描述各流变模式变量间的紧密结合程度。

3 实例验证

用回归方法得到各模式的流变参数，然后用相关系数R表征它们各自的拟合效果。分别选取了典型的宾汉、幂律、卡森、赫巴和4参数模式进行比较。采取的现场试验数据为文献［22］中的钻井液测量数据，选用的钻井液体系有水基钻井液（1）、油基钻井液（2）、加重钻井液（3）、新型MMH钻井液（4）及低屈服值（5）和高屈服值钻井液（6），如表1所示。

根据表1的测量数据，对各流变模式的流变参数进行回归，结果见表2。根据表2回归结果绘制各流变模式的流变曲线并与实测值进行对比（图1，对每种钻井液只给出了与实测值最接近的3种流变模式的流变曲线）。图2为各流变模式总体回归效果的比较（图2中对每种钻井液从左到右依次为宾汉、幂律、卡森、赫巴、4参数模式的相关系数）。

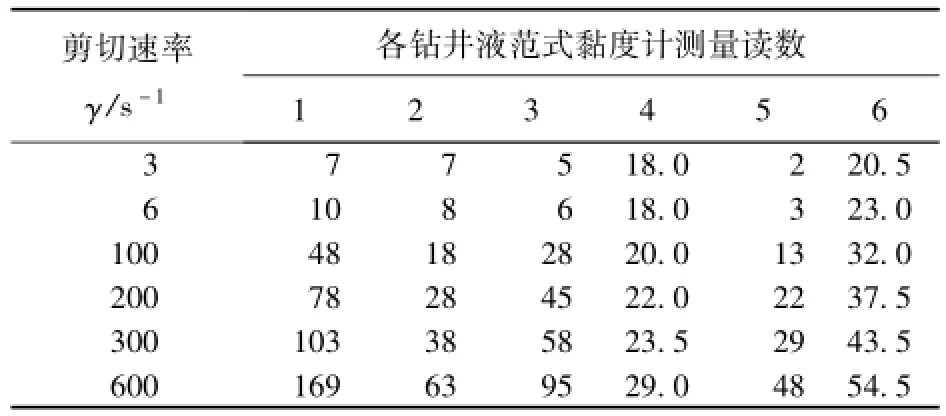
表1 各钻井液原始数据Table 1 Initial data of drilling fluids

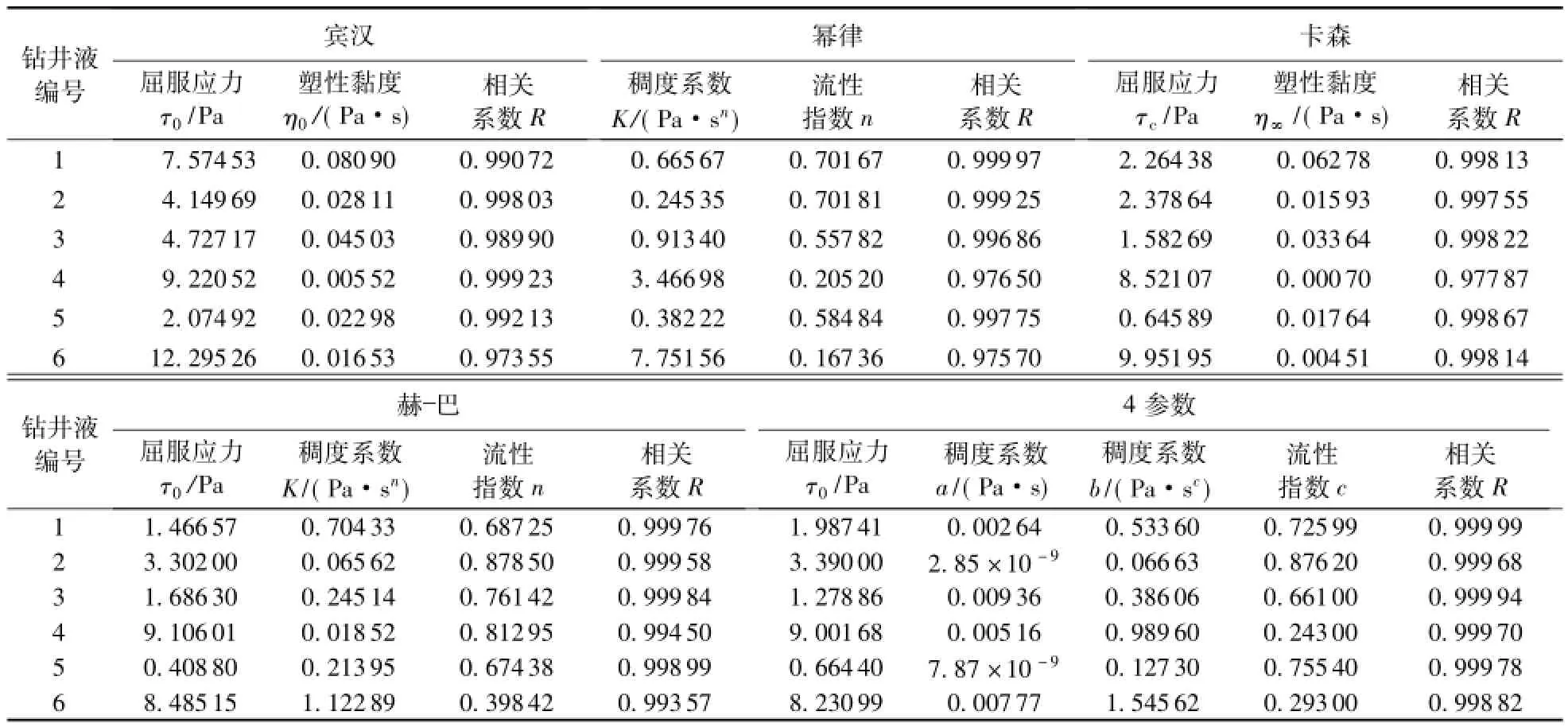
表2 不同配方钻井液计算结果Table 2 Calculated resu lts of drilling fluidswith different formu la

图1和表2的结果表明:对于各种类型的钻井液，4参数流变模式在各剪切速率下都与实测值最为吻合，能准确表达其流变性能;幂律模式比较适于表达水基钻井液的性能（图1（a）），而对于有一定屈服值的钻井液，在低剪切速率下就不能很好地描述其流变性（图1（b））;宾汉模式比较适合表达新型MMH钻井液，因为其流变曲线具有高屈服应力和近似直线的特点，故宾汉模式的拟合效果几乎与4参数模式的一样好（图1（d））;卡森模式的主要特点在于它能够近似地描述钻井液在高剪切速率下的流动性，比较适合表达具有高屈服应力钻井液的性能（图1（f）），但是因为其曲线在中高剪切速率下比较平直，不能很好地表达钻井液的特性（图1（c）和图1（e））;赫巴模式是除了4参数模式外适应性比较好的一种流变模式，但其不能很好地表达钻井液在高剪切速率下的性能，对某些钻井液在高剪切速率下的拟合偏差很大（图1（d），（e），（f））。

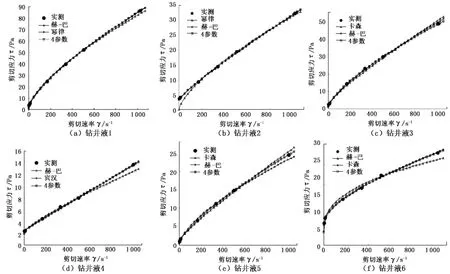
图1 流变模式拟合值与实测值对比Fig.1 Com parison of rheological parameters fitting results and testing results

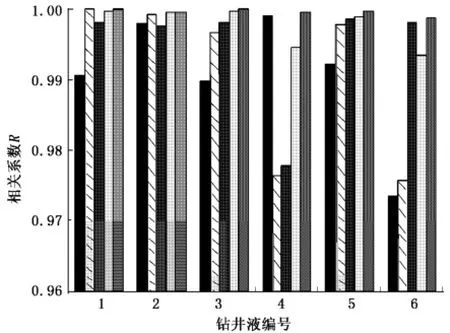
图2 不同钻井液体系下各流变模式回归结果Fig.2 Rheologicalmodels'regression results of typical drilling fluids

由图2可见，4参数流变模式拟合效果最好，然后依次是赫巴模式、卡森模式、幂律模式、宾汉模式。宾汉、幂律、卡森模式在不同钻井液体系下的回归效果变化较大，只适用于特定类型的钻井液;赫巴模式的回归效果较好，能较好地表达各种类型的钻井液，具有一定的适应性。因此，在全剪切速率范围内描述钻井液流变性时，4参数模式比其他流变模式相关性都有很大提高，且最为精确。

4 结束语

分析总结了现有流变模式的适应性和优缺点，提出了一种新的描述钻井液流变性能的4参数流变模式。利用回归分析的数学方法，建立了各流变模式的回归分析模型。本文中提出的4参数流变模式比其他流变模式相关系数都有提高，最为精确，能很好地描述钻井液在不同剪切速率下的流变性能，适用于各种钻井液流体。

［1］BINGHAM E C.Fluidity and Plasticity［M］.New York: McGraw-Hill Book Co，1922.

［2］OSTWALD W.The velocity function of viscosity of disperse systems［J］.Kolloid-Zeit，1925，36:99-117.

［3］WAELE A D.Viscometry and plastometry［J］.Oil＆Colour Chemists Assoc，1923，6（38）:33-88.

［4］FARROW F D，LOWE G M.The flow of strarch paste through capillary tubes［J］.Textile Inst，1923，14:414-440.

［5］CASSON N.A flow equation for pigment-oil suspensions of the printing ink type［D］.Swansea:British Society of Rheology，University College，Swansea，UK，1957.

［6］陈家琅，刘崇建.卡森液体的结构流和流变参数测定［J］.石油学报，1982，3（2）:69-80.

CHEN Jia-lang，LIU Chong-jian.Structural flow of Casson fluids and determination of Casson rheological parameters［J］.Acta Petrolei Sinica，1982，3（2）:69-80.

［7］HERSCHELW H，BULKLEY R.Measurement of consistency as applied to rubber-benzene solutions:Proc 29thAnnual Meeting of the American Soc Testing Materials，Atlantic City［C］.Atlantic，1926:621-629.

［8］ZAMORA M，LORD D L.Practical analysis of drilling mud flow in pipes and annuli［R］.SPE 4976，1974.

［9］REED TD，PILEHVARIA A.A new model for laminar，transitional and turbulent flow of drillingmuds［R］.SPE 25456，1993.

［10］西南石油学院固井科研组.适合钻井液及水泥浆的赫谢尔-巴尔克莱流变模式及其应用［J］.西南石油学院学报，1983，5（4）:1-15.

Cementing Research Group.Herschel-Bulkley rheologicalmodel of drillng fluid and cement slurry and its application［J］.Journal of Southwest Petroleum Institute，1983，5（4）:1-15.

［11］OKAFOR M N，EVERS JF.Experimental comparison of rheologymodels for drilling fluids［R］.SPE 24086，1992.

［12］刘崇建.带屈服值的幂律流变模式在钻井泥浆中的应用［J］.天然气工业，1982，2（3）:46-55.

LIU Chong-jian.Application ofyield power-lawmodel in drillingmuds［J］.Natural Gas Industry，1982，2（3）: 46-55.

［13］ROBERTSION R E，Jr STIFFH A.An improved mathematicalmodel for relating shear stress to shear rate in drilling fluids and cement slurries［R］.SPE 5333，1976.

［14］黄逸仁.适用于钻井液的罗伯逊-斯蒂夫模式［J］.西南石油学院学报，1982，4（2）:16-28.

HUANG Yi-ren.Robertson-stiff model applicable for drilling fluid［J］.Journal of Southwest Petroleum Institute，1982，4（2）:16-28.

［15］白家祉.带屈服值的假塑性流体的双曲模式方程与压降计算式［J］.石油学报，1980，1（2）:57-62.

BAI Jia-zhi.A new hyperbolic model of yield-pseudoplastic fluids and pressure drop formulas［J］.Acta Petrolei Sinica，1980，1（2）:57-62.

［16］白家祉，姚荣魁.“带屈服值的假塑性流体的双曲模式方程与压降计算式”一文的试验验证［J］.石油学报，1980，1（3）:49-57.

BAIJia-zhi，YAO Rong-kui.Experimental verifications on"a new hyperbolic model equation for yield-pseudoplastic fluids and related pressure drop formulas"［J］.Acta Petrolei Sinica，1980，1（3）:49-57.

［17］SISKO AW.The flow of lubricating greases［J］.Industrial＆Engineering Chem istry，1985，50（12）:1789-1792.

［18］BAILEY W J，PENDEN JM.A generalized and consistent pressure drop and flow regime transition model for drilling hydraulics suitable for slimhole，underbalanced and horizontal wells［R］.SPE/IADC 39281，1997.

［19］BAILEY W J，PENDEN JM.A generalized and consistent pressure drop and flow regime transistion mode for drilling hydraulics［R］.SPE 62167，2000.

［20］WEIR LS，BAILEYW J.A statistical study of rheologicalmodels for drilling fluids［R］.SPE 36359，1996.

［21］泥浆流变学研究组.适用于钻井液的流变模式的初步评价［J］.西南石油学院学报，1983，5（4）:17-37.

Mud-Rheology Research Group.Evaluation of the rheologicmodels of drilling fluids［J］.Journal of Southwest Petroleum Institute，1983，5（4）:17-37.

［22］汪海阁，刘希圣.钻井液流变模式比较与优选［J］.钻采工艺，1996，19（1）:63-67.

WANG Hai-ge，LIU Xi-sheng.Comparison and optimization of drilling fluid rheologicalmodels［J］.Drilling＆Production Technology，1996，19（1）:63-67.

［23］郭小阳，刘崇建，马思平.非牛顿液体流变模式的研究［J］.天然气工业，1997，17（4）:43-49.

GUO Xiao-yang，LIU Chong-jian，MA Si-ping.Research on non newtonian liquid rheological mode［J］.Natural Gas Industry，1997，17（4）:43-49.

［24］胡茂焱，尹文斌，郑秀华，等.钻井液流变参数计算软件的开发及流变模式的优化［J］.钻井液与完井液，2005，22（1）:28-30.

HU Mao-yan，YINWen-bin，ZHENG Xiu-hua，etal.A drilling fluid rheological parameter calculation software and the rheological model's optimization［J］.Drilling Fluid and Completion Fluid，2005，22（1）:28-30.

［25］周长虹，崔茂荣，黄雪静.钻井液常用流变模式及其优选方法［J］.中国科技信息，2005，22:86-87.

ZHOU Chang-hong，CUIMao-rong，HUANG Xue-jing. Conventional rheological models and optimization methods of drilling fluids［J］.China Science and Technology Information，2005，22:86-87.

［26］张辉，樊洪海，逄淑君.钻井液流变参数计算方法及现场应用软件开发［J］.西部探矿工程，2008，20 （2）:72-73.

ZHANG Hui，FAN Hong-hai，PANG Shu-jun.Calculation methods of rheological parameters of drilling fluid and on-site calculation software development［J］.West-China Exp loration Engineering，2008，20（2）:72-73.

A new rheologicalmodel and its app lication evaluation

FAN Hong-hai1，FENG Guang-qing1，WANG Guo1，2，LIU Yang3，ZHANG Hui4
（1.MOE Key Laboratory of Petroleum Engineering in China University of Petroleum，Beijing 102249，China; 2.SINOPEC Research Institute of Petroleum Engineering，Beijing 100101，China; 3.Stanford University，Stanford，California 94305，USA; 4.Drilling Technology Research Institute，ShengliOilfield，Dongying 257017，China）

A new four-parameter drilling fluid rheologicalmodel was proposed based on the evaluation of adaptation and virtues and defects of available rheologicalmodels.The parameters of rheologicalmodelswere treated by using regression analysismethod，and the rheological parameterswere determined and evaluated.The rheologicalmodels were regressed and analyzed by testing data of different types of drilling fluid.The results show that for the testing six kinds of drilling fluids，the four-parametermodel could accuratly express drilling fluid rheological characteristics under different shear rates，and achieve the bestmatching effect and apply to all kinds of drilling fluids.The order ofmatching effect from good to poor is four-parameter，H-B，Casson，power-law and Bingham model.

rheology;rheologicalmodel;reheological parameter;four-parametermodel;application evaluation;regression analysis

TE 254

A

10.3969/j.issn.1673-5005.2010.05.016

1673-5005（2010）05-0089-05

2009－12－14

国家科技重大专项课题（2008ZX05021－003）

樊洪海（1962－），男（汉族），山东章丘人，教授，博士，博士生导师，主要从事地层压力确定技术、油气井信息工程、油气井流体力学与钻井液流变学的研究。

（编辑 李志芬）