生长褶皱发育模式

郭卫星,漆家福,李明刚,李艳友

(1.中国石油大学资源与信息学院,北京 102249;2.中国石油大学油气资源与探测国家重点实验室,北京 102249)

生长褶皱发育模式

郭卫星1,2,漆家福1,2,李明刚1,李艳友1

(1.中国石油大学资源与信息学院,北京 102249;2.中国石油大学油气资源与探测国家重点实验室,北京 102249)

根据褶皱形成的运动学特征,对膝折带迁移、翼部旋转和混合生长 3种模式的沉积与抬升关系进行探讨,并针对 3种褶皱发育模式提出利用生长地层厚度推测褶皱抬升速率与褶皱过程的方法。研究表明:以膝折带迁移为变形机制的褶皱,发育过程中翼部倾角不变,褶皱顶部与翼部的抬升速率相同,形成翼部平行状生长地层;以翼部旋转为变形机制的褶皱,发育过程中翼部长度不变,沿翼部各点的抬升速率呈线性变化,形成翼部楔状的生长地层;以混合生长为变形机制的褶皱,发育过程中翼长和翼部倾角都发生变化,部分生长地层呈平行状,反映了膝折带迁移的特征,部分生长地层呈楔状,各点的抬升速率仍呈线性变化,反映了翼部旋转的特征。

构造抬升速率;沉积速率;膝折带迁移模式;翼部旋转模式;混合生长模式

生长地层常常与生长断层、生长褶皱相伴生,并详细记录了断层、褶皱的构造演化过程。利用生长地层研究断层的活动性已经得到广泛应用[1]。生长地层的厚度、岩相和形态为研究生长断层活动速率、活动时期及活动过程提供了重要信息[2]。利用生长地层的形态分析褶皱运动学特征以及断层与褶皱相互关系,近年来引起了构造地质学家的重视[3-7]。Suppe等[4]提出了生长断层转折褶皱和生长地层、生长三角的概念,Poblet等[5-6]建立了生长断层传播褶皱和生长断层滑脱褶皱的几何学和运动学模型。目前对生长褶皱的研究主要是利用生长地层判断构造起始时间和确定生长三角的生长速率[4,8-12],但这具有一定的局限性,对不发育生长三角、生长三角不明显的地层难以应用。笔者提出利用生长地层厚度推测褶皱抬升速率与褶皱过程的方法,用来指导褶皱变形运动学特征和褶皱活动期次的研究。

1 生长地层厚度分析

厚度分析的理论基础是沉积补偿原理[13]。生长褶皱 (断层转折褶皱、断层传播褶皱和滑脱褶皱)的发育有多种几何学、运动学模型 (图 1,2),但按其形成的运动学特征可分为膝折带迁移、翼部旋转和混合生长 (膝折带迁移、翼部旋转共同作用)3种模式[14]。本文中对这 3种模式的沉积速率与构造抬升速率关系逐一进行分析。

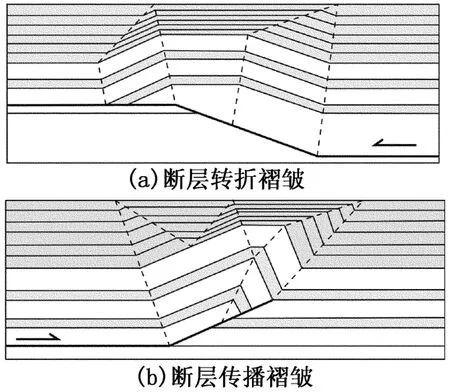
图 1 断层转折褶皱、断层传播褶皱及其生长地层 (据文献[4]修改)Fig.1 Growth fault-bend fold and growth faultpropagation fold(modified according to literature[4])

图 2 滑脱褶皱形成的不同生长地层 (据文献[5,6]修改)Fig.2 Growth strata patterns formed by detachment folds(modified according to literature[5,6])

1.1 膝折带迁移模式

膝折带迁移模式中,褶皱的发育通过轴面迁移、翼部增长来实现。发育过程中翼部倾角不变,所以褶皱顶部与翼部的抬升速率相同。褶皱顶部的生长地层通过活动轴面进入翼部而引起翼长变化、褶皱的抬升 (图 1(a)、图 3)。由于褶皱顶部的生长地层等厚,在褶皱翼部形成平行状的生长地层,即所谓的“生长三角”。

1.1.1 超 覆

沉积速率大于褶皱抬升速率时,新的生长地层叠加覆盖在老的生长地层之上 (图 3(a))。地层Ⅱ沉积前,地层Ⅰ顶面水平,地层Ⅰ位于活动轴面以上的部分,在地层Ⅱ沉积期间与褶皱一起抬升,其抬升量与褶皱相同,褶皱顶部形成薄的沉积地层,同时部分地层Ⅰ通过活动轴面进入褶皱翼部,随着进入褶皱翼部时间从早到晚,其抬升量从大变小,其上地层Ⅱ的厚度从小变大,直至盆地内形成厚的沉积地层。若地层Ⅱ在盆地内的沉积厚度为 S0、在褶皱顶部的厚度为 S1,地层Ⅱ沉积过程中褶皱抬升量为 U,则 U=S0-S1;若地层Ⅱ的沉积时间为 t,地层Ⅱ沉积期间褶皱的抬升速率为 v,则 v=(S0-S1)/t。

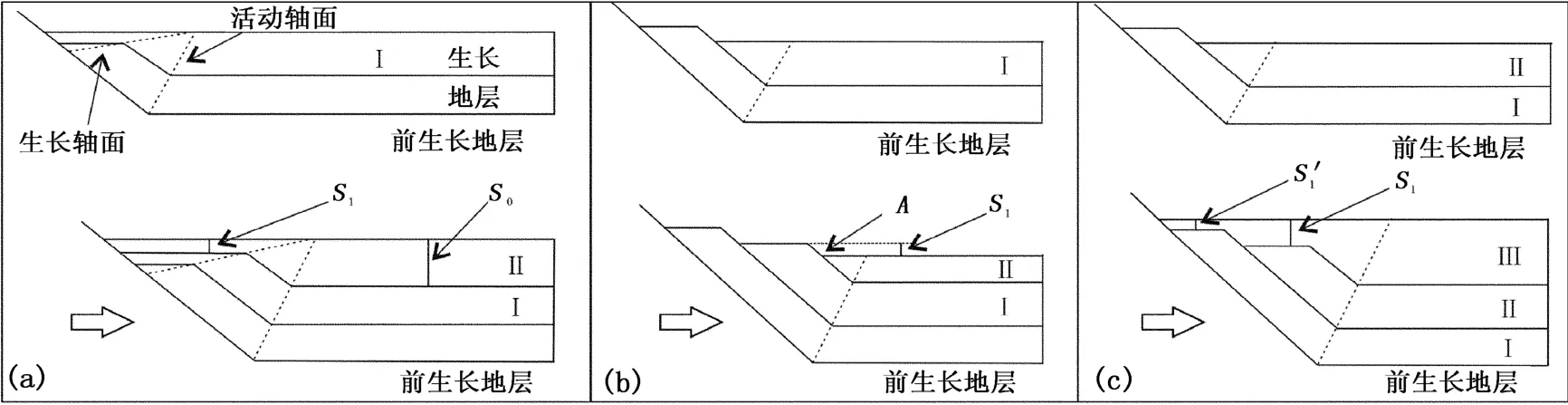
图 3 生长褶皱膝折带迁移模式中生长地层的形态Fig.3 Growth strata patterns formed by hinge m igration of growth fold

1.1.2 退 覆

沉积速率小于褶皱抬升速率时,新的生长地层逐渐向盆地方向后退 (图 3(b))。在地层Ⅱ沉积前,地层Ⅰ位于活动轴面以上的部分在地层Ⅱ沉积期间与褶皱一起抬升,抬升量与褶皱相同,其上无沉积,同时部分地层Ⅰ通过活动轴面进入褶皱翼部,这部分地层的抬升量小于褶皱的抬升量,其中地层Ⅰ顶面上一 A点的抬升量与地层Ⅱ在盆地内的沉积厚度相同,成为地层Ⅱ的尖灭点。若地层Ⅱ在盆地内的沉积厚度为 S0,地层Ⅱ顶面到褶皱翼部地层Ⅰ顶面的距离为 S1,地层Ⅱ沉积期间褶皱抬升量为U,则有 U=S0+S1。

1.1.3 上 超

退覆之后的上超,沉积速率大于褶皱抬升速率(图 3(c))。在地层Ⅲ沉积前,地层Ⅱ位于活动轴面以上的部分,在地层Ⅲ沉积期间与褶皱一起抬升,其抬升量与褶皱相同,故有 U=S0-S1,其中 S1为褶皱翼部地层Ⅱ顶面到地层Ⅲ顶面的距离。需要注意的是,由于之前的退覆作用,褶皱翼部地层Ⅱ、地层Ⅰ顶面间已经有古地形高差存在,不可将褶皱翼部地层Ⅰ顶面到地层Ⅲ顶面的距离 S′1作为 S1。

膝折带迁移主要形成断层转折褶皱 (图 1(a))、断层传播褶皱 (图 1(b))和滑脱褶皱 (图 2(a))。图3中活动轴面位于褶皱向斜处,生长地层从盆地内经活动轴面进入褶皱翼部,这种情况对应于断层转折褶皱的后翼、断层传播褶皱的前翼及滑脱褶皱的两翼;活动轴面也可位于褶皱的背斜处,生长地层从褶皱顶部经活动轴面进入褶皱翼部,如断层转折褶皱的前翼;生长地层也可同时位于褶皱一翼的背斜、向斜处,生长地层分别从盆地、褶皱顶部进入翼部,形成两个生长三角,如断层传播褶皱的后翼。

1.2 翼部旋转模式

翼部旋转模式中褶皱的发育是随着翼部旋转倾角逐渐增大来实现的,发育过程中翼部长度不变。褶皱顶部的高度 (h)可以用翼长 (L)和翼倾角 (θ)表示,即 h=Lsinθ。若褶皱过程中翼倾角由θ1变为θ2,则 U=L(sinθ2-sinθ1),可以看出翼部各点的抬升量与长度呈线性关系,导致翼部的生长地层厚度也呈线性变化,形成翼部楔状的生长地层。

1.2.1 超 覆

如图 4(a)所示,当沉积速率大于褶皱抬升速率时,褶皱顶部形成薄的沉积层,翼部各点的抬升速率呈线性变化,形成翼部楔状的生长地层。与膝折带迁移模式中的超覆相同,若地层Ⅱ在盆地内的沉积厚度为 S0、在褶皱顶部的厚度为 S1,地层Ⅱ沉积过程中褶皱抬升量为 U,则 U=S0-S1。

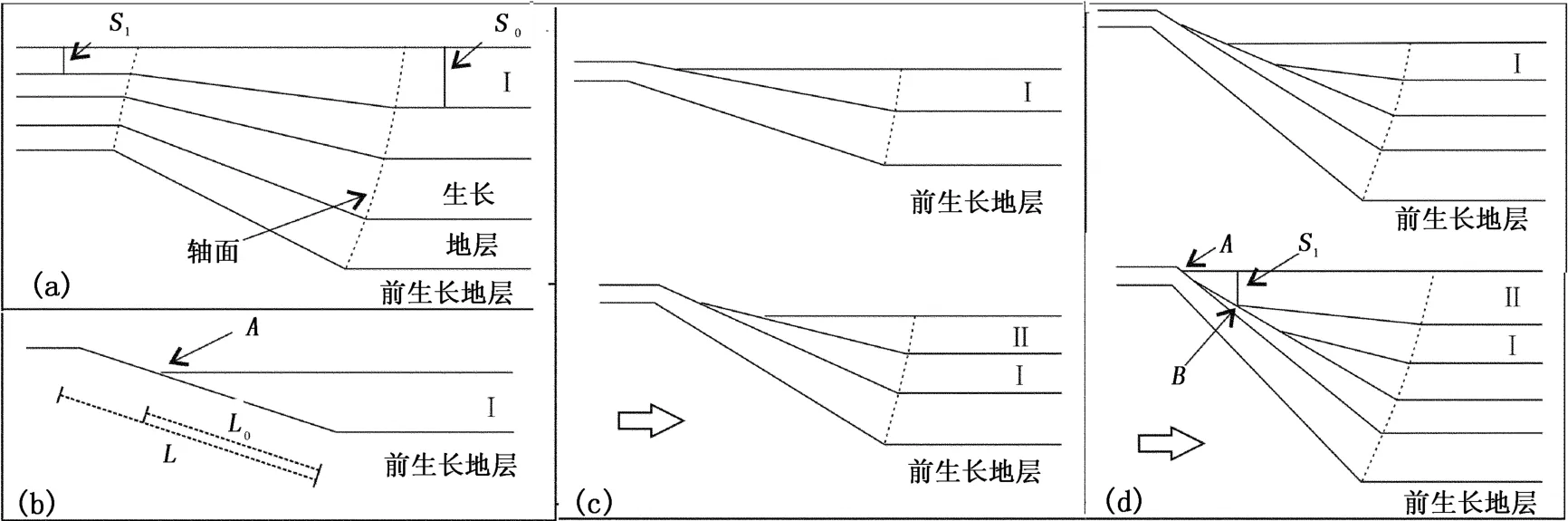
图 4 生长褶皱翼部旋转模式中生长地层的形态Fig.4 Growth strata patterns formed by l imb rotation of growth fold

1.2.2 退 覆

下伏为前生长地层的退覆如图 4(b)所示。在地层Ⅰ沉积期间,翼部逐渐旋转抬升,其上一点 A的抬升速率与沉积速率相同,成为地层Ⅰ的尖灭点,故A点抬升量等于盆地内地层Ⅰ的沉积厚度 S0。由于翼部各点的抬升量呈线性变化,可知地层Ⅰ沉积期间褶皱顶部的抬升量 U=S0L/L0。对于图 4(c),下伏为生长地层的退覆,也可用相似的方法求出褶皱顶部的抬升量及抬升速率。

1.2.3 上 超

退覆之后的上超如图 4(d)所示。在地层Ⅱ沉积期间,地层Ⅰ位于轴面以上的部分逐渐旋转抬升,造成地层Ⅱ位于轴面之上的地层部分呈楔状。若地层Ⅱ在盆地内的沉积厚度为 S0、在地层Ⅰ的尖灭点B之上的厚度为 S1,地层Ⅱ沉积期间 B点的抬升量为UB,则 UB=S0-S1,由此可以计算出褶皱的抬升量及抬升速率。需要注意的是,由于之前的退覆作用,点 A,B之间已经有古地形高差存在,故地层Ⅱ的尖灭点 A并不代表其抬升速率等于地层Ⅱ的沉积速率。

翼部旋转形成滑脱褶皱 (图 2(b)),另外三角剪切机制形成的断层传播褶皱前翼也具有翼部旋转的特征。需要指出的是在翼部旋转的同时,轴面产生有限的活动,会有少量的地层通过轴面进入翼部,形成小的生长三角[15](图 2(b))。

1.3 混合生长模式

混合生长模式(膝折带迁移和翼部旋转共同作用)中,褶皱的发育是随着翼部旋转倾角逐渐增大,并伴有轴面迁移翼部增长。从图 5可以看出,地层通过下方的活动轴面进入褶皱翼部,在翼部较低部位形成平行状的生长地层,反映了膝折带迁移的特征,在翼部较高部位形成楔状的生长地层,反映了翼部旋转的特征。

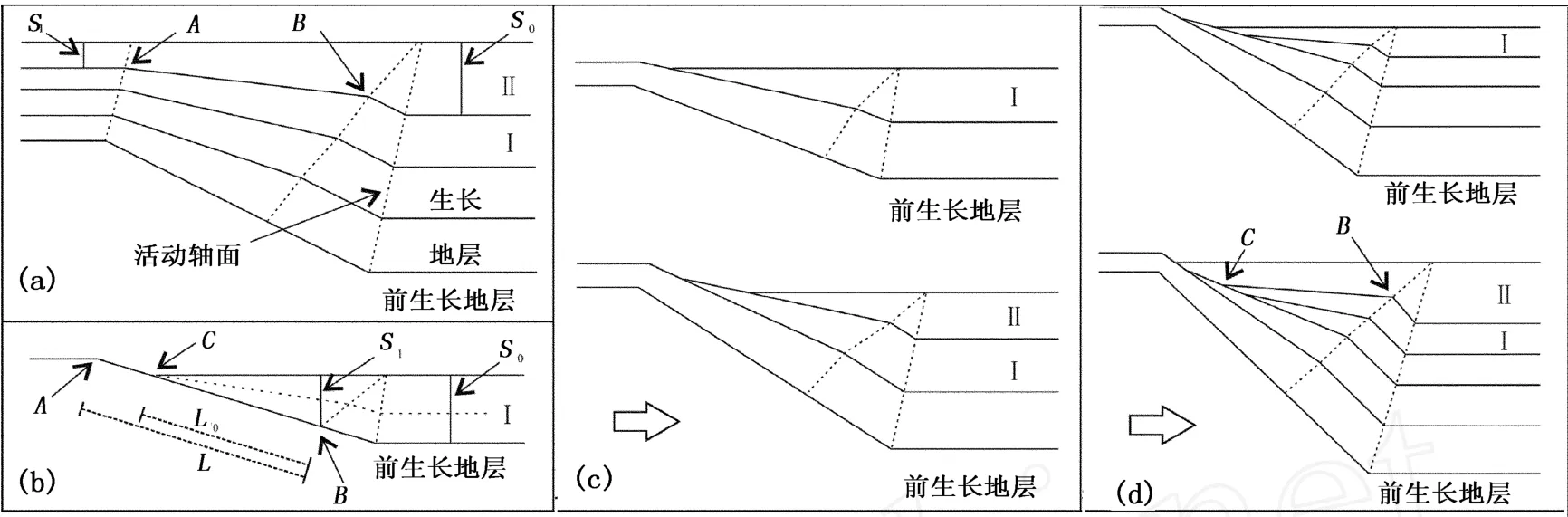
图 5 生长褶皱混合生长模式中生长地层的形态Fig.5 Growth strata patterns formed by hinge m igration with l imb rotation of growth fold

如图 5(a)所示,地层Ⅱ沉积过程中褶皱顶部的抬升量 U=S0-S1。在地层Ⅱ沉积期间,AB段上任一点的抬升由两部分组成,一部分由翼部旋转引起(U1),一部分由膝折带迁移引起 (U2)。由于 AB段位于膝折带上方,故其上各点经历了相同的膝折带迁移引起的抬升,即 U2为常数,而 U1呈线性变化,这样AB段上各点构造抬升仍具线性变化特征,形成楔状生长地层。

1.3.2 退 覆

如图 5(b)所示,地层Ⅰ沉积前,前生长地层水平。地层Ⅰ沉积期间,翼部一点 C的抬升速率与沉积速率相同成为尖灭点,故 C点抬升量等于盆地内地层Ⅰ的沉积厚度 S0。B点上地层Ⅰ的厚度为 S1,故B点的抬升量为 S0-S1。由前面的分析,AB段上各点构造抬升呈线性变化,褶皱顶部的抬升即 A点的抬升 U=S0+S1(L-L0)/L0。对于图 5(c),下伏为生长地层的退覆,也可用相似方法求出褶皱顶部的抬升量及抬升速率。

1.3.3 上 超

退覆之后的上超见图 5(d)。根据 B点和 C点上地层Ⅱ的厚度,计算出 B点和 C点的抬升量,进而由B点以上翼部各点构造抬升呈线性变化,可计算出褶皱的抬升量及抬升速率。

混合生长主要形成滑脱褶皱 (图 2(c))和剪切断层转折褶皱[16]。

2 讨 论

Suppe等[4]对断层转折褶皱中生长三角建立了如下公式:

保持与《劳动力创新和机会法》的一致性。新法案中使用的关键术语与《劳动力创新和机会法》中的术语相互呼应，并强调了职业与技术教育计划与《劳动力创新和机会法》计划之间在州和地方层面的协调。更重要的是，国会修改了法案的绩效指标，以更好地与《劳动力创新的机会法》中的绩效指标相匹配。

式中,vav为生长三角的平均生长速率,km/Ma;Lx,Ly,ΔL分别为已知年龄的两个地层单元褶皱翼部宽度及其改变量,km;Δt为两个地层单元年龄之差,Ma;tx,ty为两个地层单元的年龄,Ma。

利用式 (1)可以计算生长速率,进而划分构造形成期次。该式适用于膝折带迁移形成的断层相关褶皱。对于混合生长模式形成的褶皱,虽然也发育生长三角,但使用该公式分析褶皱过程会得到错误的结论,因此对于翼部旋转和混合生长两种模式形成的褶皱,式 (1)不适用。笔者提出的利用生长地层厚度推测褶皱抬升速率、褶皱过程,则涵盖了 3种模式。

利用式(1)计算生长速率时要求剖面必须垂直于构造线,否则将会产生误差,本文中采用的厚度分析则不要求剖面必须垂直于构造线。利用平衡剖面技术可以计算出地层的缩短率和缩短速率,这种缩短与褶皱抬升具有内在的联系,但它们之间并无直接的关联,不能用剖面的缩短来反映褶皱的过程。另外平衡剖面技术使用的“层拉平”,不允许出现地势高差,也限制了其精度,因此根据生长地层来推测褶皱过程是必要的。在根据生长地层厚度计算构造抬升速率时,为了提高可靠性,需对地层厚度进行去压实校正。

笔者进行厚度分析的前提条件是:水下环境,前生长地层水平 (构造抬升与沉积作用同时发生),沉积界面水平,不考虑侵蚀作用。前生长地层水平,这样生长地层可以记录下完整的褶皱过程;允许出现地势高差,这一点有别于断层生长指数的沉积完全补偿条件[17];沉积界面保持水平,这与短期内沉积作用实际受地形、搬运距离等多因素影响有差别,所以厚度分析时地层的时间单位以 1～10 Ma为宜[18]。在此条件下:当构造抬升速率小于沉积速率时,生长地层表现为上超和超覆,不会产生地形起伏,生长地层将完全覆盖褶皱,并完整地保存了褶皱变形的运动学特征;当构造抬升速率大于沉积速率时,生长地层表现为退覆,将引起地形起伏变化,只在背斜的两翼发生同构造沉积,部分记录了褶皱的运动学过程;当背斜顶部和向斜处地层厚度相同时,褶皱处于一个没有构造抬升的平静期[19-20]。

3 实例分析

以塔里木盆地库车坳陷为例进行分析。苏维依组、吉迪克组在全区厚度稳定,为前生长地层。康村组中后期克拉苏构造带南翼开始出现地层厚度变化,进入库车组后地层厚度变化更加明显,而此时南部的秋里塔格构造带地层仍相对稳定。西域组后秋里塔格构造带开始出现地层生长现象,而克拉苏构造带构造变形进一步加剧,其南翼地层生长现象更加明显,说明秋里塔格构造带的形成略晚于克拉苏构造带,构造应力具有自北向南迁移的特点。

克拉苏构造带南翼从康村组中后期开始,地震剖面上显示大量的超覆、退覆和上超现象,表明褶皱开始发育。时深转换后 (图 6)可以看出生长地层厚度总体呈线性变化,由于后期断层对褶皱的破坏和地震资料品质的限制,未能计算构造抬升速率。根据生长地层的分析,认为克拉苏构造带盐上层以盖层滑脱褶皱变形为主,早期为一高波长、波幅比的褶皱,其发育以翼部旋转为主,伴有部分膝折带迁移,库姆格列木群盐岩以前新生代发育的正断层(喀桑托开背斜)或基底倾角变化处 (库姆格列木背斜)为核聚集形成背斜,进一步地收缩,使不对称背斜 (库姆格列木背斜)的前翼和对称背斜 (喀桑托开背斜)的两翼发生断层突破,并使早期正断层反转、盐下层形成叠瓦构造。

图 6 克拉苏构造带 BC06-220测线地质剖面Fig.6 Geological profile of BC06-220 seism ic line in Kelasu tecton ic zone

4 结 论

(1)通过对生长褶皱进行详细的几何学分析并结合地层年代学资料,可以确定沉积速率与构造抬升速率的细微变化、褶皱的活动期次和褶皱形成的模式。

(2)以膝折带迁移模式形成的褶皱,发育过程中翼部倾角不变,褶皱顶部与翼部的抬升速率相同,形成翼部平行状生长地层。

(3)以翼部旋转模式形成的褶皱,发育过程中翼部长度不变,沿翼部各点的抬升速率呈线性变化,形成翼部楔状的生长地层。

(4)以混合生长模式形成的褶皱,发育过程中翼长和翼部倾角都发生变化,部分生长地层呈平行状,反映了膝折带迁移的特征,部分生长地层呈楔状,各点的抬升速率仍呈线性变化,反映了翼部旋转的特征。

[1] 叶兴树,王伟锋,戴俊生,等.东营凹陷沙三—东营期断裂活动特征 [J].中国石油大学学报:自然科学版,2006,30(4):7-11.

YE Xing-shu,WANGWei-feng,DA I Jun-sheng,et al.Characteristics of fault activities of Sha-3 member and Dongying periods in Dongying depression[J].Journal of China University of Petroleum(Edition of Natural Science),2006,30(4):7-11.

[2] KOSA E,HUNT D W.Growth of syndepositional faults in carbonate strata:Upper Permian Capitan platform,New Mexico,USA.[J].Journal of Structural Geology,2005,27(6):1069-1094.

[3] MEDWEDEFF D.Growth fault-bend folding at southeast Lost Hills,San Joaquin Valley,California[J].AAPG Bulletin,1989,73(1):54-67.

[4] SUPPE J,CHOU G T,HOOK S C.Rate of folding and faulting determined from growth strata[M]//MCCLAY K R.Thrust tectonics.New York:Chapman and Hall,1992:105-122.

[5] POBLET J,MCCLAY K,STORTI F,et al.Geometries of syntectonic sediments associated with single-layer detachment folds[J].Journalof Structural Geology,1997,19(3/4):369-381.

[6] STORTI F,POBLET J.Growth stratal architectures associated to decollement folds and fault-propagation folds.Inferences on fold kinematics[J]. Tectonophysics,1997,282(1/4):353-373.

[7] 王海荣,尚楠,高伯南,等.挠曲作用的形变响应及其识别特征 [J].中国石油大学学报:自然科学版,2008,32(5):22-27.

WANG Hai-rong,SHANGNan,GAO Bo-nan,et al.Deforming responses and its identification characteristics of flexing[J].Journal of China University of Petroleum(E-dition ofNatural Science),2008,32(5):22-27.

[8] 卢华复,贾东,陈楚铭,等.库车新生代构造性质和变形时间 [J].地学前缘,1999,6(4):215-221.

LU Hua-fu,JIA Dong,CHEN Chu-ming,et al.Nature and timing of the Kuqa Cenozoic structures[J].Earth Science Frontiers,1999,6(4):215-221.

[9] 刘志宏,卢华复,贾承造,等.库车再生前陆逆冲带造山运动时间、断层滑移速率的厘定及其意义 [J].石油勘探与开发,2000,27(1):12-15.

L IU Zhi-hong,LU Hua-fu,JIA Cheng-zao,et al.Orogeny t iming and fault-slip rate and their significance to the rejuvenated foreland thrusts beltof Kuche[J].Petroleum Exploration and Development,2000,27(1):12-15.

[10] 郭召杰,方世虎,张锐,等.生长地层及其在判断天山北缘前陆冲断褶皱带形成时间上的应用 [J].石油与天然气地质,2006,27(4):475-481.

GUO Zhao-jie,FANG Shi-hu,ZHANG Rui,et al.Growth strata and their application in timing defor mation of foreland thrust-fold belts in the north margin of Tianshan[J].Oil&Gas Geology,2006,27(4):475-481.

[11] 陈杰,WYRWOLL K H,卢演俦,等.祁连山北缘玉门砾岩的磁性地层年代与褶皱过程 [J].第四纪研究,2006,26(1):20-31.

CHEN Jie,WYRWOLL K H,LU Yan-chou,et al.Magnetochronology of the Yumen conglomerates and multi-pulsed folding and thrusting in the northernQilianshan[J].Quaternary Sciences,2006,26(1):20-31.

[12] 何登发,杨庚,管树巍,等.前陆盆地构造建模的原理与基本方法 [J].石油勘探与开发,2005,32(3):7-14.

HE Deng-fa,YANG Geng,GUAN Shu-wei,et al.Principles andmethodology of structuralmodeling in foreland basins[J].Petroleum Exploration and Development,2005,32(3):7-14.

[13] 王燮培,费琪,张家骅.石油勘探构造分析 [M].武汉:中国地质大学出版社,1990:80.

[14] POBLET J,MCCLAY K.Geometry and kinematics of single-layer detachment folds[J].AAPG Bulletin,1996,80(7):1085-1109.

[15] HARDY S,POBLET J.Geometric and numericalmodel of progressive limb rotation in detachment folds[J].Geology,1994,22(4):371-374.

[16] SUPPE J,CONNORS C D,ZHANG Y.Shear faultbend folding[M]//MCCLAY K R.Thrust Tectonics and Hydrocarbon Systems.AAPG Memoir 82,2004:303-323.

[17] HARDY S,POBLET J.The velocity description of defor mation,paper 2:sediment geometries associated with fault-bend and fault-propagagion folds[J].Marine and Petroleum Geology,1995,12(2):165-176.

[18] CASTELLTORT S,POCHAT S,DR IESSCHE J V.How reliable are growth strata in interpreting short-ter m(10 s to 100 s ka)growth structures kinematics?[J].C R Geoscience,2004,336(2):151-158.

[19] MASAFERRO J,BULNESM,POBLET J,et al.Episodic folding inferred from syntectonic carbonate sedimentation: the Santaren anticline,Bahamas foreland[J].Sedimentary Geology,2002,146(1/2):11-24.

[20] CASAS-SA INZA M,CORTE´SA L,MAESTRO A.Sequential limb rotation and kink-band migration recorded by growth strata,A lmaza’nBasin,North Spain[J].Sedi mentary Geology,2002,146(1/2):25-45.

Developmentmodels of growth fold

GUO Wei-xing1,2,Q IJia-fu1,2,L IMing-gang1,L I Yan-you1

(1.School of Resource and Infor m ation Technology in China University of Petroleum,Beijing102249,China;2.State Key Laboratory of Petroleum Resource and Prospecting in China University of Petroleum,Beijing102249,China)

Based on the kinematics characteristics of fold forming,the relationship between sedimentation and uplift of three kinds ofmodels including hinge migration,limb rotation and hinge migration with limb rotation was discussed.According to three kinds of developmentmodels of fold,a method was proposed to calculate fold uplift rate and folding process using the thickness of growth strata.The results show that the limb dip angle of fold developed by hinge migration keeps constant,and the fold has the same uplift rate in its crest and l imb.And parallel growth strata are formed.The l imb length of fold developed by limb rotation keeps constant,and the fold has the different uplift rate in its crest and limb,and the uplift rate changes linearly along the limb.Wedge-like geometry growth strata are formed.The limb length and limb dip angle of fold developed by hinge migration with limb rotation change in development.The lower parallel growth strata has the characterof hinge migration,while the upperwedge-like growth strata has the character of limb rotation.

tectonic uplift rate;sedimentation rate;hinge migration model;l imb rotation model;hinge migration with limb rotation model

P 542.2

A

1673-5005(2010)01-0001-06

2009-07-02

国家“973”项目 (2006CB202301)

郭卫星 (1978-),男 (汉族),河南新乡人,博士研究生,主要从事盆地构造分析方面的研究。

(编辑 徐会永)