基于FCM 和图割的交互式图像分割方法
2010-01-01田元,王乘,管涛
田 元, 王 乘, 管 涛
(华中科技大学数字化工程与仿真中心,湖北 武汉 430074)
交互式图像分割在医学图像处理、图像合成、影视技术、运动跟踪等领域具有广泛的用途。将人们对图像中的感兴趣的部分称为目标或前景,其他部分称为背景,交互式图像分割的目的就是把用户感兴趣的目标从图像中提取出来,以便作进一步的处理和分析。近年来,随着各学科许多理论和新方法的提出,人们也提出了一些新的分割方法,其中基于图论的交互式分割方法[1-3]引起了人们越来越多的兴趣。它的基本原理是将图像的分割问题转化为图的分割问题。首先,对用户选取的前景和背景分别进行分析,然后将未标记的点与前景和背景的相似性作为相似能量函数,用未标记点与其相邻点的相关性表示先验能量函数,将这两个能量函数作为判断该点属于前景或者背景的约束条件,最后利用最大流/最小割的方法求解能量函数的最优解。Boykov[1]等人提出利用灰度直方图的方法对前景背景的颜色分布进行分析,该方法对于前景背景颜色差别较大的图像的分割效果较好,但是当前景背景颜色相似时,其分割效果却不够令人满意。Li Yin[2]等人则提出了Lazy Snapping 方法,该方法利用K 均值聚类算法对前景和背景进行聚类分析。但是,为了获得更好的分割效果,该方法需要对分割后的图像进行进一步处理,即通过用户手动调整提取的图形的边界轮廓来获得更好的分割效果。
本文提出一种基于模糊C 均值聚类和图割的交互式图像分割方法,利用模糊C 均值聚类方法具有更好、更稳定的聚类性能,对用户选取的前景和背景分别进行分析,挖掘用户交互所提供的隐藏的提示信息,达到更准确的对未标记点进行分类的目的。同时,采用分水岭方法对图像进行预处理,将图像划分为多个区域,用区域代替像素点进行处理。与未经过手动调整的Lazy Snapping 方法相比,在相同的用户交互情况下,本文具有更好的分割性能,当图像中前景背景颜色相似时,更能体现本文算法的优越性。
1 基于图论的交互式图像分割方法

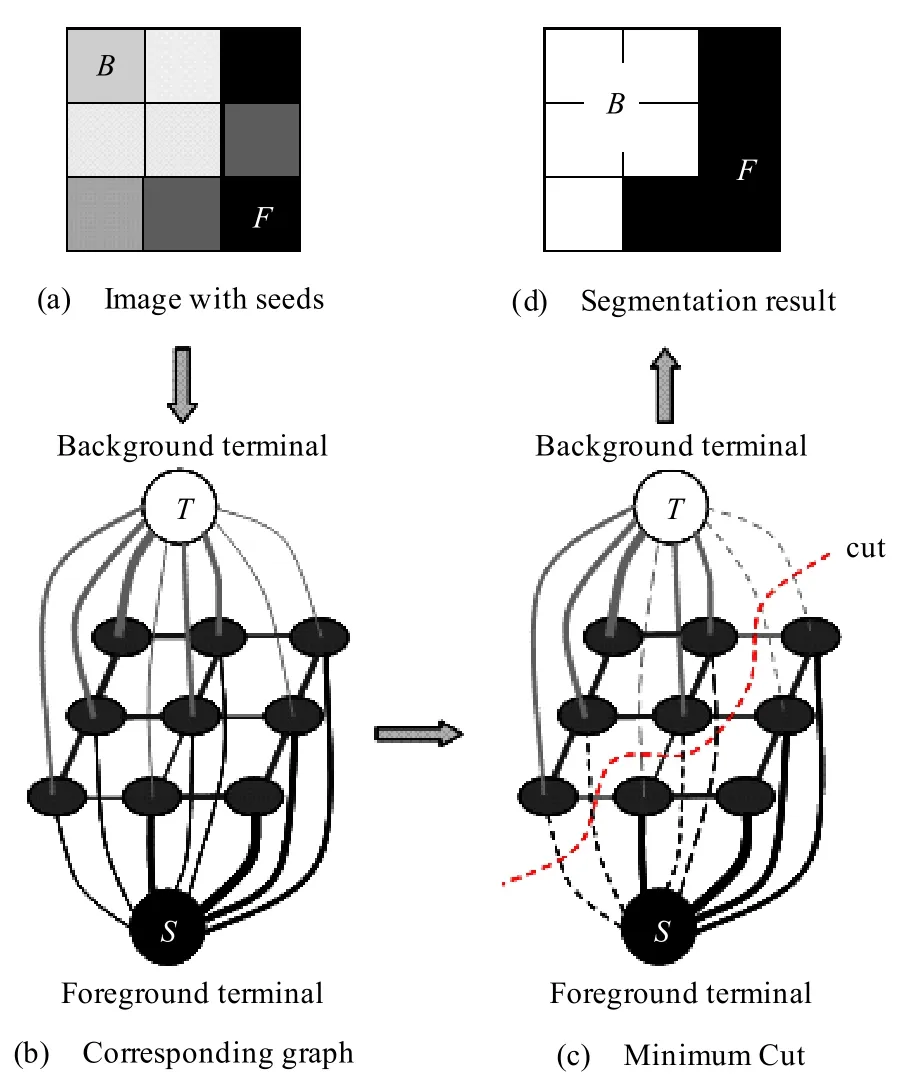
图1 3×3 图像分割示例
判断未标记的点属于F 类还是属于B 类,可以利用最大流/最小割算法求一个割集 EC ⊂ ,使割集中所有边的权值的和最小,其表达式为
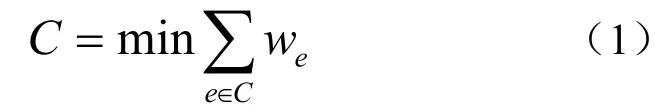
通过求图的最小割,图像中的像素被分为两类,且每个像素满足下列条件
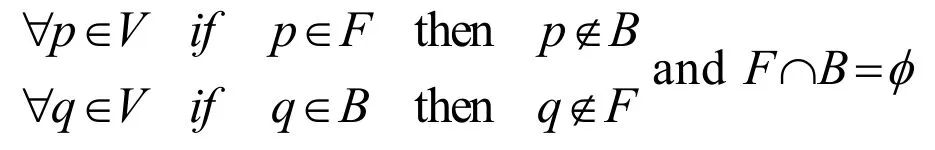
2 基于FCM 和图割的交互式图像分割方法
2.1 用分水岭算法对图像进行预处理
基于图割的图像分割方法的运行速度与图的节点数有密切的关系,图的节点数越少,分割速度越快。因此,本文采用分水岭算法对图像进行预处理,分水岭算法可以把图像中围绕区域极小点的像素聚类为一个一个的区域[4]。本文利用分水岭算法具有准确分割和精确定位图像边缘的特性,将图像分成多个小区域,然后,用区域代替像素点进行进一步分析,如图2 所示。这样,对于一幅大小为 N =Width ×Height 的图像,未经过预处理时,其节点数为N ,用分水岭算法对图像进行预分割后,图的节点数为M (M N≪ ),大大提高了算法的运行速度。
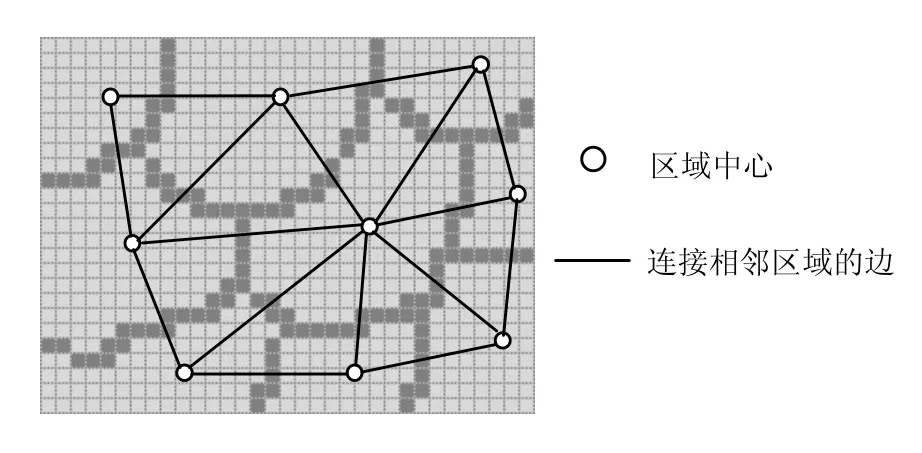
图2 用区域代替像素点进行分析
本文采用Vincent 等人给出的一种新的分水岭变换方法,此方法速度快、结果准确,具有实用价值[5]。Vincent 算法分为两步[4]:
(1) 排序 在逐渐淹没过程中,并非每次均需处理全部像素。为了能直接访问需要处理的像素,按像素灰度值的升序排列像素,得到一个排序后的像素矩阵,这样可以加速计算。
(2) 淹没 通过利用排序后的图像按图像像素灰度值升序地访问每一个像素来执行。对每一聚水盆地分配不同的标记,从整个图像的最小像素值开始,分配标记,依次淹没,利用先进先出的数据结构,即循环队列来扩展标记过的聚水盆地。通过一定的规则,分配分水岭标记,可以得到准确的结果。
2.2 用模糊C 均值方法对标记区域进行分析
模糊C 均值聚类算法是一种结合无监督聚类和模糊集合概念的方法[6]。不同于K 均值聚类算法将样本硬性的划分到某个类,模糊C 均值聚类方法允许某个样本不同程度同时归属于所有类,能更真实的反映自然界的模糊性和不确定 性[7]。因此,模糊C 均值聚类算法与传统的分级聚类算法、K 均值聚类算法相比,显示出更好、更稳定的聚类性能[8]。它的基本原理是,采用迭代法优化聚类损失函数来获得对数据集的模糊分类,在数学上可以表示为对目标函数求极值的问题。对于一幅大小为 Width× Height 的图像,其像素总数为 N =Width ×Height ,将整个图像分为C 类,即求下式中聚类损失函数J 的最小值[9]

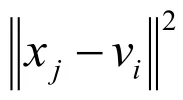
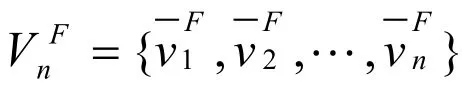
2.3 用图割法对未标记区域进行分类
用图割法对未标记的点进行分类,可以转化为利用最大流/最小割算法求解Gibbs能量函数[10]的全局最优解,其表达式为

其中 E1(vi)为相似能量函数,表示未标记区域的颜色与前景或背景颜色的相似程度,E2(vi,vj)为先验能量函数,表示未标记区域与其邻域的相关性。
本文中,相似能量函数 E1(vi)定义为
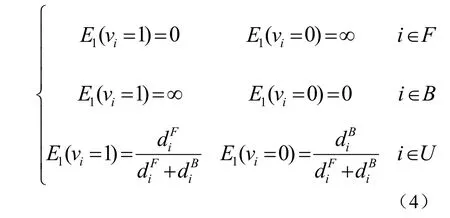
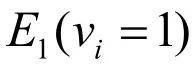
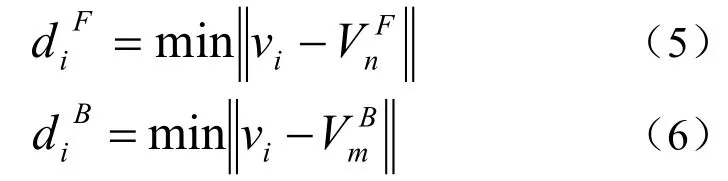
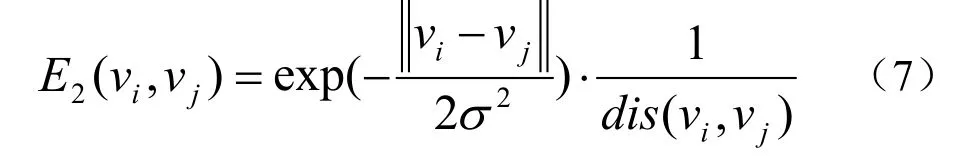
其中jv 为iv 的邻域, ),(jivvdis 为第i 个区域中心到第j 个区域中心的空间距离,σ 为摄像机噪声。区域iv 与其邻域jv 的颜色差别及空间距离越大,这两个区域被划分为同一类的可能性越小。反之,区域iv 与其邻域jv 的颜色差别及空间 距离越小,这两个区域被划分为同一类的可能性越大。
最后,利用最大流/最小割算法[11]求能量函数式(3)的全局最优解,达到将图像中的每个像素唯一的划分为前景或背景的目的。
3 实验结果及分析
本文算法在1.9GB 微处理器、512MB 内存、Windows XP 操作系统的环境下,使用VC6 实现。图3 为采用本文算法与Lazy Snapping 算法在相同交互条件下的分割结果的比较。图中用绿色标记前景,红色标记背景。图3 中,第一列为标记了前景和背景的图像,第二列为Lazy Snapping算法得到的分割结果,第三列为本文方法得到的分割结果,第四列为局部放大图。从分割效果可以看出,本文方法较Lazy Snapping 方法具有更好的分割性能,用户只需要在图像中分别选取感兴趣的物体和背景区域,就能从图像中提取目标物体,而且,当前景背景颜色相似时,本文的算法也能得到较好的分割效果。
[1] Yuri Y Boykov, Marie-Pierre Jolly. Interactive graph cuts for optimal boundary and region segmentation of objects in N-D images [C]//Proceedings of Internation Conference on Computer Vision, Vancouver, Canada, 2001: 105-112.
[2] Li Yin, Sun Jian, Chi-Keung Tang, et al. Lazy snapping[C]//Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, Los Angeles, 2004: 303-308.
[3] Hosaka T, Kobayashi T, Otsu N. Image segmentation using MAP-MRF estimation and support vector machine [J]. Interdisciplinary Information Sciences, 2007, 13(1): 33-42.
[4] 冯 林, 孙 焘, 吴振宇, 等. 基于分水岭变换和图论的图像分割方法[J]. 仪器仪表学报, 2008, 29(3): 649-653.
[5] Vincent L, Soille P. Watershed in digital spaces: an efficient algorithm based in immersion simulation [J]. IEEE Trans, PAMI, 1991, 13(6): 538-598.
[6] 刘晓龙, 张佑生, 谢 颖. 模拟退火与模糊C-均值聚类相结合的图像分割算法[J]. 工程图学学报, 2007, 28(1): 89-93.
[7] 蔡 涛, 徐国华, 徐筱龙. 基于模糊C 均值与Markov 随机场的图像分割[J]. 计算机工程, 2007, 33(20): 34-39.
[8] Mingoti S A, Lima J O. Comparing SOM neural network with fuzzy C-means, K-means and traditional hierarchical clustering algorithms [J]. European Journal of Operational Research, 2006, 174: 1742-1759.
[9] 边肇祺, 张学工. 模式识别(第2 版)[M]. 北京: 清华大学出版社, 2000. 280-282.
[10] Geman S, Geman D. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(6): 721-741.
[11] Yuri Boykov, Vladimir Kolmogorov. An experimental comparison of min-cut/max-flow algorithms for energy minimization in computer vision [C]// Proceedings of “EMMCVPR”, Sopgie Antipolis, France, 2001: 359-374.

图3 本文算法与Lazy Snapping 算法的分割结果比较
