弧面凸轮分度机构设计及建模方法研究

方代正 ， 王贵成

（1. 江苏大学机械工程学院，江苏 镇江 212013； 2. 安徽理工大学机械工程学院，安徽 淮南 232001）

弧面凸轮分度机构可由一个凸轮机构实现简单的间歇运动，也可将两种以上凸轮组合起来，实现许多复杂形式的转动或移动。它具有高速、重载、高精度、长寿命、高效率、结构紧凑、传动平稳，传递转矩大，动力特性好等优点，被广泛应用在食品、印染、印刷、包装、冲压、电子和机器人等机械中。目前对圆柱滚子和圆锥滚子的弧面凸轮分度机构研究较多，但以钢球作为滚子的研究不常见，笔者将D-H 坐标系引入该机构，建立其数学模型，然后用Pro/E 进行三维造型，为以后进行加工、分析、仿真作好准备。

1 基于D-H 坐标建立啮合方程

1.1 机构工作原理

钢球滚子弧面凸轮分度机构的结构如图1 所示，由凸轮轴，分度盘，钢球，机座，环形轨道等组成。以凸轮轴为主动输入，凸轮轴与装在从动盘上的钢球相啮合，当凸轮轴转动时，便推动钢球滚动，从而带动从动盘转动[1-3]。

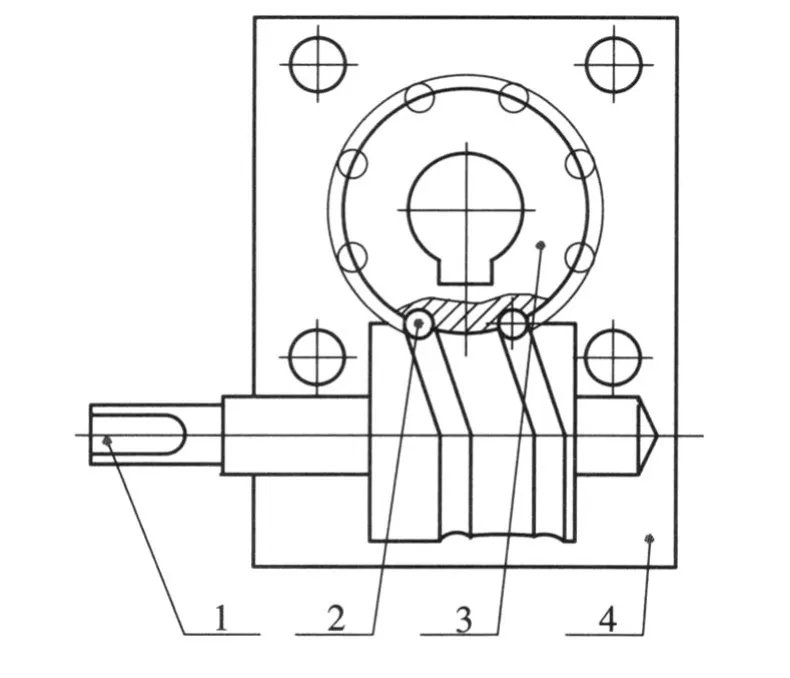
图1 弧面凸轮钢球式分度机构原理图

1.2 D-H 坐标系简介

D-H 坐标系由Denavit 和Hatenberg 提出，通常用来描述机械手的惯用坐标。D-H 坐标系规定： 在机械手的各个主要构件上固定有坐标系。坐标系的Z 轴可取得与运动副的轴线重合，X 轴则沿着相邻两个Z 轴的公垂线，而Y 轴可由右手笛卡尔法则来确定。

Denavit 和Hatenberg 提出的机器人相邻连杆间的位姿坐标转换关系为

其中 C、S 分别表示cos、sin。1nα−为从 1nz−到zn绕 xn−1旋转的角度；dn为从 xn−1到 xn沿 zn方向的距离；nθ 为从 1nx−到nx 绕nz 旋转的角度；αn−1为从 zn−1到 zn沿 xn−1方向的距离；将第n 关 节前的坐标转换式相乘得到第n 关节相对于基础坐标系的转换式

1.3 根据D-H法弧面分度凸轮轮廓和啮合方程的建立

根据D-H 法可以建立弧面分度凸轮机构的坐标系如图2 所示，各参数意义说明如下[4-6]：

图2 D－H 坐标系的建立

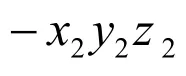
ϕf,ψf：球形滚子的工作曲面参数； lf：从动件的回转半径；

θ1、 θ2：分别为凸轮和从动件所对应的转角；12,ω ω ：分别是凸轮和从动件相应的角速度。

根据图中对应的关系，易知球形滚子在从动件坐标系中的向量表达式为

根据上图所建立的弧面凸轮分度机构的坐标体系，容易求得4 个坐标系之间的相互变化矩阵，各齐次变换矩阵分别为式（4）～式（6）

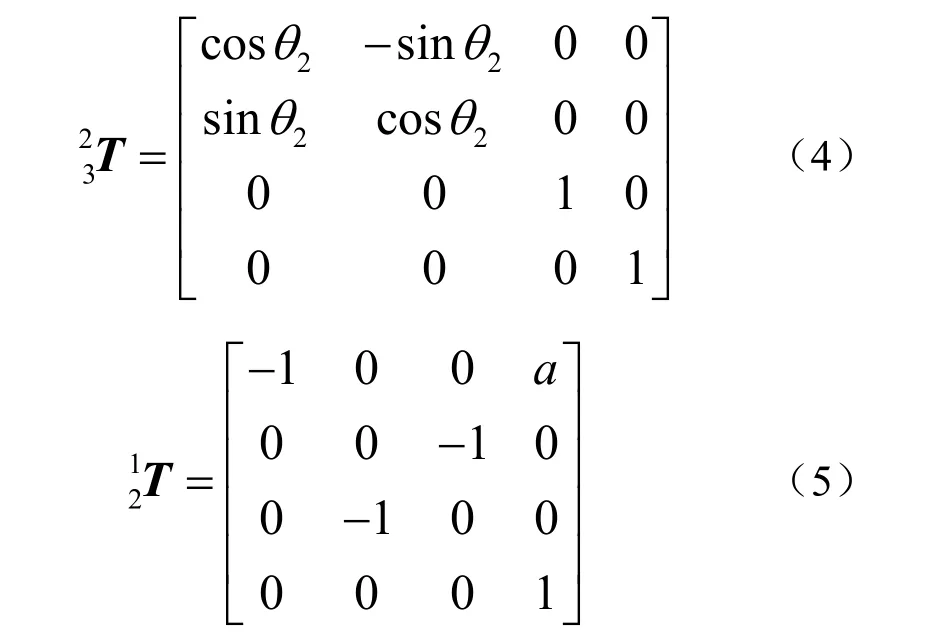
将从动件坐标系中球形滚子的向量表达式通过坐标变换转换到凸轮坐标系中，实际上得到弧面凸轮分度机构的曲面方程

其中

表达式中的滚子曲面参数 ϕf,ψf可以通过空间 啮合条件进行求解。

1.4 共轭接触方程

根据空间啮合条件式

将有关表达式代入式（9），计算并化简得到

基于微分几何的相关理论，与啮合点的切平面垂直的矢量称为曲面在啮合点的单位法向矢量，有

将式(10)和式(12)代入式(8)并整理得到

联立式(7)和式(13)就可求解出空间凸轮啮合接触线的方程。

2 弧面凸轮的建模

现在三维造型软件比较多，造型方法各异，常用的造型软件有Pro/E 、UG、SolidWork等，即使同一种软件造型过程不同其难易程度和精度也不一样。弧面分度凸轮的工作廓面是空间不可展曲面，其设计与制造都比较困难，因此，如果能在加工之前应用软件将弧面分度凸轮的三维模型制作出来，对其进行仿真分析等，就可以验证设计过程是否正确，一旦设计有误可以提前及时修改[7-10]。

已知实际条件：凸轮转速n＝150r/min，连续旋转，从动盘上均布有8个滚子，中心距C=80mm，该弧面凸轮的运动规律采用的是修正正弦曲线。

通常基于Pro/E 利用文件生成高级曲面来创建弧面分度凸轮的三维模型采用以下两种方法：

方法一：利用文件创建弧面分度凸轮曲面。根据弧面凸轮接触方程和分度机构的相关参数利用计算机语言自动计算出凸轮轮廓表面一系列的坐标数据，再导入文本文件，通过文本文件的数据点来建立弧面凸轮的曲面。

方法二：利用方程创建弧面分度凸轮曲面。根据凸轮曲线的运动规律，随参数的取值大小不同，在各段生成符合要求的一组曲线，将各段的曲线依次混合成曲面，再将各个曲面合并成一个曲面，最后将曲面实体化，生成所需要的弧面凸轮[8]。

以上两种方法虽然能最终生成弧面凸轮实体，但计算工作量都比较大，而且最后精度与计算过程中所取的步长直接有关。众所周知，弧面凸轮的滚子形式常见的有圆柱滚子、圆锥滚子，鼓形滚子，球形滚子等，不论是哪种形式的滚子，都具有一个对称面，在运动过程中可看成始终沿着对称面上的一条线进行移动，而球形滚子更为特殊，这条线就是经过球心的中心线。在造型过程中充分利用这一特征可以使弧面凸轮的造型变得十分简便，而且精度高，其精度是有软件自身运行精度所决定，不受人为所取步长的大小影响。具体操作步骤如下：

（1） 生成凸轮基体 由已知数据，可先计算出凸轮的基圆半径和凸轮的宽度，利用旋转工具生成凸轮基体，见图3所示。

图 3 凸轮基体

（2） 生成中心轨迹线 由于滚子形式是钢球，其运动轨迹是半圆形环状包络线。通常情况下，随着球的几何参数取值不同，可形成一组曲线，然后由曲线混合成曲面。但也可以先生成中心线轨迹，利用混合扫描，沿着中心线轨迹也可以生成弧面凸轮。圆上任意相隔180°的两点关于圆心是对称的，因此，在选取球的角度参数时，任取相隔180°的角度参数生成关于中心线对称的两条线，而取平均值就会生成中心线轨迹。在生成过程中，中心线轨迹是分段曲线，可以逐段混合扫描去除材料，也可以将分段的中心线合并成一条曲线，最后再扫描，但这时会占用大量计算机内存，运行时间较长。见图4所示。

图 4 滚子中心线轨迹

（3） 利用混合扫描工具 绘制半圆形的截面，沿中心线轨迹切除材料，就可生成弧面凸轮轮廓面的三维模型，见图5所示。

图 5 沿中心线轨迹的混合扫描图

（4） 对一些棱边进行倒角或倒圆处理 最终生成的弧面凸轮实体如图6所示。

图 6 弧面凸轮的三维模型

3 结 论

（1） 建立弧面凸轮分度机构的数学模型的方法有多种，但复杂程度不一样，文中利用D-H坐标系来建立球形滚子弧面凸轮分度机构的数学模型，这与笔者之前采用的回转张量法等其它方法得到的结果是一致的，但D-H 方法显得更简单明了，减少了计算工作量。

（2） 在造型过程中要根据球形滚子的几何特征，利用沿中心轨迹线混合扫描来生成弧面凸轮，比采用其它方法要简便得多，而且更精确、快速，从而为下一步利用数控加工进行编程、对机构进行动力学分析和运动仿真奠定基础，以便判断所设计的机构的合理性。对其它形式的滚子，也可以采用类似的方法进行造型。

[1] Der Min Tsay, Hui Chun Ho, Kuan Chang Wang. Design of torque balancing cams for globoidal cam indexing mechanisms [J]. ASME J. of Mech. Des., 2002, 124(3)： 441-447.

[2] 彭国勋, 肖正扬. 自动机械的凸轮机构设计[M]. 北京： 机械工业出版社, 1990. 114-154.

[3] Fu Yanming. Analysis and design of the globoidal indexing cam mechanism [J]. Journal of Shanghai University (English Edition), 2000, 4(1)： 54-59.

[4] 张高峰, 杨世平, 陈华章, 等. D-H 方法在弧面分度凸轮机构设计中的应用[J]. 机械传动, 2003, 27(4)： 46-49.

[5] Tsay D M, Ho H C. Consideration of manufacturing parameters in the design of grooved globoedal cam indexing mechanisms [J]. J. Mech. Eng. Sci., 2001, 215(1)： 95-103.

[6] 何 仁, 董 颍, 罗福强. 发动机缓速器减压凸轮的设计[J]. 江苏大学学报(自然科学版), 2007, 28(2)： 111-114.

[7] Tsay D M, Huang M H, Ho H C. Producing follower motions through their digitized cam contours [J]. ASME J. Computing and Information Science of Engineering, 2002, 2(6)： 98-105.

[8] 胡文祥. 基于Pro/ENGINEER 平台的弧面分度凸轮特征造型[J]. 制造技术与机床, 2006, (7)： 36-49.

[9] 王清仙, 郭 慧, 马永有. 一种自由曲面零件的反求方法[J]. 江苏大学学报(自然科学版), 2006, 27(5A)： 49-51.

[10] Hong-sen Yan, Hsin-hung Chen. Geometry desing of roller gear cams with hyperboloid rollers [J]. Mathl. Comput. Modelling, 1995, 22(8)： 107-117.