基于多种群实数编码遗传算法的圆度误差评定

缪立栋， 郭 慧， 张 帆

（华东理工大学机械与动力工程学院，上海 200237）

圆度误差是指回转体在同一正截面上实际被测轮廓相对其理想圆的变动量。它是衡量圆柱形零件形状精度的重要指标之一，误差的大小将严重影响其工作性能。在GB7234—87（圆度测量术语、定义及参数）中，圆度误差的评定方法有：最小区域圆法、最小二乘圆法、最小外接圆法和最大内接圆法。用最小区域圆评定准则所评定的圆度误差值为最小，且具有唯一性。我国标准规定圆度误差必须按最小区域圆评定准则进行评定[1]。

按最小区域法评定圆度误差，关键是如何找到相夹被测轮廓且半径差最小的两同心圆。这种评定方法实际是最优化问题，采用遗传算法进行计算可以准确快速的找到最优解。遗传算法作为一种全局收敛算法，较之优化迭代算法如单纯形法，Gauss-Newton 法、levenberg-Marquart 法，已证明能够较为准确，有效搜索到全局最优解。但是，仍存在而收敛速度慢、效率不高、局部收敛及精度不高等问题。

本文在实数编码(RGA)的遗传算法的基础上，运用遗传算法自有的并行性，对算法进行了改进，引入多种群遗传算法，通过实验对比，证明多种群实数编码遗传算法(RMGA)有效的提高了全局搜索能力和局部搜索速度，收敛更快，精度更高。

1 多种群遗传算法(RMGA)

1.1 遗传算法(RGA)的不足

遗传算法是一种借鉴生物界自然选择机制和自然遗传机制的随机化搜索算法，该算法中种群规模的大小、交叉率、变异率的选取，各染色体适应度函数值的相对大小，以及收敛条件的设定等，对优化结果以及收敛速度都有一定影响。

但常用的简单遗传算法(RGA)往往存在着不易成熟收敛[2]的现象，主要表现在群体中的所有个体都趋于同一状态而停止进化，算法最终不能给出令人满意的解。未成熟收敛的发生主要和下列几个方面有关：

（1） 在选择操作过程中。当群体中存在适应度比其他个体高得多的个体时，该个体将会多次被选中，下一代群体很快被该个体所控制，群体失去竞争性，使问题过早地收敛于局部解。

（2） 交叉和变异操作中。交叉概率Pτ、变异概率Pm取值不当极容易收敛于局部解。且不同的问题所对应的最佳Pτ、Pm取值往往不同，每个问题都要通过不断的反复试验才可确定，效率低下。

（3） 当群体规模较小时，群体中多样性程度低，个体间竞争较弱。群体易趋于单一化，交叉操作的作用渐趋消失，群体的更新仅靠变异操作来维持，群体将很快收敛于局部最优解；当群体规模较大时，势必造成计算量的增加，计算效率受到影响。

（4） 如果规定的最大遗传代数过少，进化不充分，也会造成未成熟收敛。

1.2 改进的多种群遗传算法(RMGA)

针对简单遗传算法所存在的上述问题，为克服未成熟收敛，本文应用了一种算法性能更好的遗传算法模型——多种群遗传算法结构模型[3]（简称RMGA），可以用来取代常规的标准计算模型。RMGA 在RGA 的基础上主要引入了以下几个概念：

（1） 突破RGA 仅靠单个群体进行遗传进化的框架，引入多个种群同时进行优化搜索；

（2） 各个种群之间通过迁移因子进行联系，实现多种群的协同进化；最优解的获取是多个种群协同进化的综合结果；

（3） 在进化收敛后，在全部种群的所有个体之间选择适应度函数最大的个体作为最优解。多种群遗传算法的结构（以3个种群为例）如图1所示。

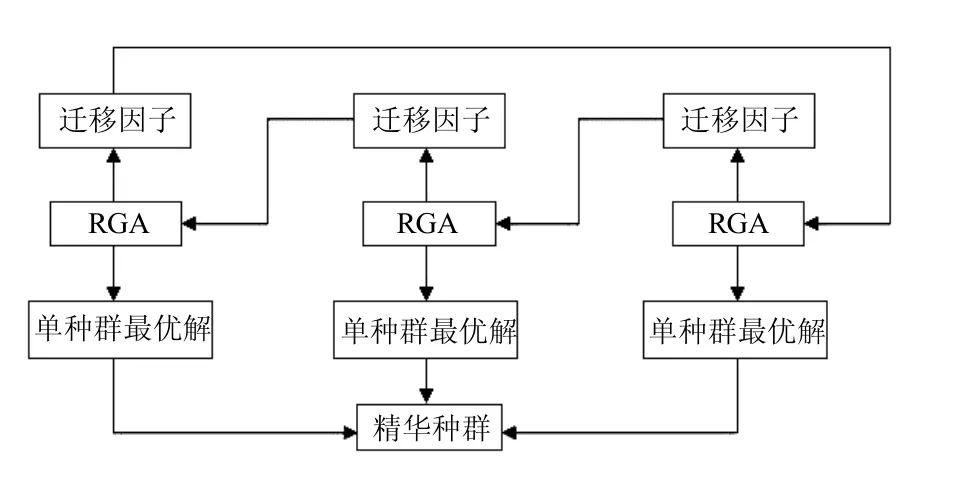
图 1 多种群算法结构示意图

因为有3个种群同时对解空间进行协同搜索，群体的多样性由3个种群协同维持，故各种群的群体规模可以减小。多种群中的精华种群和其他种群有很大不同。在进化的每一代，将各个种群的最优个体放入精华种群加以保存。精华种群不进行选择、交叉、变异等遗传操作，保证进化过程中各种群产生的最优个体不被破坏和丢失。同时，判断算法终止条件在精华种群中产生，收敛判据是精华种群中最优个体适应值连续保持不变的最大代数和最大遗传代数相结合，这样比RGA 收敛判据更合理。

1.3 多种群遗传算法的具体步骤[4-5]

（1） 根据圆度误差测试数据给出圆心坐标，即染色体(x, y)的解域范围，可以根据经验或者通过传统算法给出；

（2） 确定子种群数量及子种群的初始群体数量Ni，交叉概率Pτ以及变异概率Pm、子种群迁移率、最大进化代数；

（3） 计算每一个体的适应度函数，适应度函数采用如下线性函数

式中 Ni为种群的大小，P 根据目标函数式(5)的大小所确定的个体在种群中的位置；sp 为选择压力，1≤sp≤2；所以一般取sp=1.7；

（4） 每个子群分别独立采用遗传算法进行复制、交叉、变异操作，子种群每进化若干代就进行子群间的迁移；

（5） 选择操作：将种群中的个体按适应度由大到小排序，然后根据单个个体所对应的适应度确定其繁殖后在交配池中所占比例

（6） 交叉操作：操作是遗传算法中最主要的操作，这里采用算术交叉方式产生后代，按照线性组合，产生新的个体，公式为

其中 Xi、Xi+1分别为父代的第i 个和第i+1个变 量，iX′，1i+X′ 分别为新产生的子代的第i 个和第 i +1个变量，r {0,∈ 1}为均匀分布的随机变量。

（7） 变异操作：随机的选取一个个体，并随机的使其中1个参数在其取值范围内随机的增加或者减少5%；

（8） 种群是否达到最大进化代数，如果未达到就转向步骤(4)。否则此时选出全体种群中适应度最大的个体所对应的目标函数值，即为全局最优解。

算法程序框图如图2所示。

图 2 多种群遗传算法程序框图

2 圆度误差评定的数学模型

圆度误差是指被测实际圆对其理想圆的变动量，理想圆的选择应使变动量为最小。其表示方法是用两同心几何圆将实际圆包容在中间，当两几何圆的间隙为最小时，该两几何圆半径之差即实际圆的圆度误差[1]，如图3所示。圆度的误差带的大小和位置是一个待定的浮动区域。

图 3 圆度误差

圆度误差值的评定按其定义应为最小区域圆法(MZC)，近似的评定方法有最小二乘圆法(LSC)，另外有最大内切圆(MIC)方法，最小外接圆(MCC)方法。不同的方法，对应不同中心的理想圆。

圆度误差是衡量圆形零件形状精度的重要指标之一，按最小区域法来计算圆度误差是一个非线性优化问题，已有的方法受到计算精度的限制。

为了提高算法精度和收敛速度，快速准确评定圆度误差，本文运用RMGA方法通过多个子种群计算并迁移优良个体的进化过程来实现对理想圆圆心以及圆度误差的快速搜索。

设实际圆周上测量点的坐标值为 mi( xi,yi) (i=1, 2,…, n)，n为测点数，理想圆的圆心位置为m ( x, y )，则测量点到理想圆圆心的距离为

按最小区域法评定圆度误差，实质上是寻找包容被测实际圆且具有半径差为最小的两理想同心圆，包容被测轮廓的同心圆有无数对，但只有一对半径差是最小的，这对同心圆的圆心即为所求。

根据最小区域要求，圆度误差为

式(5)即为用RMGA方法求解满足最小区域 要求圆度误差的目标函数，优化变量为使 ( )

f x,y最小的x 和y，圆度误差的评定转化为求二元函数 f ( x,y )的最小值问题。

3 计算实例

以文献[6]中圆度的测量数据为例（见表1）进行误差计算分别采用实数编码遗传算法(RGA)和实数编码多种群(RMGA)方法计算圆度误差，RMGA方法计算圆度误差时参数设置为：种群范围[0，0.1]，子种群数为4，每个种群的个体数目20，采用离散重组，变异率0.2，最大进化次数60，迁移率0.2，在5代之间发生迁移，代沟0.8。RGA方法的参数设置为：种群范围[0，0.1]，个体数目80，采用离散重组，变异率0.2，最大进化次数60，迁移率0.2，代沟0.8。

RMGA方法进化过程如图4所示，计算结果列于表2中，并将文献[6]最小区域法的求解结果一并列入表中以便比较。同时，应用RGA方法对表1的数据进行计算，计算结果列入表2中，迭代曲线如图5所示。

图 4 圆度误差的RMGA迭代曲线

表1 圆度误差计算的数据测量[6]

图 5 圆度误差的RGA迭代曲线

表 2 圆度误差计算结果的比较

比较表2的结果可知，RMGA 方法的结果优于文献[6]的最小区域法结果和RGA 方法的结果。从图4可知RMGA 进化计算很快获得最优解，RMGA 方法在30多代以后就已经基本收敛，RGA方法在40多代以后还在波动，说明RMGA 方法比RGA 方法有更快的收敛速度，用于计算圆度误差是很有效的。

4 结 论

本文针对遗传算法所存在的早熟收敛、精度不高、计算效率低等缺点。分析了原因，并借助遗传算法的并行性，引入多个种群对算法过程进行改进。通过实例计算，对实数编码遗传算法和多种群遗传算法进行试验比较。实验表明改进后的多种群遗传算法能有效克服原算法缺点，有效地收敛到全局最优解，提高了收敛速度和精度，该算法同时也能够给其他形位误差的评定提供参考。

[1] 甘立永. 形状和位置误差检测[M]. 北京： 国防工业出版社, 1995. 73-94.

[2] Sbrizzai R, Torelli F. A pipelined—in—time parallel algorithm for transient stability analysis [J]. IEEE Transactions on Power Systems, 1991, 6(2)： 715-722.

[3] Potts J C, Giddens T D, Yadav S B. The development and evaluation of an improved genetic algorithms based on migration and artificial selection [J]. IEEE Trans on SMC. 1994, 24(1)： 73-86.

[4] 邹 琳, 夏巨谌, 胡国安. 基于实数编码的多种群并行遗传算法研究[J]. 小型微型计算机系统, 2004, 25(6)： 982-986.

[5] 刘 勇, 康立山, 等. 非数值并行算法(第2册)[M].北京： 科学出版社, 1995. 108-120.

[6] Huang J. A new strategy for circularity problems [J]. Precision Engineering, 2001, 25： 301-308.