三角域上C1 连续的H-Coons 曲面片
2010-01-01唐运梅吴晓勤韩旭里
唐运梅, 吴晓勤,韩旭里
(1. 湖南科技大学数学与计算科学学院,湖南 湘潭 411201; 2. 中南大学数学科学与计算技术学院,湖南 长沙 410083)
曲面造型是CAD/CAM 的核心技术之一,它所追求的目标是能够灵活、方便地设计出所需的各种各样复杂的形状。三角域上的曲面造型方法能有效地解决构型复杂、形状和边界不规则产品的几何造型问题,是对散乱数据进行曲面插值的基础。
在三角形域上,通过对边界曲线插值来构造三角曲面片的方法最早是由Barnhill, Birkhoff 和Gordon[1]提出的,该方法采用布尔和算子构造三角曲面片;并且要求给定的插值条件满足相容性。如果给定的插值条件不满足相容性,则所构造的三角曲面片上还需加上一个修正项,以去掉不相容性[2-3]。Gregory[4-6]使用凸组合的方法构造三角曲面片,所构造的三角曲面片由3 个插值算子的凸组合构成,每个插值算子均满足三角形两条边上的插值条件。Nielson[8]提出的边-点法也使用3 个插值算子的凸组合构造三角曲面片,每个算子满足一个点及其对边上的插值条件。Hagen[9]进一步发展了边点法,并用来构造几何三角曲面片。这些研究结果已被一般化为构造具有一阶或二阶几何连续的三角曲面片的方法[10-11]。徐琳[12]对现有的三角域上的超限插值方法进行了综述。
随着几何造型工业的发展,往往要求调整曲面的形状或改变曲面的位置。Barsky[13]通过在基 函数中引进了两个参数首先引入了β -样条曲 线,用以调整曲线的形状。近年来,许多学者在不同的函数空间中引入参数得到了一些新的曲 线。 Zhang[14]通 过 引 入 角 度 参 数α , 在{1 ,t ,sint,cost}找到了三组不同的基函数,构造 的曲线作者称之为C-曲线,包括C-Ferguson 曲线、C-Bézier 曲线、C-B 样条曲线。最近,不少学者用双曲多项式代替三角多项式,得到了一些新的曲线;汪国昭等[15]讨论了平面三次混合双曲多项式曲线及其形状分类,提出了三次H-Bézier曲线,其后文献[16-17]研究了一般的n 次H-Bézier 曲线; 文献[18]讨论了均匀的双曲多项式B 样条曲线。H-Bézier 曲线和H-B 样条曲线除了具有Bézier 曲线和B 样条曲线类似的性质外,可精确表示双曲线和悬链线;且跟C-Bézier曲线和C-B 样条曲线相比,一是参数α 的取值范围更大,二是更逼近控制多边形。带有形状参数的曲线,运用张量积方法很自然推广到矩形域的曲面上;但在三角形域上如何构造带有形状参数的曲面,至今研究的文献不多。
大家知道Coons方法也是计算机辅助几何设计和计算机图形学中一种构造曲面的重要方法。本文讨论在三角形域上如何构造C1连续的H-型Coons 曲面片。首先给出两种类型的双曲混合型的Hermite 多项式,称之为H-Hermite 多项式。然后将文献[1]边-边方法,与Nielson 边-点方法的Hermite 多项式用不同的H-Hermite 多项式替换得到了三种C1连续插值边界数据的三角曲面片。构造的三角曲面片均含有形状参数α ,调整α 的值,可改变曲面的内部形状,而不影响曲面的边界形状,当α 0→ 时,可退化为通常的边-边与边-点方法插值的曲面片。最后,实例显示了本文方法的实际效果。
1 H-Hermite 多项式
1.1 第一类H-Hermite 多项式
类似于Zhang[14]在1996 年给出了C-Hermite多项式,作者给出第一类H-Hermite 多项式。
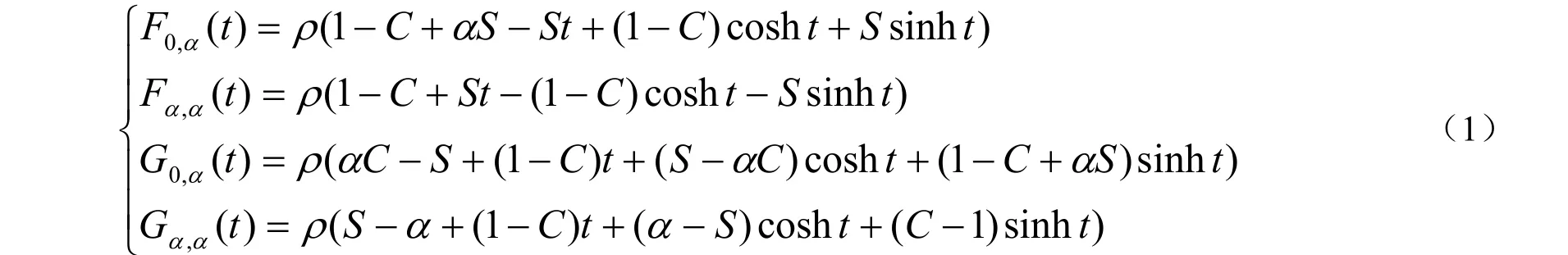
其中 α∈ (0 ,+∞),0 ≤t ≤α , S =sinhα, C =cosh α, ρ=1/(2−2C +αS)。
第一类H-Hermite 多项式具有三次Hermite多项式类似的性质
i, j=0,α
其中 δij为克罗内克符号。
为了在三角域上讨论插值问题,须作变换 t = αu,使得 u ∈[0,1],这样有

易见,式(2)具有三次Hermite 多项的性质。
1.2 第二类H-Hermite 多项式
下面给出第二种类型的H-Hermite 多项式

其中 α ∈ (0, +∞ ),0 ≤t ≤α , S =sinhα, C =coshα, ρ=1/(2−2C +αS )。
简单计算可验证第二类H-Hermite 多项式具有性质

同样,通过变换 ut α= ,使得 ]1,0[∈u ,有
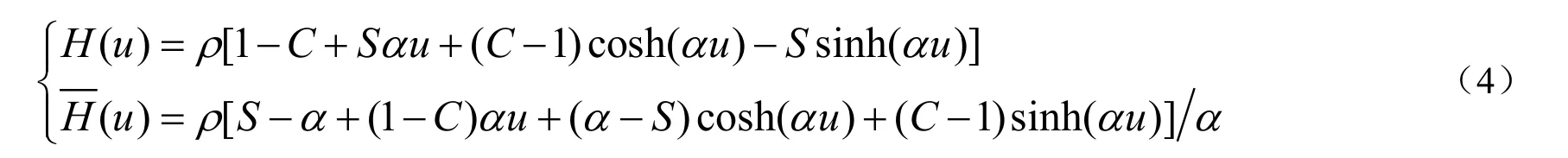
可验证式(4)有性质

2 三角域上C-曲面片
在三角域上对其边界数据进行超限插值时,宜选用重心坐标。在以下的讨论中,为了记号方 便,总假定 i,j,k = 1,2,3,i ≠j≠k≠i。
2.1 重心坐标
设T 表示一非退化的三角形,其顶点为Vi( xi,yi)( i =1,2,3),顶点按逆时针方向标号。记 ei为顶点 Vi所对应的边,即 e1= V3−V2,e2=V1−V3, e3= V2−V1;△T 的边界记为∂T 。如图1 所示,点P 为三角形T 内任一点,记点P 关于△T 的重心坐标记为 (b1,b2,b3),则bi= Ai/A,其中A 为△T 的面积,Ai为△ PVjVk的面积。

图1 点P 在△T 的重心坐标
2.2 边-边插值方法
所谓边-边插值方法是:先采用BBG[1]的平行投影方法,构造插值三角形的两条边界数据的曲面片,再将三张插值曲面片凸组合得到插值三条边界数据的曲面片。
设 ),( yxF 为一给定的二元函数,iP 为一基本插值算子,它插值边界上两点及沿着方向ie 的跨界导矢,算子的具体表达式可参考文献[7],图2 给出了1P 插值说明。
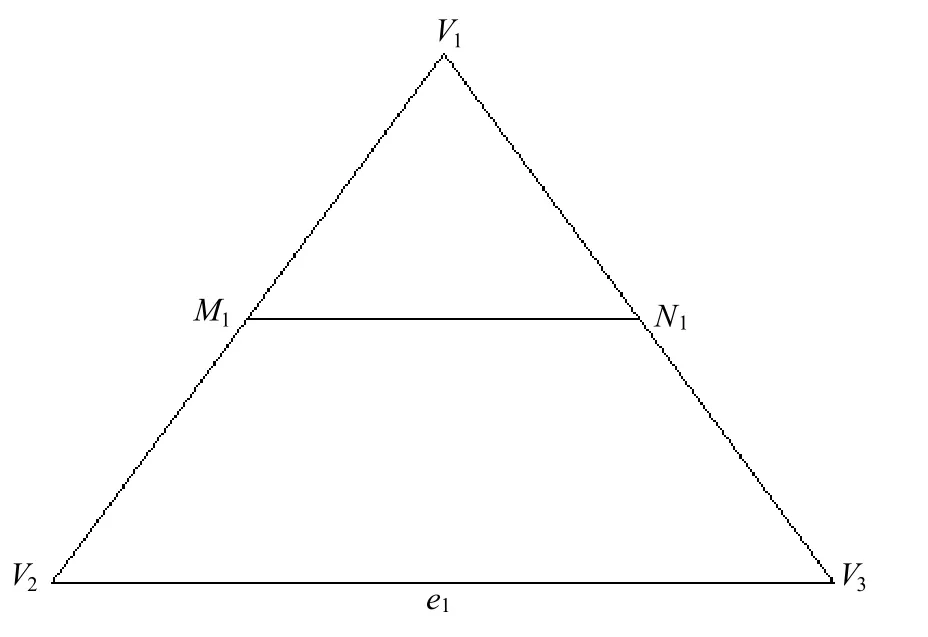
图2 P1[F]插值的几何解释
现将基本插值算子iP 中的三次Hermite 多项式用第一类H-Hermite 多项式替换,有
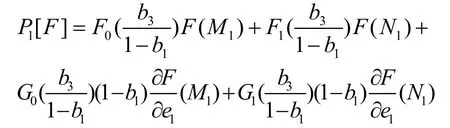
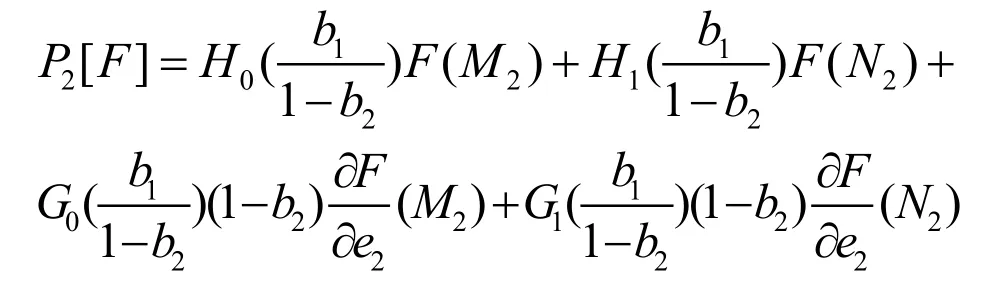

用Gregory[6]方法将 P1[F]、 P2[F]、P3[F]凸组合定义曲面如下
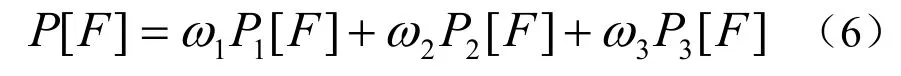
其中 ωi( i=1,2,3)称为权函数(或混合函数)。
为了保证 P[ F]的C1插值特性,可选取
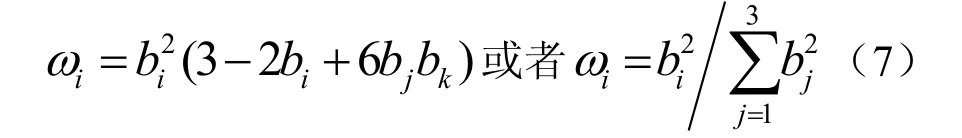
上述的权函数具有性质:

定理1 若 ),( yxF )(1 TC ∂∈ ,则当 Tyx ∂∈),(时, ][FP 插值 ),( yxF 及其一阶导矢。
证 明由基本插值算子 P1[F]、 P2[F]、P3[F]知,它们分别插值三角形上两条边上的函 数值和一阶导矢值;再由权函数的性质即可证明定理成立。
不妨称式(6)的插值方法为H-边边法。
推论1 当 0→α 时, ][FP 是通常的边- 边方法的插值算子。
证 明注意到式(2)的三次H-Hermite多项式性质,再参考Zhang[14]的方法即可证明。
2.3 边-点插值方法
Nielson[8]在1979 年提出了三角域上的边-点插值方法,也称为径向投影方法,使用3 个插值算子的凸组合来构造三角曲面片,其中每个插值算子满足一个点及其对边上的插值条件。
记iS 为顶点iV 所对应边的点(如图3 所示),则iS 的坐标为
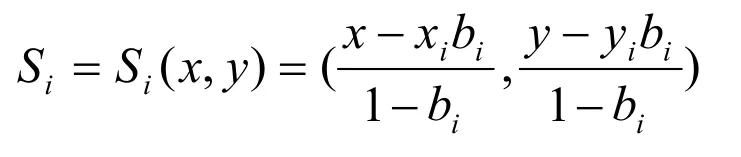
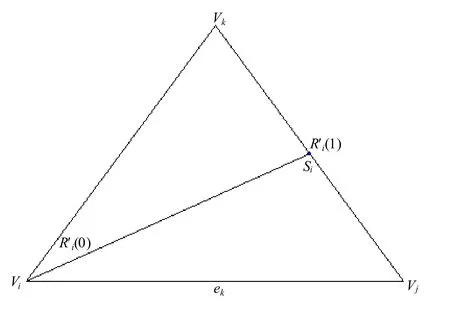
图3 Di[F]插值的几何解释
将Nielson 中基本插值算子 iD 中的广义三次 Hermite 多项式用第二类H-Hermite 多项式替换,有

其中

这里 )(QFx, )(QFy分别表示 ),( yxF 在Q 点的x 方向和y 方向偏导数。
将 D1[F]、 D2[F]、 D3[F]凸组合,定义曲面
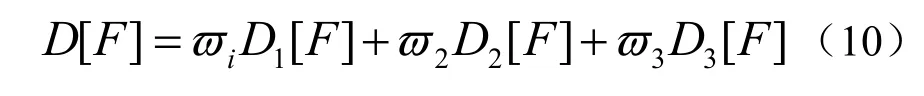
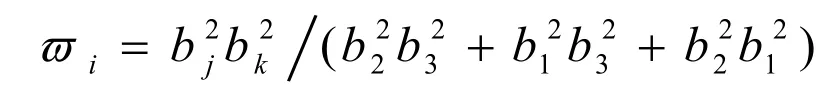
上述的权函数具有性质:
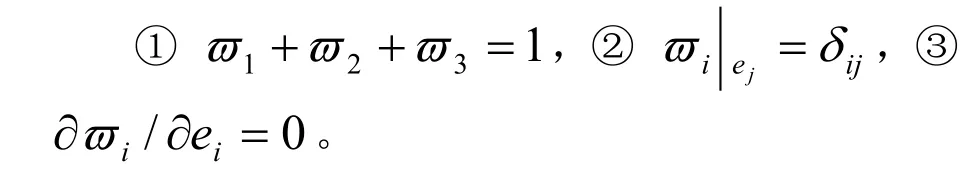
定理2 若 ),( yxF )(1 TC ∂∈ ,则当( x, y)∈∂T 时, D[ F]插值 F ( x,y)及其一阶导矢。
证 明从式(4)知第二类H-Hermite 多项式与Nielson 的边点法的广义Hermite 多项式有相同的性质。即可证明。
不妨称式(10)的插值方法为H-边点法。
推论2 当 0→α 时, ][FD 是通常的边- 点方法的插值算子。
证 明可以按照与Zhang[14]类似的方法证明当 0→α 时,第二类H-Hermite 多项式即为Nielson 的边-点法的广义Hermite 多项式。
3 试验例子
本节通过实际例子,说明前面插值格式的有效性。由于在基本插值算子中,含有分母项,作者选用优秀的符号计算软件Mathematic 绘图。

图4 边-边法插值的曲面
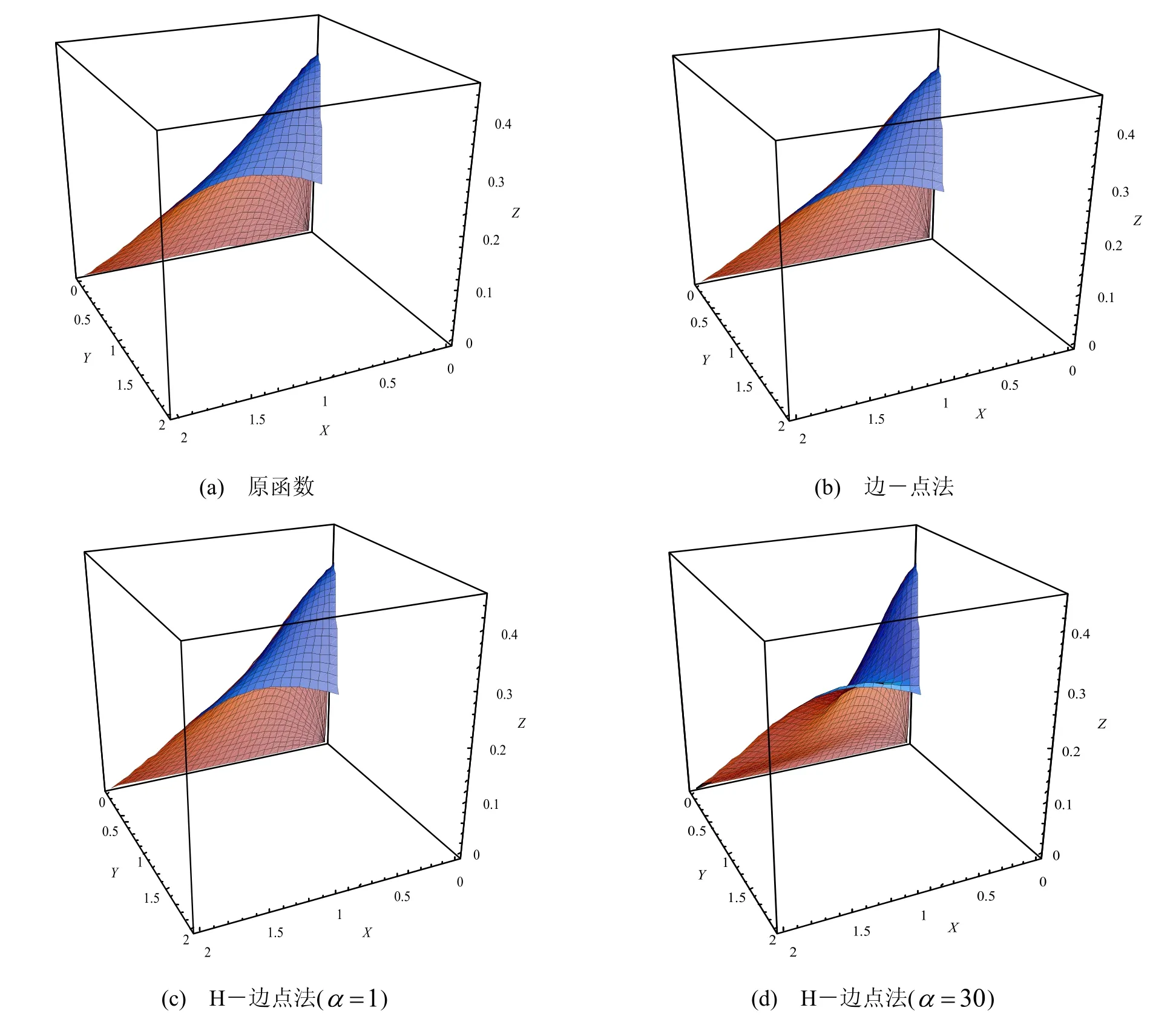
图5 边-点法插值曲面的曲面
从图4、图5 的实际图形可以看出,本文给定的方法都含有形状参数α ,调整形状参数的值可改变曲面的内部形状,而不影响曲面的边界形状。
4 结论及展望
在三角形域上,用两种不同的H-Hermite 多项式代替Hermite 多项式得到了三种C1连续插值边界数据的三角曲面片。构造的三角曲面片均含有形状参数α ,调整α 的值,可改变曲面的内部形状,而不影响曲面的边界形状,当α 0→ 时,可退化为通常的边-边与边-点方法插值的曲面片。最后,实例显示了本文方法的实际效果。
[1] Barnhill R E, Birkhoff G, Gordon WJ. Smooth interpolation in triangles [J]. Journal of Approximation Theory, 1973, 8(2): 114−128.
[2] Barnhill R E, Gregory J A. Compatible smooth interpolation in triangles [J]. Journal of Approximation Theory, 1975, 15: 214−225.
[3] Barnhill R E, Gregory J A. Polynomial interpolation to boundary data on triangles [J]. Mathematics of Computation, 1975, 29: 726−735.
[4] Gregory J A. Smooth interpolation without twist constraints[C]//Barnhill R E, Riesenfeld R F, eds. Computer Aided Geometric Design. New York: Academic Press, 1974: 71−88.
[5] Gregory J A. A blending function interpolant for triangles[C]//Multivariate Approximation. New York: Academic Press, 1978: 279−287.
[6] Gregory J A. C1rectangular and non-rectangular surface patches[C]//Barnhill R E, Boehm W, eds. Surfaces in Computer Aided Geometric Design. Amsterdam: North-Holland, 1983: 25−33.
[7] Barnhill R E, Little F F. Three-and four-dimensional surfaces [J]. Rocky Mountain J Math, 1984, 14: 77−102.
[8] Nielson G M. The side vertex method for interpolation in triangles [J]. J Approx Theory, 1979, 25: 318−336. [9] Hagen H. Geometric surface patches without twist constraints [J]. Computer Aided Geometric Design, 1986, 3(3): 179−184.
[10] Hagen H. Curvature continuous triangular interpolants[C]//Lyche T, Schumaker L, eds. Methods in CAGD. Oslo: Academic Press, 1989: 373−384.
[11] Nielson G M. A transfinite, visually continuous, triangular interpolant[C]//Farin G, ed. Geometric Modeling, Applications and New Trends, SIAM. Philadelphia, 1987: 235−246.
[12] 徐 琳. 三角域上的超限插值方法[J]. 软件学报, 2007, 18(2): 430−441.
[13] Brian A Barsky. local control of bias and tension in beta-splines [J]. Computer Graphics, 1983, 17(3): 193−218.
[14] Zhang Jiwen. C-curves: an extension of cubic curves [J]. Computer Aided Geometric Design, 1996, 13: 199−217.
[15] Wang Guozhao, Yang Qinmin. Planar cubic hybrid hyperbolic polynomial curve and its shape classification [J]. Progress in Natural Science, 2004, 14(1): 41−46.
[16] 胡晴峰, 汪国昭. 双曲混合多项式形式的Ball曲线[J]. 浙江大学学报(理学版), 2004, 31(6): 625−630.
[17] Li Yajuan, Wang Guozhao. Two kinds of B-basis of the algebraic hyperbolic space [J]. Journal of Zhejiang University SCIENCE, 2005, 6A(7): 750−759.
[18] Lu Yonggang, Wang Guozhao, Yang Xunnian. Uniform hyperbolic polynomial B-spline curves [J]. Computer Aided Geometric Design, 2002, 19(6): 379−393.
