稠密采样点模型的快速隐式曲面重建
2010-01-01苗兰芳周廷方彭群生
苗兰芳, 周廷方, 彭群生
(1. 浙江师范大学信息科学与工程学院,浙江 金华 321004; 2. 浙江大学CAD&CG国家重点实验室,浙江 杭州 310027)
现实世界中有许多应用有赖于建立准确的实体模型并进行可视化,如雕像、考古艺术品、大规模地貌以及反求工程中的模型仿制、模具翻新等。由三维扫描仪对模型表面进行扫描,会得到大量的三维采样点,从这些点中重建出逼近于原始实体模型表面的曲面并进行绘制是计算机图形学中一个很重要的研究领域。近年来,随着模型表面复杂度和表面采样点数据的增加,形成了众多大规模采样点数据模型,从这样的数据模型中快速地重建出曲面必然会出现以前小规模数据点模型所没有的问题。
在曲面重建方法中,基于径向基函数[1-3](RBF: Radial Base Function)的曲面重建方法和几何样条曲面的最小二乘拟合[4]是一种基于全局的隐式曲面重建方法,其中RBF 对于不完整的光滑数据模型的修补特别有用,但它有磨光作用,因此很难重建像棱边、尖角之类的明显特征,并且在处理大规模数据点模型的速度很慢。基于Blinn[5]局部隐式曲面加权混合思想之上的曲面重建方法是一种局部的隐式曲面重建方法,如:Muraki等[6]用高斯球的线性组合拟合散乱点云的隐式曲面;Hoppe 等[7]通过估算局部区域内的最近点切平面的有向距离进行隐式曲面重建;Curless 等[8]提出了一种基于对预建的基础表面模型上的距离函数的估算进行隐式曲面重建;Alexa[9]等采用基于投影的形状逼近方法在局部性和直接重采样方面有所突破,但投影需要求解非线性MLS 问题,从而使大部分形状操作非常费时;Ohtake 等[10]对大规模数据点采用多层次剖分MPU 方法,首先对点模型根据其点数和法棱锥角进行八叉树自适应剖分,继而对每个单元重建的局部曲面进行加权混合。
基于局部的隐式曲面重建方法和基于全局的隐式曲面重建方法相比,其最大优势在于:将大规模的数据点云分成小块的数据点云后在小范围内进行隐式曲面重建,然后通过对重建的局部曲面加权混合求得函数值。但该类方法在计算函数值时仍需求解线性或非线性系统方程。Nielson 提出一种基于径向Hermite 基函数的加权对散乱数据点的位置和法向进行插值的曲面重建方法[11]。该方法通过对点附近的最近的模型表面上K 个点的法向和位置信息直接求取函数值,其重建速度快于前面描述的任何一种曲面重建方法,但是该方法不能处理带有噪声的散乱点数据。
针对上述情况,本文提出了一种点模型的隐式曲面的快速重建方法,该方法以局部邻域内采样点的双边滤波函数值为依据,其模型表面附近任意一点的函数值通过该点附近表面上最近的K个采样数据直接估算所得,和以往的曲面重建方法相比,本文方法既不用曲面内、外的支撑点,也不用求解线性或非线性系统方程,具有非常快的重建速度。此外,由于该隐式曲面是基于双边滤波函数之上的,因此,还能对带有噪声的点模型进行特征保持的曲面重建。
1 基于双边滤波函数的隐式曲面重建
双边滤波函数最早被用于图像处理领域的轮廓特征保持的去噪中[12],后来被拓展用于三维数据的网格模型表面去噪,效果相当好[13-14]。尽管这些文献中描述的去噪方法是针对网格模型表面,但同样也适合于点模型表面。
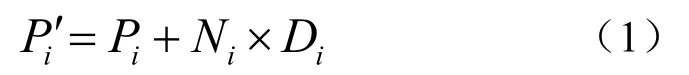
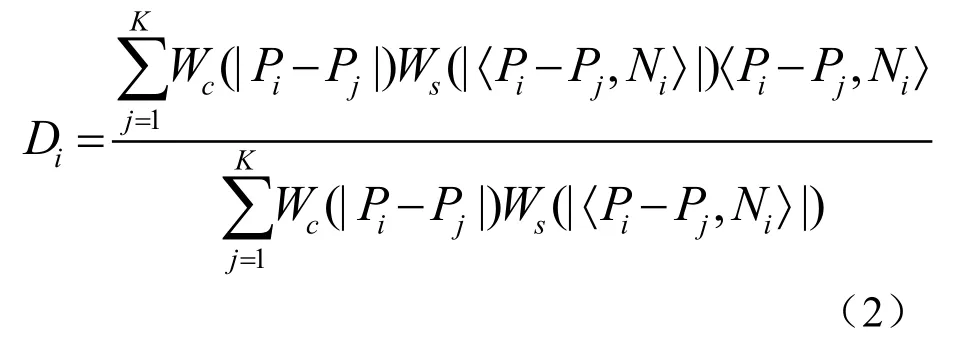
式中 K 为参与函数值计算的离iP 点最近的模型表面上的采样点数,cW 、sW 在图像去噪处理 中,分别作为双边滤波函数的空域和频域高斯滤 波,现分别作为三维模型表面采样点iP 所在的局 部邻域内切平面上和法向高度场的高斯滤波,具体形式如下
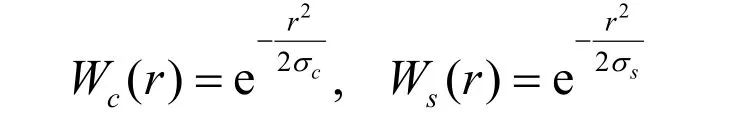
其中sσ 、cσ 分别为其切平面(空域)和法向 高度场(频域)上的高斯滤波系数,它们反映了 计算任意一个采样点P 的双边滤波函数值时的 切向和法向影响范围。采用这个双边滤波函数,可以对模型表面数据进行去噪的同时也能进行特征保持[13-14]。
1.1 任意一点的双边滤波函数值的计算

对于模型表面上任一采样点iP 及其法向Ni,都可得到一个由公式(2)计算所得的双边滤波函数值;而对于模型表面附近任一点P ( x, y , z ),在根据公式(2)计算其双边滤波函数值时,发现还需要先计算该点的法向N ( x, y , z )。
1.2 任意一点的法向计算
Amenta等指出,采样点模型的MLS隐式曲面函数可以表示成二个分量:一个能量场和一个法矢量场[15]。对于采样点模型表面附近任意一点,用MLS表面能量最小法可求出该点的法向。但运用该方法在某些地方会产生不理想的法向(如:距离表面较远的地方和表面附近有明显特征的地方)[16]。为此,他们又提出另外两种表面能量定义方式改进法向场的分布,即:通过邻域采样点加权重心的能量函数以及利用线积分计算的能量函数,但这两种方法都是针对没有法向的采样点模型,而且需求解费时的非线性方程。
对于带有法向的采样点模型,在表面附近任意一点的法向可以估算为与该点最近的模型表面上的K 个点法向的加权和[17],即

式中 K 为距离P 点最近的模型表面的邻域点数, WNi(|P − Pi|)可以为任意一个关于距离|P − Pi|单调递减的正值权函数,如:可以选择Sheperd反距离函数 WNi(| x |) = 1/x及高斯滤波 函数。用这种计算方式估算的模型表面法向场,如图1所示。
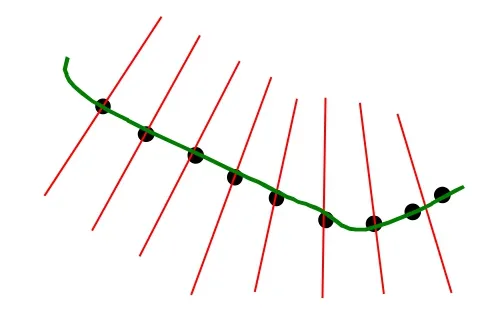
图 1 点模型表面的法向场流线
上述法向估算方法简单、快速,并且可以保证在表面附近的法向场的正确性。但在远离采样点模型表面时,法向场与表面垂直方向会有一定的偏移。在下面将要描述的等值面抽取算法中,由于只是利用了采样点模型表面附近的函数值及其相应的法向场,因此,可以保证重建曲面的正确性。
1.3 采用双边滤波函数进行隐式曲面重建
由公式(2)计算的双向滤波函数值D,在采样点模型表面附近构造了一个距离场,该距离场可以采用某种等值面抽取方法(如:移动立方体方法MC:Moving Cube)抽取出任意函数值的等值面,其中距离值为零的等值面即为点模型表面。图2是分别利用MC等值面抽取方法对兔子点模型表面附近函数值为零、+0.2和-0.1的等值面进行抽取的结果。在用MC方法对等值面进行抽取时,被剖分的移动小立方体已足够小,所抽取的等值面与模型表面的距离最大也不会超过小立方体的对角线,这一点为采样点模型隐式曲面的正确重建提供了保证。

图 2 采用本文方法重建的Bunny模型结果(图中绘制模型在显示时作了一定比例的缩放)
2 基于双边滤波函数的隐式曲面重建的应用
由于双边滤波函数的去噪保特征的性质,因此,利用双边波滤函数进行隐式曲面重建时,对带有一定噪声和失真的采样点模型能进行去噪保特征的隐式曲面重建,此外,基于双边滤波函数的隐式曲面重建方法还可以方便地进行实体几何造型。
2.1 去噪和特征保持
去噪采用Nielson方法重建不含噪声的稠密采样点模型时,一般不会遇到问题,这是因为Nielson方法是直接对点的位置和法向的插值进行隐式曲面重建的[11],但该方法应用于带有噪声的稠密采样点数据模型时,就会得到很不理想的结果,如图3(b)所示。本文提出基于双边滤波函数对稠密采样点数据模型进行隐式曲面重建的方法,具有比较好的重建效果。如图3(c)所示。无论是用Nielson的方法,还是用本文提出的方法,当得到的模型表面的采样点数据比较稠密且又比较准确时,都会得到相当好的结果,如图4所示,尽管仍可从图中看出某些细微的差别,如:采用后者的方法所重建的模型表面(如图4(b))光滑于采用前者方法所重建的模型表面(如图
4(a))。

图 3 带有噪声的Bunny数据模型的表面重建结果

图 4 无噪声的稠密采样点模型的隐式曲面重建结果
显著特征的保持虽然基于双边滤波函数的隐式曲面重建能对采样点模型进行特征保持的表面重建,但对于比较明显的模型表面特征(如CAD模型的边、角等),如果只用上述重建方法,则会不同程度地削弱边角特征的锐度。对此,在计算函数值时,首先对搜索到的模型表面上最近的K个采样点进行关于其法向的分类(具体方法可参看MPU有关明显特征重建方法[10]),如图5所示,然后,取最近的一类点计算函数值;更精确一点的方法还可以先把这些点按其特征所对应的法向分成几簇,再采用布尔交运算求交的方法。

图 5 采样点模型附近任意一点P的最近采样点 邻域的明显特征示意图
2.2 布尔操作
为了下面描述方便,将FA记为与采样点集A相对应的体模型或距离场函数,A的外侧可表示为
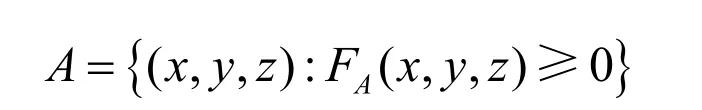
本文的距离场函数是采样点模型表面的双边滤波函数,而其外表面隐式地逼近于由其采样点集所定义的表面。设B是另一个三维采样点模型,其所对应的体模型或距离场函数为FB,其外侧为

则很容易定义上述两个模型的并

相应地距离场函数的并定义为
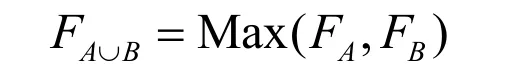
同样的,可定义两距离场函数的交和差为
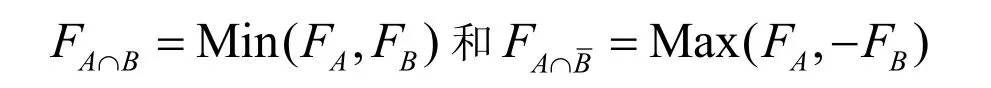
甚至还可以定义一些混合(Blend)距离场函数,如双曲线混合
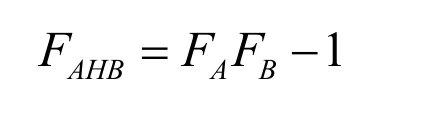
3 实验结果及分析
本文所有实验结果均采用MC方法进行隐式曲面三角化。在绘制时,发现MC方法在不同精度的小立方体下对采样点模型细节有着不同程度的保留效果。图6是对于右半边数据不完整模型Venus头像的重建结果,其中图6(a)原始数据模型,图6(b)、图(c)、图(d)为不同小立方体边长(分别为:0.7,0.5,0.3)下的重建结果,图6(b)的点数为28582,比原始模型的点数(72545)少了几倍,这意味着其分辨率比原始模型降低了几倍,因此在其绘制结果中丢失了好多细节;图6(c)的点数为87536,该点数略多于原始模型的点数,其重建结果图像保留了细节,但由于原始模型中左一半采样稠密,而右一半采样较稀,因此,重建后左边的实际分辨率还是低于原始模型;图6(d)的点数为155708,自然分辨率已高出原始点模型一倍,但绘制结果相对于图6(c)没有特别明显的改进。因此,在用移动立方体方法进行模型的等值面抽取时,对小立方体的边长应进行自适应的调整。这样,既能避免不必要的冗余,又能避免细节丢失。

图 6 不完整数据模型Venus(72545)在不同小立方体边长下重建的结果(括号内为点数)
图7显示了对Buuny模型(点数为35283)取不同分辨率并施加不同次数的双边滤波函数进行重建的结果。左图为对原始点模型使用一次双边滤波函数后重建的结果,中图和右图分别为对左图结果(即:顶点及其法向)施加双边滤波函数一次、二次进行重建的结果;上、下二排的小立方体边长分别为:0.007和0.003;点数分别为:27114、26916、26726;148130、144312、145728。可以看出,其一,分辨率越高,重建的细节越明显;其二,增加使用双边滤波函数进行重建的次数,可以使分辨率低的模型表面趋向于光滑,而对于分辨率较高的模型的影响甚少。

图7 对Buuny 模型(点数为35283)在不同小立方体边长(上: 0.007,下: 0.003)时施加1 次(左),2 次(中) 和3 次(右)的双边滤波函数进行重建的结果(上排逐渐光滑,下排光滑很少。图中右下角为点数)
图8从左到右分别为点模型venus采用不同小立方体边长的MC算法进行连续六次等值面抽取的结果。小立方体边长越大,其细节磨损程度越大,其重建模型表面也就越光滑。而在与图7中相对应的重建结果比较中,可以看出,在分辨率较高(小立方体边长较小)的重建中,其细节随着重建次数的增加,其磨光程度较低,但相对于原始模型,还是变得光滑了。

图8 从左到右图分别为点模型venus 采用不同小立方体边长的MC 算法进行连续六次等值面抽取的 结果(小立方体边长越大,其细节磨损程度越大,重建模型表面就越光滑)
图9所示为采用本文提出的基于双边滤波函数进行隐式曲面重建的方法对采样点模型进行布尔运算的结果。图中所用模型的点数分别为:兔子10k,圆环32k,vase68k,venus50k,球10k以及dinosaur56k。由此结果可知,采用双边滤波函数进行隐式曲面重建可以很容易很鲁棒地实现实体几何造型中的布尔运算。

图 9 基于双向滤波函数的隐式曲面的布尔运算
4 小 结
本文提出了一种基于双边滤波函数的隐式曲面重建方法。在计算函数值时,只需将模型表面上最近的K个点的位置和法向信息代入公式(2)进行直接计算,无须求解线性或非线性系统方程,与采用RBF、MLS及MPU的重建方法相比,新方法在时间上的优势是最为明显的;此外,该方法还能对带有噪声的数据模型进行表面重建,且具有很好的去噪保特征的重建效果。实验结果表明,基于双边滤波器的隐式曲面是一种非常有效的曲面表达形式。
[1] Carr J C, Beatson R K, Cherrie J B, et al. Reconstruction and representation of 3D objects with radial basis functions [C]//Proceedings of ACMSIGGRAPH 2001, 2001: 67-76.
[2] Turk G, O’Brien J. Modelling with implicit surfaces that interpolate [J]. ACM Transactions on Graphics, 2002, 21(4): 855-873.
[3] Ohtake Y, Belyaev A G, Seidel H P. A multi-scale approach to 3D scattered data interpolation with compactly supported basis functions [C]//Shape Modeling International 2003, 2003: 153-161.
[4] Jüttler B, Felis A. Least-squares fitting of algebraic spline surfaces [J]. Advances in Computational Mathematics, 2002, 17: 135-152.
[5] Blinn J F. A generalization of algebraic surface drawing [J]. ACM Transactions on Graphics, 1982, 1(3): 235-256.
[6] Muraki S. Volumetric shape description of range data using “Blobby Model” [C]//Proceedings of ACMSIGGRAPH 1991. Computer Graphics, 1991: 227-235.
[7] Hoppe H, DeRose T, Duchamp T. Surface reconstruction from unorganized points [C]// Proceeding of Siggraph 1992, 1992: 71-78.
[8] Curless B, Levoy M. A volumetric method for building complex models from range images [C]// Proceedings of SIGGRAPH 1996, 1996: 303-312.
[9] Alexa M, Behr J, Cohen-Or D, et al. Point set surfaces [C]//IEEE Visualization 2001, 2001: 21-28.
[10] Ohtake Y, Belyaev A, Alexa M, et al. Multi-level partition of unity implicits [C]//Siggraph 2003 Proceeding, San Diego, 2003: 463-470.
[11] Nielson G M. Radial hermite operators for scattered point cloud data with normal vectors and applications to implicitizing polygon mesh surfaces for generalized CSG operations and smoothing [C]//IEEE Visualization 2004, 2004: 203-210.
[12] Smith S M, Brady J M. SUSAN: a new approach to low level image processing [R]. Technical Report, 1995.
[13] Fleishman S, Drori I, Cohen-Or D. Bilateral mesh denoising [J]. ACM Trans. Graph, 2003, 22(3): 950-953.
[14] Jones T, Durand F, Desbrun M. Non-iterative, feature preserving mesh smoothing [J]. ACM Trans. Graph, 2003, 22(3): 943–949.
[15] Amenta N, Kil Y J. Defining point-set surfaces [J]. ACM Trans. Graph, 2004, 23(3): 264-270.
[16] Amenta N, Kil Y J. The domain of a point set surface [C]//Proc. of Eurographics Symposium on Point-Based Graphics 2004, 2004: 139-147.
[17] Alexa M, Adamson A. On normals and projection operators for surfaces defined by point sets [C]//Proc. of Symp. on Point-Based Graphics 2004, 2004: 149-155.
