利用Bandelets 变换的电子探针图像 融合优化算法研究

李 祥 ， 何剑锋， 刘凤玉

（1. 南京理工大学计算机系，江苏 南京 210094； 2. 东华理工大学核资源与环境教育部重点实验室，江西 南昌 330013）

现代科学技术的迅速发展，要求材料科学工作者能够及时提供具有良好力学性能的结构材料及具有各种物理化学性能的功能材料。而材料的性能往往取决于它的微观结构及成分分布。因此，为了研究新的材料或改善传统材料，必须以尽可能高的分辨能力观测和分析材料在制备、加工及使用条件下（包括相变过程中，外加应力及各种环境因素作用下等）微观结构和微区成分的变化，并进而揭示材料成分―工艺―微观结构―性能之间关系的规律，建立和发展材料科学的基本理论[1]。电子探针 X 射线显微分析是目 前比较理想的一种微区成分分析手段。电子探针仪[2]利用高能电子与固体物质相互作用的原理，通过能量足够高的一束细聚焦电子束轰击样品表面，在一个有限的深度和侧向扩展的微区体积内，激发产生特征X 射线信号，它们的波长（或能量）和强度是表征该微区内所含元素及其浓度的重要信息，采用适当的谱仪和检测、计数系统可达到成分分析的目的。利用电子探针进行样品检测时，可获得二次电子、反向散射等多种类型的微表面影像。每一种图像都包含了丰富的形态和空间结构信息，是样品表面形态分析的重要手段之一。然而，电子探针仪器本身没有提供多图像的复合处理机制，必须依靠使用人员靠经验和主观目测的方法来综合分析不同类型图片，以得到综合的表面形态分析结果，李镜明[3]等人用小波技术对电子探针影像复合处理作过初步探讨。

近年来，图像融合是近几年来飞速发展的一门技术，是多源信息融合的重要分支。是指将两个或两个以上的传感器在同一时间或不同时间获取的关于某个具体场景的图像或图像序列信息加入综合，以生成新的有关此场景解释的信息处理过程[4]。由于融合图像能提供比任何单一图像更加丰富而精确的信息，因此在遥感图像、医学图像、计算机视觉等众多领域得到广泛应用。而基于多尺度分解的小波图像融合方法更是当前技术发展主流，而结合人眼视觉特性的各类超小波图像融合方法更是呈现百花齐放的态势。由Pennec 和Mallat 提出的Bandelet 变换更提供了一种新的基于边缘的图像表示方法，能自适应地跟踪图像的几何正则方向，具有最大限度保留图像细节的优良特性[5]。本文结合电子探针所获得的微区影像多样性特点，利用Bandelet 变换在图像几何结构描述方面的优越性，提出先利用Bandelet 变换的方法对样品二次电子图象、反向散射电子图象和样品电流图象进行基于二代Bandelet 的图像分解，然后再根据高频系数和低频系数的特点，低频部分采用能量平均值方法进行综合，而对高频系数部分则采用相似度拟合的融合规则进行融合处理，最后将融合信息重构获得高信息量的EPMA 融合图像。

1 EPMA 图像特性

在电子探针分析中，经过加束聚焦的高速电子束入射到电样品时，入射电子便与试样原子核外电子发生相互作用，经历一系列的弹性散射和非弹性散射过程，其中某些电子发生大角度散射或多次小角度散射，当总的散射角超过90°时，这些电子就有可能重新通过入射表面而被反射出来，这样反射出来的电子叫背散射电子。通常背散射电子的数目随样品的原子序数的增加而增加，因此在相同的条件下，不同物质因为产生背散射电子数目的多少不一样，因此利用检测背散射电子的探测器，可以定性的区分不同的物质。当然除此之处，背散射电子还与电子束的入射角度和样品表面形貌有关，所以除了成份信息外，背散射电子还能提供样品表面的形貌信息。

Kimoto 和Hashimoto（1969）设计了一种将成分信息和形貌信息分开来的方法。他们将两个电子探测器对称的配置在入射电子束的两边，使得进入左右两个探测器的原子序数信息，其数值大小和极性都相同，而对于表面形貌信息，则数值大小相同，极性相反。因此，用电子光学的方法将两个探测器所得到的信息相加，便得到了样品成分（平均原子序数）信息，通过计算机扫描成像处理，即得到了COMP 图像(背散射电子像），能反映样品的成分和形态等信息；TOPO图像则是将两信号相减，再通过计算机扫描成像处理所获得的图像，它能反映样品的空间形貌信息，但分辨率没有SEI 高。二次电子图像（SEI）则是二次电子是从试样表面反射回来的电子能量低于50eV 的电子。如果核外电子所获得的能量大于其电离能，则该电子可能为自由电子，如果这些电自由电子很靠近样品表面时而且能量大于相应的逸出功，则可能从样品表面逸出而成为二次电子。由于二次电子能量低，只有表面100埃以内的二次电子才有可能逸出而被检测到，因此能反映出样品形态特性，具有很高的空间分辨率（见图1）。

图1 同一样品的背散射电子影像（COMP）、二次电子影像（SEI）和TOPO 图像（已进行位置配准）

2 Bandelet 变换分析

图像是一种特殊但常见的二维信号f (x1, x2),自然界中的图像可以看做是由光滑区、纹理区和几何形状区的组合体[6]。研究表明，人眼对不同区域内的图像信息的敏感程度存在差异性，主要包括对图像边缘信息、图像平滑区信息及纹理区信息的失真不太敏感造成的。在图像处理中，传统的解决方法是用二维离散小波进行处理，这种小波对于图像中的点状奇异性、光滑区域和纹理区都能做到有效地表示。但是，二维离散小波只是在水平和垂直两个角度进行图像分析，并且在每个方向进行滤波及采样计算时都是等同的，而实现图像一般是任意方向的，这样必然具有各向同性和方向性缺失。

Bandelet 变换是Pennec 和Mallat[5,7-8]自2000年起在多篇论文中提出的一种新型自适应多尺度几何图像分析工具，它的核心思想是把图像中的几何特征定义为矢量场，而不是简单地看成是普通边缘的集合，以便自适应跟踪图像内在的几何结构，捕获其所含的几何正则性，从而给出最优化的表示。

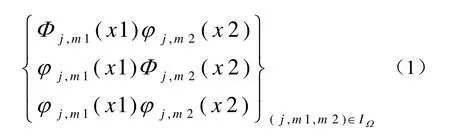
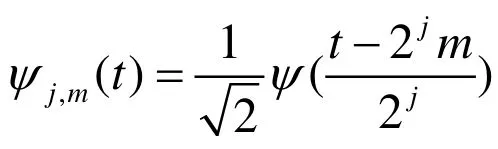
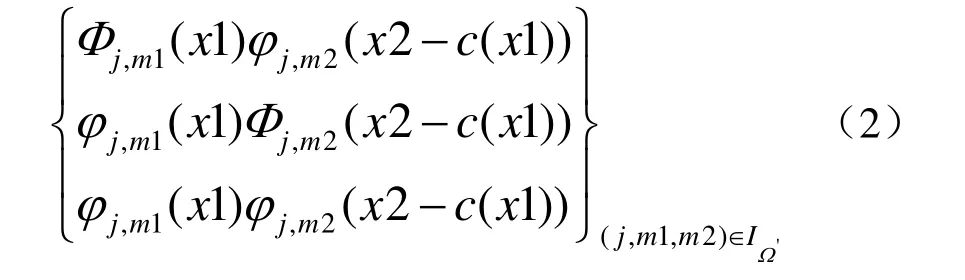
然后再借助于可分离小波基来进行处理。实现过程中的弯曲作用如图2 所示。

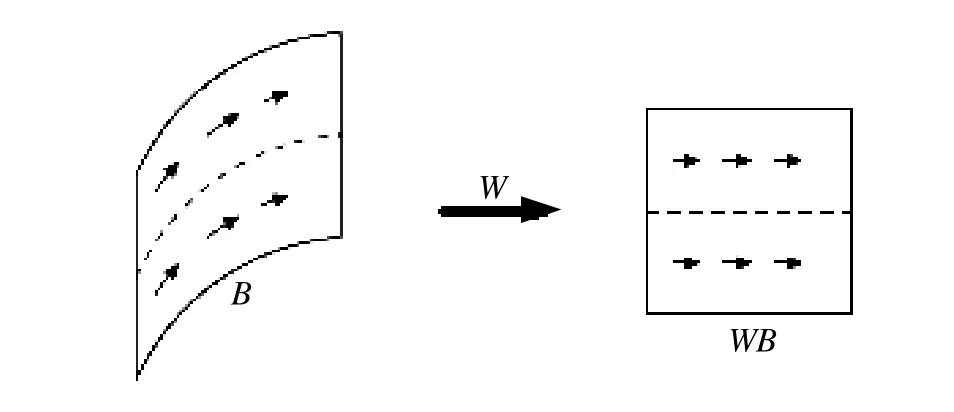
图2 水平型区域B 和相应的变换区域WB

3 二代Bandelets 变换的融合

基本Bandelet变换能实现有效的图像稀疏矩阵表示，但分解过程需量大量的重采样和弯曲等操作，算法实现太复杂，时间效率低。G.Peryre和Mallat 在2005 年提出了改进的Bandelet 变换，也称为第二代Bandelet 变换[9]，通过多尺度分析和几何方向分析共同完成图像的分解，从而提高分解的运算速度。

基于二代Bandelets 变换的图像融合的一般流程包括以下步骤[10-11]：

第1 步 对图像进行二维离散小波变换，获得高频部分和低频部分图像；

第2 步 对于低频尺度系统的融合，一般直接采用平均法融合即可；

第3 步 对于高频细节部分子图像，先对图 像进行4*4 区域划分，得到 iΩ ；

第4 步 在每个区域中，重采样图像的样值，计算出每个区域的几何流 Gj(i)及其相应的Bandelet 系数Cj(x, y, i)，其中j 代表是那一个图像，i 表示在图像的那一个区域，(x, y)表示这一像素点的位置。

第5 步 融合规则的选择。对于同一样本的不同EPMA 图像，局部图像内容有可能是不同的。因此，EPMA 图像融合，实际上是一种图像互补性融合。因此，在选择融合规则时，应尽可能的兼顾各个图像的内容，以免再次丢失部分源图像中的信息。对于几何流Gj(i)，采取最大值融合规则

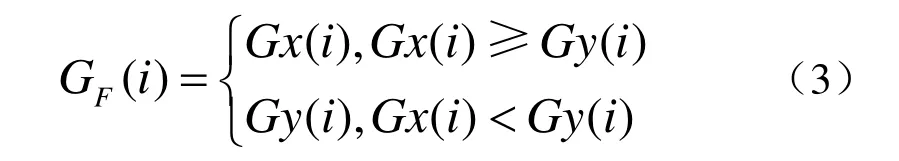
而对Bandelet 系数Cj(x, y, i)，则采用基于区域矩形特性选择加权平均法进行，统计每个对应子块的方差，确定图像X 和Y 每个子块的加权系数K1, K2，如X 图像方差大于Y 图像方差，则K1>=K2，否则K2>=K1，得到每个子块图像的融合数据为

以最大限度地保留各源图像的信息。

4 融合仿真与效果评测

为检验二代Bandelet 变换的影像融合效果，本文采用了严格配准的2组EPMA图像在Matlab平台进行了融合仿真实验。对第1 组BSE 和TOPO 样品图像数据，直接进行融合处理；而于对第2 组BSE、TOPO 和SEI 样品影像数据，则采用两两分级融合的方法，先让前两个图像进行融合，然后把融合的结果和第三幅图像进行融合，得到最终的融合图像。对低频采用基于平均值的融合规则，高频系数中的几何流采用最大值融合规则，对于Bandelet 系数融合则采用区域加权方差规则，区域大小为4×4。实验结果如图3所示。

对于图像融合效果的评价可以通过主观评价法和客观评价法进行。主观评价法是由判读人员通过眼睛观看直接对图像的质量进行评估。其主要用于判断融合图像是否配准，如果配准不好，那么图像就会出现重影；判断色彩是否一致；判断融合图像整体亮度、色彩反差是否合适，是否有蒙雾或马赛克现象；判断融合图像的清晰度是否降低，图像边缘是否清楚；判断融合图像纹理及色彩信息是否丰富，光谱与空间信息是否丢失等。当融合图像之间差异比较明显时，主观评价方法可以快速地得出准确的评判结果。实验显示，融合图像从视觉判断来说，都能较全面的包括各来源的图像内容信息，边缘和纹理都很清楚。

客观评价法是针对融合图像提出的一系列质量指标，以及对融合方法提出的量化评价公式，由计算机根据量化评价公式计算融合图像的质量指标，并根据质量指标的统计结果对融合方法进行评价。量化评价可以提高判断的准确性和速度，同时采用多种量化判据可以弥补各自方法上的缺陷，得到更正确的结论。为了对算法的融合性能进行量化比较，本文采用信息熵、标准差、平均梯度，作为客观衡量标准，表1 显示上述图像的信息熵、标准差、平均梯度的客观评价结果，从表中可看出，基于区域Bandelet变换的信息熵，标准差、平均梯度都要比源图的值高，由此说明基于区域Bandelet 变换的融合方法的优越性。

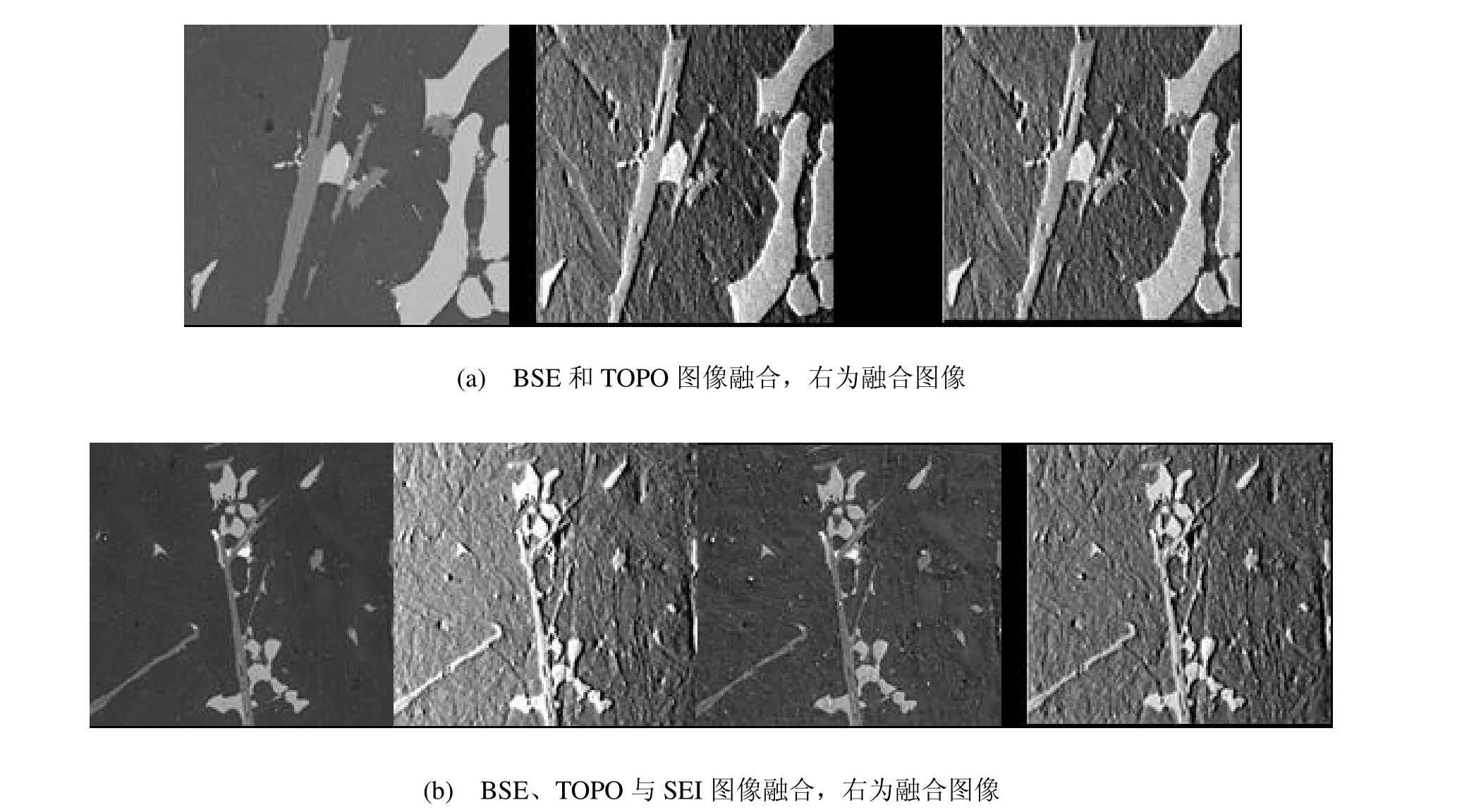
图3 EPMA 图像 Matlab 融合实验结果

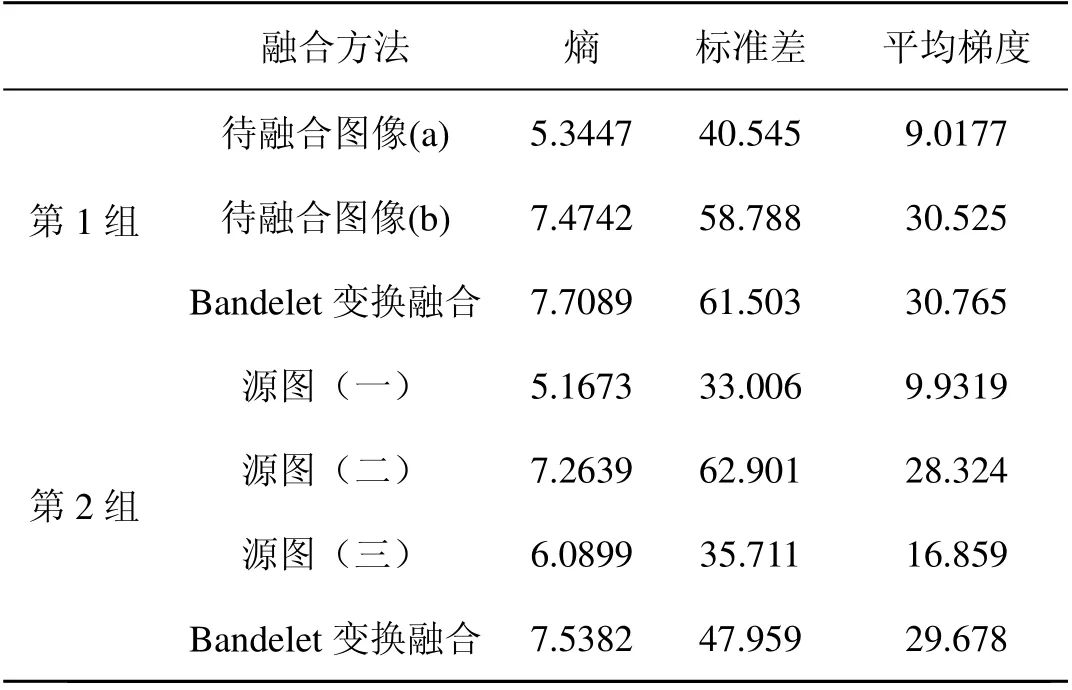
表1 EPMA 图像融合的客观评价

5 结 束 语

电子探针图像复合处理方法的引入，进一步扩展了样品微表面检测中EPMA 图像处理领域，是对样品测试过程中图像处理的优化应用，对提高样品图像在检测中的实用价值，以及为进行微表面影像的三维重构奠定了良好的基础。

当然，本文仿真实验是利用Bandelet 变换进行基于静态样品图片的处理，而对于动态图像序列的融合处理，更要考虑到图像帧内关系与帧间关系，还有帧信号数据的丢失恢复等，还是其它超小波在图像融合中的特殊属性，都是希望进一步深入研究的内容。

[1] 晋 勇, 赵海波, 等. 现代分析技术在薄膜材料研究中的应用[J]. 工具技术, 2003, 37(10): 12-16.

[2] 李德忍. 电子探针微区分析[EB/OL]. http://www. chinabaike.com/article/baike/1000/2008/20080511145 2529.html

[3] 李敬明, 陶德元, 郝 莹. 小波变换在扫描电镜图像处理中的应用研究[J]. 电子显微学报, 2003, 22(1): 75-77.

[4] 覃 征, 鲍夏民, 李爱国. 数字图像融合[M]. 西安:西安交通大学出版社, 2004. 1-5.

[5] Gabriel Peyré, Stéphane Mallat. Orthogonal bandlet bases for geometric images approximation [J]. Communications on Pure and Applied Mathematics, 2008, 61(9): 1173-1212.

[6] 焦李成, 侯 彪, 王 爽, 等. 图像多尺度几何分析 理论与应用[M]. 西安: 西安电子科技大学出版社, 2008. 397-454.

[7] Pennec E Le, Mallat S. Sparse geometrical image representation with bandelets [J]. IEEE Trans. on Image Processing, 2005, 14(4): 423-438.

[8] Erwan Le Pannec, Stephane Mallat. Bandelet image approximation and compression [J]. SIAM Journ. of Multiscale Modeling and Simulation, 2005, 4(3): 992-1039.

[9] 阎敬文, 屈小波. 超小波分析与应用[M]. 北京: 国防工业出版社, 2008. 111-143.

[10] Qu Xiaobo, Yan Jingwen. A novel image fusion algorithm based on bandelet transform [J]. Chinese Optics Letters, 2007, 5(10): 569-572.

[11] Yang Bin, LI Shutao. Multi-focus image fusion using watershed region segmentation and morphological wavelet transform [C]//Proceeding of the International Collequium on Information Fusion, 2007: 317-321.