采用边界拉伸的干涉检验方法与装配顺序规划

魏 锋， 段 鹏， 巩 琦

（河南理工大学机械学院，河南 焦作 454003）

干涉检验[1]是虚拟装配中的重要研究内容和关键技术。当前，该领域的热点问题是如何提高干涉检验精度，提高算法效率。

现有的虚拟装配系统多依托于商业CAD 系统，其静止干涉检验采用CAD 系统的API 程序即可实现，相对简单。对于运动干涉检验，没有特定API 函数，需要开发人员自行设计方案及程序来完成，相对较复杂。常用的动态干涉把装配件的运动轨迹离散化[2-9]，按照装配路径方向将装配件依次放置于装配路径的若干离散点，在离散点处检验装配件与外界环境（如固定件、夹具）的干涉情况。该算法的关键问题是离散点之间的距离设定问题，即运动步长选取。若步长过长，干涉检验精度较差；步长过短则计算量大，影响检查速度。为解决上述矛盾，提出一种基于边界拉伸的干涉检验方法，此方法改变了传统动态干涉检验思想，将原本离散问题转化为连续问题，既可提高干涉检验精度，又降低了干涉检验的计算量。

装配顺序的确定是装配工艺规划的核心。装配顺序是描述产品装配过程的一个重要信息，装配顺序规划自动化对于实现装配顺序优化和缩短装配顺序规划时间具有重要意义。干涉检验与装配顺序是息息相关的，利用干涉检验的结果使装配顺序生成算法既有完备性又有高效率。

1 基于投影边界拉伸方法的干涉检 验

常用的移动方法是设定步长后，通过变幻矩阵移动零件，每次移动后进行检验。将零件轮廓的轨迹包络后，相当于零件轮廓的拉伸体，可用拉伸来进行检验，如图1 所示。精确算法中，可在零件的极限面上获取零件三维图形的二维投影的精确轮廓线，然后进行拉伸。但在可行性运算中，局部自由度和全局自由度结合，不用十分精确的定量计算。定量计算需要获取精确的轮廓线，涉及图形学的算法，相对较复杂。在定性计算中，只要获取零件的包容盒，利用极限点在面上投影，拉伸后形成新的图形，就可进行干涉检验了。

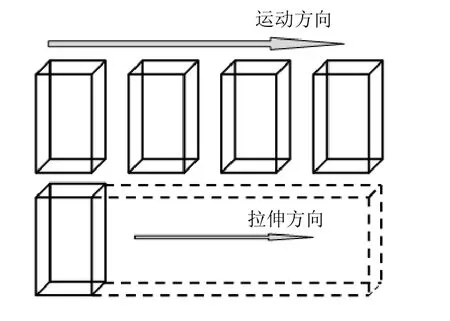
图1 零件的轮廓运动轨迹与拉伸比较

1.1 包容盒获取

包容盒就是在部件坐标系内，能够包容部件所有几何特征的长方体，该长方体的各面与坐标系的坐标平面平行或者垂直。在CAD 的二次开发软件中，都有获取包容盒的函数，如果没有，可以直接获取坐标系的极值点，从而形成一个包容盒（见图2）。

图2 零件的包容盒

1.2 极限面投影

获取极限点后，建立在某一方向的极限面，如+x 方向的最大点，如图3，A 即为+x 方向上的极限平面，建立平面后，设Y 轴的极大值为+y,极小值为-y，Z 轴的极大值为+z，极小值为-z，用（+y, +z），(+y, -z)，(-y, -z)，(-y, +z)建立矩形。分别在需要考察的方向，建立平面，投影，为拉伸做准备。

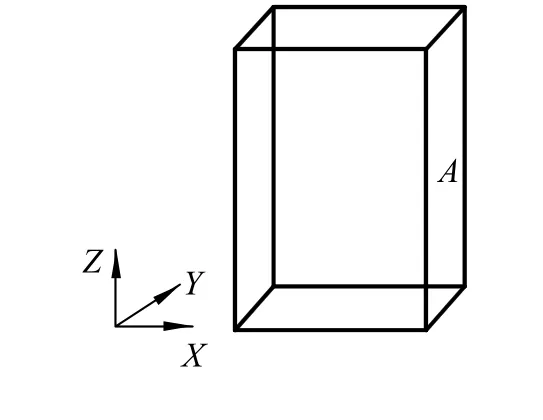
图3 零件的极限面

1.3 基于拉伸的干涉检验

依次对各个方向和每个零件进行基于拉伸的干涉检验，形成零件全局干涉表，如在某一方向上没有与之干涉的零件，则记为空。

步骤1 把原件抑制后，拉伸极限面上的投影轮廓；

步骤2 拉伸的件与其他零件在某一方向上进行干涉检验；

步骤3 把与之干涉的零件放入表格；

步骤4 删除拉伸件，把原件抑制解除。

1.4 干涉剔除

在轴中心约束的时候，由于包容盒的选取，会在本没有干涉的地方造成干涉，所以应在孔轴方向上设置优先方向，则不仅可以解决干涉剔除问题，还可以在一个方向上装入尽可能多的零件，这样可以简化夹具，最小化装配费用。因此，确定优先拆卸方向具有重要的意义。通过前面的约束查询，可以知道在某一方向的轴向约束都有哪些零件，放入优先拆卸的集合。零件应尽可能在优先方向上进行装配。如果有几个优先方向，根据工程实际，采取以下规则：设有N 个优先方向，若每个优先方向能够拆卸的零件数分别为Mi(i =1, 2, …, N )，则

（1） 每次选取能够拆卸的零件数为最大的方向；

（2） 拆卸零件后，优先方向数N 减1；

（3） 重复（1）、（2）步骤直到N =0。

2 基于干涉检验方法的装配顺序规划

2.1 基于干涉检验的装配顺序规划原理

Gottipolu[10]提出了一种装配顺序推理方法，其推理方法可简单描述如下：

首先定义两个向量：接触向量C ={C1, C2, C3, C4, C5, C6}和干涉向量T={T1, T2, T3, T4, T5, T6}，其次定义6个方向：+X , +Y , +Z, -X , -Y 和-Z。

该装配顺序的分析推理过程为：

步骤1 将装配体划分为若干割集；

步骤2 针对每个装配割集，利用装配体的几何设计信息，求出零件及子装配体之间的接触向量和干涉向量；

步骤3 利用接触向量计算出零件之间是否具有装配连接关系，即装配的可能性。

把大的装配零件分为部件，接触向量和干涉向量用零件局部配合约束表和零件干涉表来表示。根据此法则，需要从装配模型中提取出生成装配顺序所需要的信息。局部自由的零件可以移动无限小距离而不与其它零件产生干涉，全局自由的零件可以移动无限远距离而不与其它零件产生干涉。从配合约束可以得到每个零件的局部自由度，即接触向量，还可推理出装配几何优先关系。提出基于轮廓拉伸的方法，可获得全局干涉变量，即上面所说的干涉变量。

在利用拆卸法求装配序列时，通过分析零件局部配合约束表，可以从待拆卸的零件中得到下一个候选拆卸零件，然后再求其全局自由度即干涉向量去测试可行性。零件的局部自由度放入零件局部配合约束表中。通过两个表格就可获得装配顺序，零件局部配合约束获取方法如下：如图4所示，为简化起见，在装配顺序规划中，可以把配合约束简化为3种基本配合形式：面配对，面对齐，中心对齐。实际上，面配对和面对齐在本质上是相同的，适用于平面的配合。前者两配合面的法矢反向，而后者两配合面的法矢同向，可用来提取局部自由度。中心对齐适用于圆柱面的配合，即孔轴配合是圆柱面的中心线的共线配合，作为优先方向。通过装配时的约束条件可以改为上述3种约束方式，分为6个方向[11]。

图4 零件约束示意图

2.2 基于零件干涉表的装配顺序规划算法

根据拉伸干涉检验可得到零件的干涉表；根据装配体的配合关系求出各零件的局部约束表以及优先拆卸方向集；根据优先拆卸方向集求出可拆卸零件集，并得到最优方向的选择次序。例如，装配体由4个零件组成，分别用数字1～4表示。

2.2.1 创建零件干涉表

零件全局干涉表表示零件沿某一方向移动到无穷远的过程中与其干涉的零件。前面已用拉伸算法解决。制成如表1所示，通过干涉检验，把结果填入4个零件在6个方向上与之干涉的零件即可。作为全局干涉表（空的地方为#）。

表 1 零件干涉表

2.2.2 零件的局部配合约束表

零件的局部配合约束表是指根据零件的配合关系而获得的相配合零件的干涉表。例如，装配体由4个零件组成，分别用数字1～4表示。把通过三种装配关系获得的结构填入如表2所示，作为局部干涉表。

表 2 局部配合约束表

2.2.3 基于干涉表的装配顺序规划算法

第一步产生动态干涉表，其初值与零件干涉表相同；产生动态配合约束表，其初值与局部配合约束相同；

第二步从优先拆卸方向集中取一优先方向；

第三步搜索动态配合约束表，若存在零件满足其在动态配合约束表的值和在动态干涉表的值均为“ # ”，就将此零件放入该优先方向的拆卸零件集中；然后更新动态配合约束表和动态干涉表，重复第二步；若不满足，则换取优先拆卸方向集中下一个优先方向，动态干涉表赋初值，动态配合约束表赋初值，重复第二步，直到所有的方向取完；

第四步根据两个表格继续确定装配顺序，直到所有表格都为#。

3 应用实例

此方法已用于换热器的虚拟装配中。程序通过从零件库中提取零件，通过程序进行自动装配，装配完成后如图5 第一幅小图所示，获取各个零件的包容盒，如第二幅小图所示。分别按照 6 个方向对零件拉伸，并进行检验，最后把结果放入数据库的两个表格中。通过两个表格，对装配顺序重新调整。

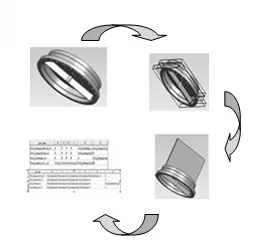
图5 换热器实例

4 结 束 语

通过拉伸的方法，减少了运算量，提高了效率。选择的方法以投影的轮廓为包容盒，为了达到更精确的程度，可把包容盒转化为轮廓线。在以后的研究中，应建立零件优先顺序的知识库，通过程序查询得出结果。

[1] Jimenez P, Thomas F. 3D collision detection： a survey [J]. Computers & Graphics, 2001, 25(2)： 269-285.

[2] Ganter M A, Isarankura B P. Dynamic collision detection using space partitioning [J]. Journal of Mechanical Design, Transactions of the ASME, 1993, 115 (1)： 150-155.

[3] 张 宇, 马丽红, 余英林. 空间模型碰撞检测的向量符号分析与实现[J]. 中国图像图形学报, 1998, 3(6)： 481-484.

[4] 王兆其, 赵沁平. 一个计算凸多面体间碰撞点的快速算法[J]. 软件学报, 1999, 10(12)： 1253-1258.

[5] 任世军, 洪炳熔, 孟庆鑫. 判断两个凸多面体是否相交的一个快速算法[J]. 软件学报, 2000, 11(4)： 563-568.

[6] Moore M, Wilhelms J. Collision detection and response fir computer animation [J]. Computer Graphics, 1988, 22(4)： 289-298.

[7] Rogers D F. Procedural elements for computer graphics [M]. New York： McGraw-Hill Book Company, 1985. 205-212.

[8] Baraff D. Analytical methods for dynamics simulation of non2penetrating rigid bodies [J]. Computer Graphics, 1989, 23(3)： 223-232.

[9] Herzen B U, Barr A H, Zatz H R. Geometric collisions for time-dependent parametric surfaces [J]. Computer Graphics, 1990, 24(4)： 39-48.

[10] Gottipolu R B, Ghosh Kalyan. An integrated approach to the generation of assembly sequences [J]. International Journal of Computer Applications in Technology, 1995, 8(3-4)： 125-139.

[11] 肖 翔, 尹文生. 一种基于配合约束的装配顺序产生算法[J]. 计算机辅助设计与图形学学报, 2001, (13)： 730-735.