两面多框可构视图中存在不可构表面的条件
2010-01-01周宗团陈翔鹤
周宗团, 曹 敏, 陈翔鹤
(西安工程大学,陕西 西安 710048)
在对可构视图研究的过程中,发现在有些可构视图中存在有不可构表面,也就是说,由这类可构视图构造空间形体时,有某些封闭图框所表达的表面形状始终保持不变。那么,可构视图在满足什么条件时会存在不可构表面呢?如果弄清楚这个问题,不仅可指导人们按照自己的意图设计可构视图,而且可大大提高人们构形设计的速度和准确性。
陈翔鹤曾对文献[1]中可构视图中存在不可构表面的条件进行过研究,指出在单面单框视图、单面多框视图和两面单框视图中均不存在不可构表面,并归纳出在两面多框可构视图中存在不可构表面的条件。但在教学实践的过程中,发现当时归纳的规律有不全面和不严谨的地方,这里对两面多框可构视图中存在不可构表面的条件又重新进行了系统研究和归纳,望同行专家指正。
1 两面多框可构视图中存在不可构表面的条件
(1) 当两面多框可构视图中存在有对称同类形图框时,则该对称同类形图框分别为形体上两个不可构表面[2]。
在这里,对称同类形图框必须具有以下3 个特征:① 图框的边数相同,点对应点、直线对应直线、直角边对应直角边;② 图框上必存在与某投影轴平行的一对应边,且该对应边距所平行的投影轴的距离最近;③ 图框上至少有一对应边与可构视图中同面点集反向倾斜相交或反向倾斜。换句话说,如果设定的两面多框可构视图为主、俯视图时,对称同类形图框上必有一对应边同时平行于X 轴,且该对应边距X 轴距离最近;如果设定的两面多框可构视图为主、左视图时,则对称同类形图框上必有一对应边都平行于Z 轴,且该对应边距Z 轴距离最近;满足以上3个几何特征的封闭图框即为对称同类形图框。
如图1(a)所示的主视图和俯视图是一组两面多框可构视图,该组视图均由两个封闭图框组成且为对称形状,主视图2′、3′两点连线和俯视图1、3 两点连线均与左右两侧的同面点集反向倾斜相交,由于在△153 和△2′3′4′这对对称同类形图框中,图框线1、5 和图框线2′、4′都平行X 轴(15//2′4′//X 轴),且两图框线距离X 轴最近,因此,a′和b 两封闭图框为对称同类形图框,它们是形体上两个不可构表面。通过进一步分析可以看出,a′和b 两封闭图框是形体上两个不同表面的投影,如A 面为一正平面,B 面为一水平面,因此,在构造空间形体时,该对称同类形图框所表达的表面形状始终保持不变,如图1 所示[3]。
在图1 所示视图中的另外两个封闭图框△123和△1′2′3′中,虽然也有一对应边平行X 轴(1′3′//23//X 轴),但这两条边到X 轴的距离不是最小,所以△123 和△1′2′3′不是对称同类形图框,它们是对应同类形图框。通过进一步分析可以看出,由于在△123 和△1′2′3′这对对应同类形图框中含有同面点集,因此该对应同类形图框是形体上的可构结构。

图1 存在不可构表面的视图
在图2、图3 和图4 中的a′和b"两封闭图框均满足对称同类形图框的三个条件,因此,a′和b"是对称同类形图框;在图5、图6 和图7 中a′和b 两封闭图框也为对称同类形图框,它们都是形体上的不可构表面[4]。
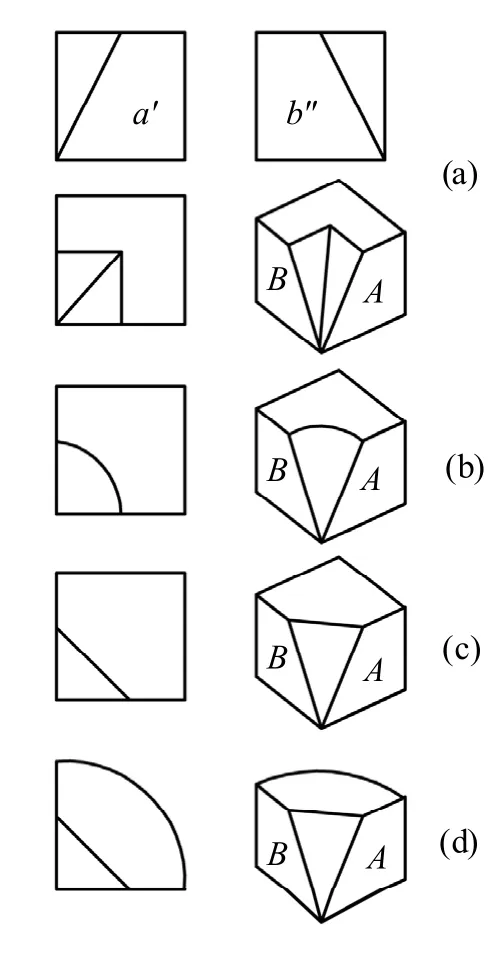
图2 具有对称同类形图框
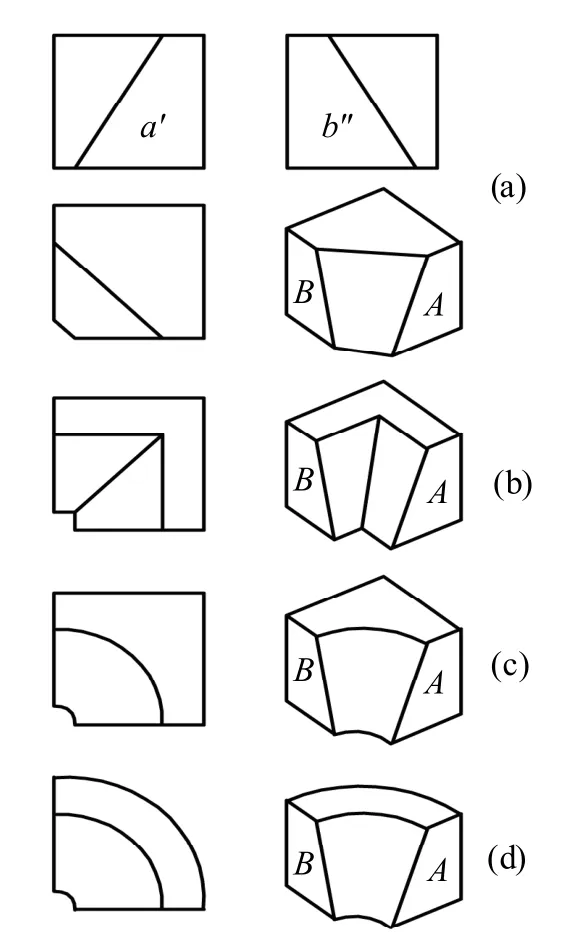
图3 具有对称同类形图框

图4 具有对称同类形图框
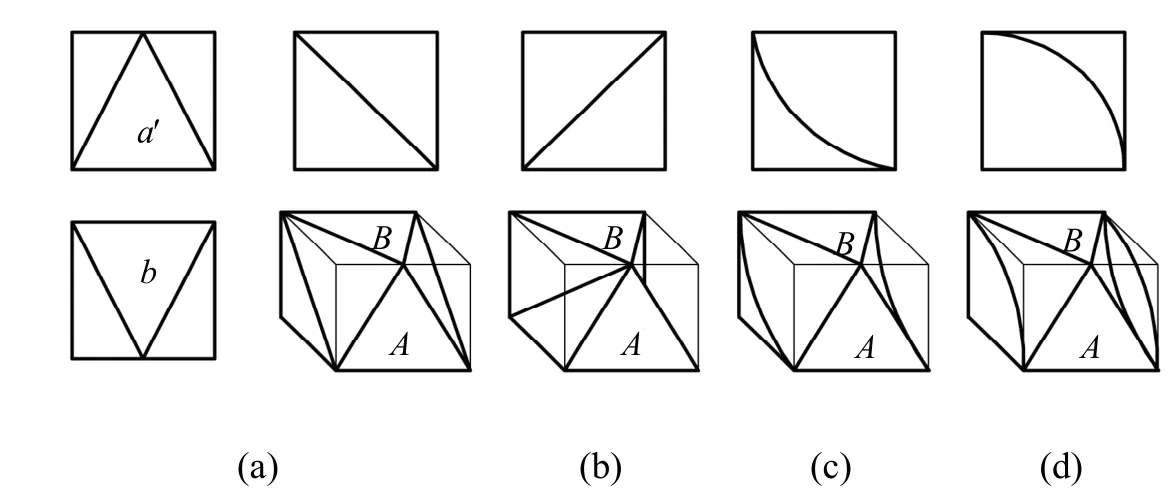
图5 具有对称同类形图框
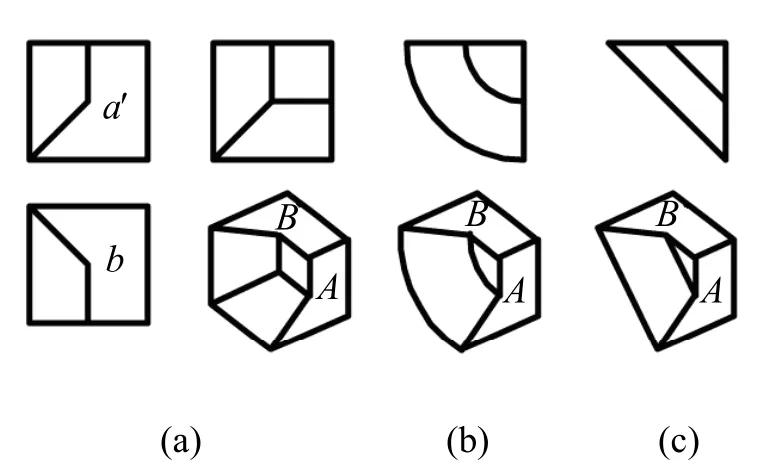
图6 具有对称同类形图框
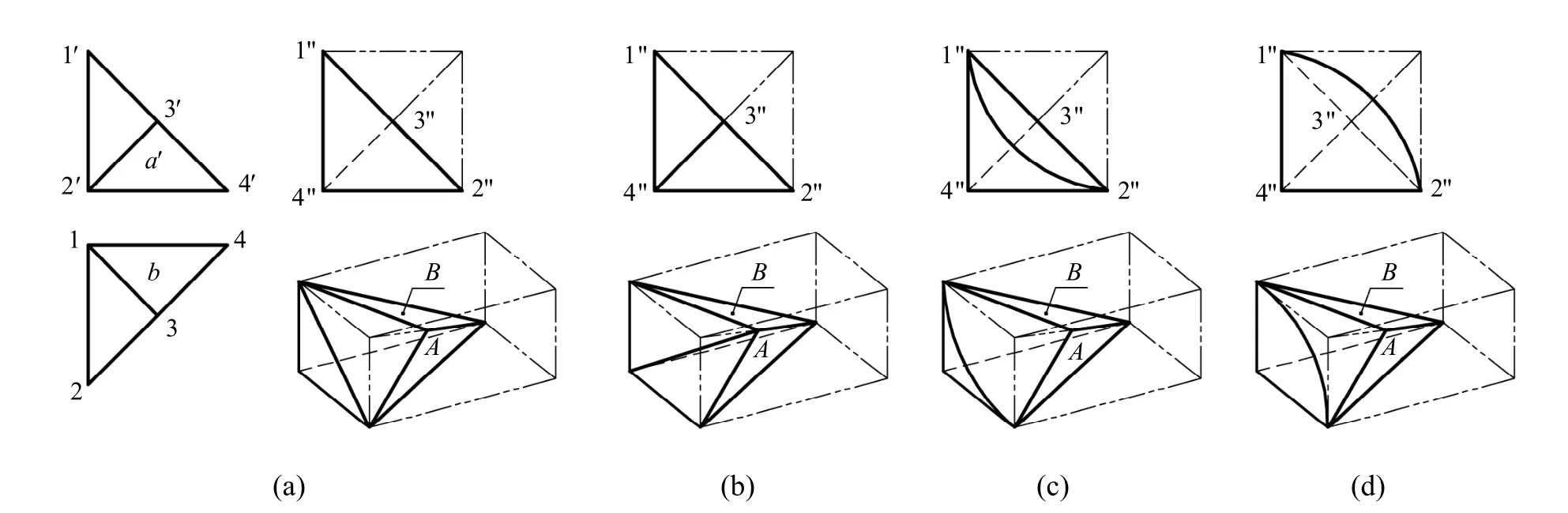
图7 具有对称同类形图框
(2) 当两面多框可构视图中存在不含有同面点集的对应同类形图框时,则该对应同类形图框为形体上一个不可构表面(对应同类形图框的定义与文献[5]完全相同)。
如图8 所示,a′和a 是一对不含同面点集的对应三角形,它们是形体上同一个面的两个投影,因此,在构造空间形体时,该对应同类形图框所表达的表面形状始终保持不变。而其余两个对应封闭图框,均为含有同面点集的对应三角 形图框,因此它们是视图中的可构结构。

图8 不含同面点集的对应同类形图框
图9 所示的a′和a 也是一对不含同面点集的对应梯形,它们也是形体上同一个面的两个投影,因此,在构造空间形体时,该对应同类形图框所表达的表面形状始终保持不变。
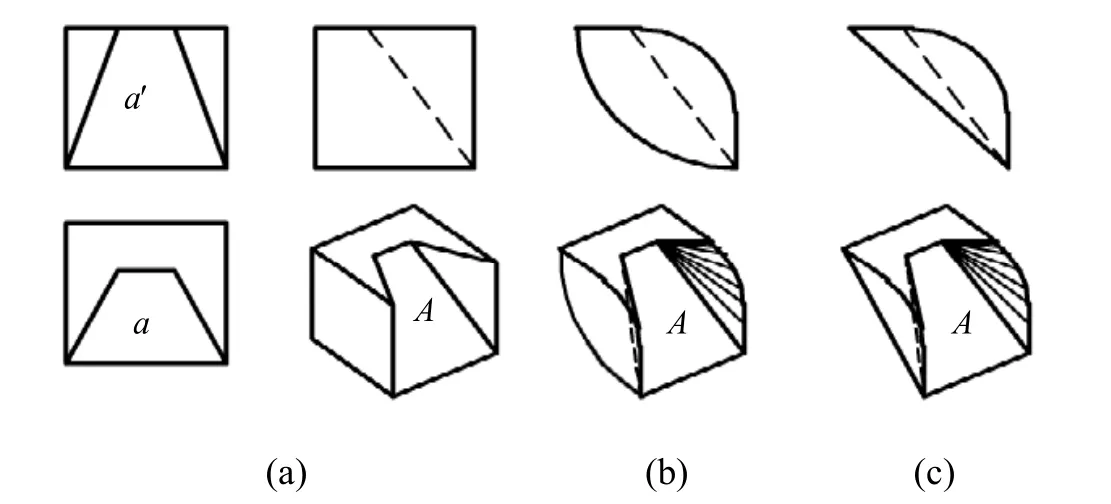
图9 不含同面点集的对应同类形图框
(3) 当两面多框可构视图中存在含有同面点集的非三角形的对应多边同类形图框,且该图框线中至少有一对应边与同面点集倾斜或斜交时,则该对应同类形图框亦为形体上的一个不可构表面。
如图10 所示的a′和a 为含有同面点集对应五边同类形图框,且两封闭图框中有一条图框线与一同面点集斜交, 因此,在构造空间形体时,该对应同类形图框所表达的表面形状也始终保持不变。图11 所示的b′和b"两封闭图框和图12所示的c′和c 两封闭图框虽然都含有同面点集,但在各封闭图框图中至少有一条图框线与同面点集倾斜,因此,在构造空间形体时,该对应同类形图框所表达的表面形状也始终保持不变。
(4) 当一投影直线与一封闭图框对应,且该封闭图框线不与视图中两同面点集出现部分重合时,该封闭图框亦为不可构表面。
由正投影原理可知,当一封闭图框与一投影直线对应时,所表示的空间平面有两种情况:一是当投影直线处于平行于某投影轴线时,该投影直线表示的是投影面平行面;二是当投影直线倾斜于某投影轴线时,表示的是投影面垂直面;因此,这时该封闭图框所表示的平面均为不可构表面。如图13 所示,B、C、D、E、F 面均为不可构表面,其中B、C 为对称同类形图框;D、E面均为投影面平行面;F 面是一铅垂面。而A 是含有同面点集的对应三角形图框,因此该对应同类形图框是形体上的可构结构。
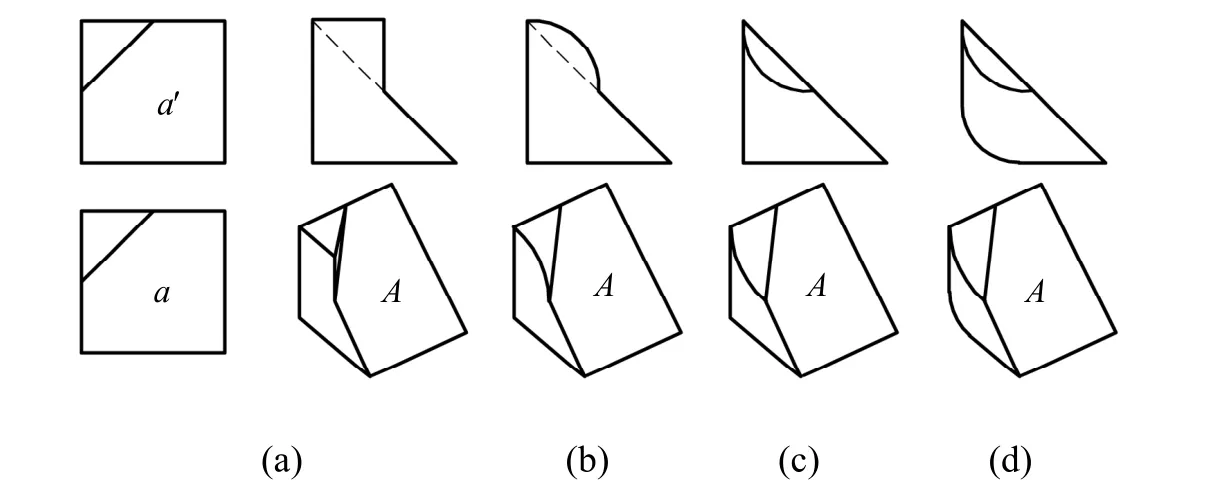
图10 含同面点集的对应多边同类形图框

图11 含同面点集的对应多边同类形图框

图12 含同面点集的对应多边同类形图框
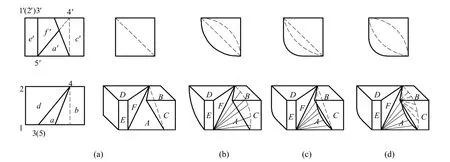
图13 封闭图框与一投影直线对应
在图14 所示中的C、D 面均为不可构表面,其中C 为一对应同类形图框;D 是一直线对应封闭图框的水平面。值得注意的是,虽然E 也是一直线对应一封闭图框,但由于该封闭图框的左右两边线与视图中的外轮廓的两同面点集出现部分重合,因此,这时E 面是可构表面而非不可构表面。而A、B 是含有同面点集的对应三角形图框和矩形图框,因此该两个对应同类形图框是形体上的可构结构[6]。
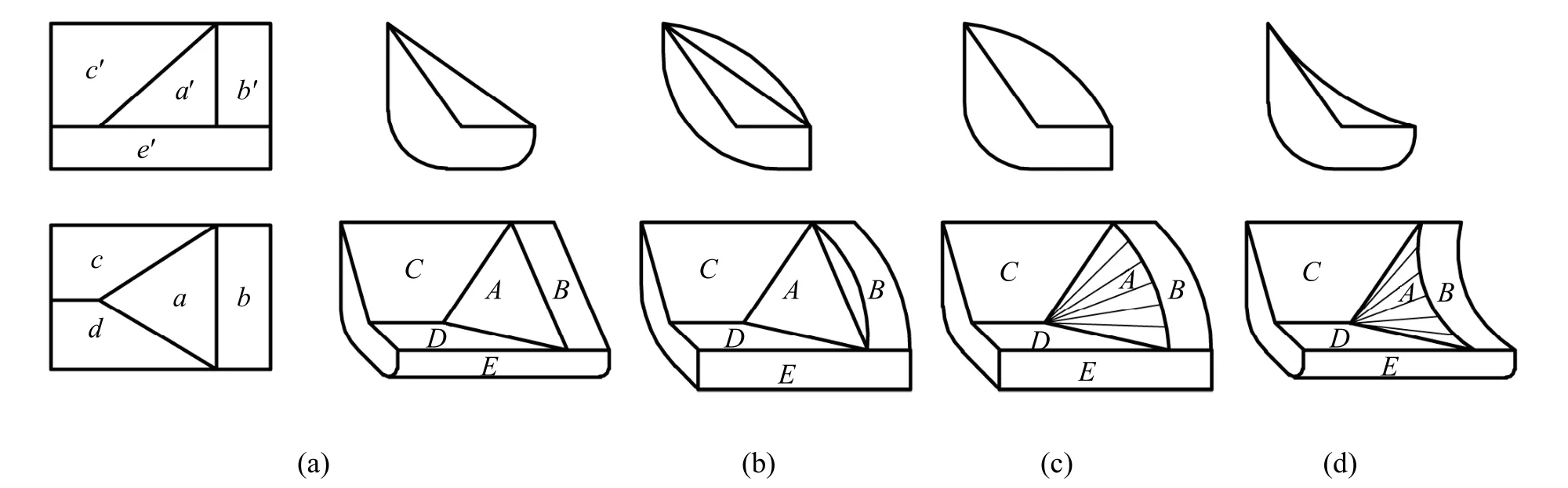
图14 封闭图框线与视图中两同面点集重合
2 结 论
通过以上对两面多框可构视图中存在不可构表面的条件的分析,可得出以下结论:
(1) 当两面多框可构视图中存在有对称同类形图框时,则该对称同类形图框分别为形体上两个不可构表面;
(2) 当两面多框可构视图中存在不含有同面点集的对应同类形图框时,则该对应同类形图框亦为不可构表面。
(3) 当两面多框可构视图中存在含有同面点集的非三角形的对应多边同类形图框,且该图框线中至少有一对应边与同面点集倾斜或斜交时,则该对应同类形图框亦为不可构表面。
(4) 当一投影直线与一封闭图框对应,且该封闭图框线不与视图中两同面点集出现部分重合时,该封闭图框亦为不可构表面。
[1] 陈翔鹤. 可构视图中存在不可构表面的条件[J]. 华中师范大学学报(自然科学版), 2006, (4): 61-63.
[2] 陈翔鹤. 常见不定形投影及其空间构形分析[J]. 陕西工学院学报, 1998, (1): 83-87.
[3] 陈翔鹤, 陆国栋. 两面可构视图的空间构形方法研究[J]. 工程图学学报, 2006, 27(3): 151-155.
[4] [苏联]A C 普加切夫著. 制图思考题200 例[M]. 叶 蕊译. 北京: 北京出版社, 1990. 13-34.
[5] 陈翔鹤, 陆国栋. 视图的可构性分析及其空间构形方法研究[J]. 工程图学学报, 2006, 27(3): 146-150.
[6] 陈翔鹤. 存在不可构表面的可构视图的构形设计方法[J]. 西安工程科技学院学报, 2006, (4): 475-477.
