3D 非均匀直线网格GPU 体绘制方法研究

袁 斌

（北京应用物理与计算数学研究所，北京 100088）

在医学、计算物理等领域涉及大规模的体数据集，需要合适的可视化技术。体绘制技术是重要的可视化技术之一。体绘制的研究多集中于无结构数据场和均匀数据场的研究，比如，对于均匀数据场有光线投射方法[1]，shear-warp 方法[2]，纹理体绘制方法[3−5]和GPU 光线投射方法[6−9]。Steven P 采用k-buffer 较好地实现了无结构数据场体绘制[10]。

可编程图形处理器GPU 是特殊的SIMD 硬件，提供了片元编程技术，它提供了许多SIMD指令[11]。SIMD 是单指令多数据的并行机制。SIMD 技术适合于3D 数据场的绘制，3D 点的位置可以用坐标向量(x, y, z)表示，也可以用齐次坐标向量(x, y, z, w)表示，而颜色用向量(r, g, b, a)表示。图形数据很适合于用向量表示，在图形绘制中采用SIMD 技术是很自然的事情。借助于纹理映射，在片元处理阶段，可以进行光线积分。GPU 光线投射方法可以看作光栅化方法和光线投射方法结合的方法，在GPU 中, 首先要绘制三角面片，才能执行相应的片元处理。基于GPU片元编程的算法是一种SIMD 算法。

在目前的3D 科学计算中经常使用非均匀直线网格(Non-uniform Rectilinear Grid)，它根据物理量的变化自适应地调整网格间隔。非均匀直线网格与均匀网格的区别在于，它的每个方向的网格间隔是变化的。在CPU 光线积分中，需要判别采样点所在的位置，对于均匀网格很容易通过简单的取整计算即可以实现，对于非均匀网格不能采用这种方法。在GPU 体绘制中，纹理图像相当于均匀网格，它不能直接表示非均匀网格。因而，无法使用目前业已存在的针对均匀网格的基于切片的纹理体绘制方法和GPU 光线投射方法。一般处理办法是将非均匀直线网格转换成均匀网格, 然后利用这两种方法进行体绘制。但是，这样会导致数据量大大增加，并且需要重采样，必然会花费相当的计算时间和带来一定的误差。这里以Lared-S 密度数据（非均匀直线网格）为例，来说明这一点。它的节点数为220×80×80，如果把它转换成均匀网格，为了减小失真，在每个方向上，均匀网格的网格间距必须不大于原网格最小间距的一半，这样网格节点至少为15250×159×159，是原来网格的273.8 倍。这里均匀网格梯度计算的时间必然远大于原网格梯度计算的时间，而且重采样需要花费大量的计算时间。因而，研究针对非均匀直线网格的GPU 体绘制方法是很有意义的。

本文首先给出针对非均匀直线网格的CPU光线投射方法，一方面它为后面的内容作铺垫，另一方面可以用来比较。接着给出针对非均匀直线网格的基于辅助纹理的GPU 光线投射和基于切片的3D 纹理体绘制方法。最后，对这些方法进行了比较分析。

1 针对非均匀直线网格的CPU 光线投射方法

本文先给出针对非均匀直线网格的CPU 光线投射方法。

光线投射方法的基本思想是，对每个像素发出一条光线，沿光线进行光亮度积分。在光线积分过程中，沿光线进行均匀采样。当光线跨出数据包围盒，或不透明度接近1，停止追踪。对于非均匀直线网格，在光线积分过程中，借助均匀的辅助网格，快速确定采样点所在的单元。

辅助网格的设计应该使它具有最少的存储量和最简单的计算形式。按照这种想法，本文中使用的辅助网格，是隐式网格，它的每个网格单元或节点并不占用内存。辅助网格的网格面与原网格的网格面平行，辅助网格的每个方向的网格间隔应该小于非均匀网格的相应方向的最小网格间隔，这样在每个方向上，辅助网格单元至多与原网格的1 个网格面相交。设辅助网格的尺寸为nx×ny×nz。非均匀直线网格的坐标数组（或称为坐标向量）为X, Y, Z 在实际计算中，需要把它们变换到辅助网格的体素空间。这里需要3 个索引数组xindex，yindex，zindex（它们的数组元素的个数分别为nx, ny, nz），分别定义为

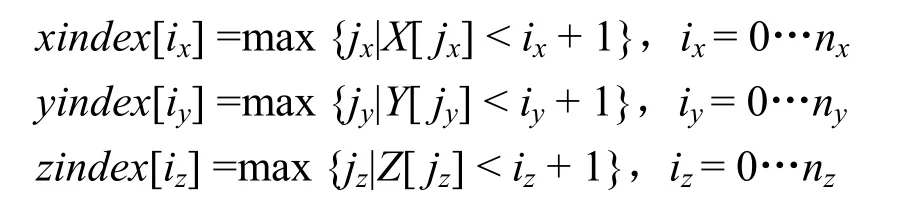
例如，如图1 所示，非均匀直线网格的边界与辅助网格的边界重合，实线为非均匀网格的网格线，虚线为辅助网格的网格线，xindex[0] =0，xindex[1]=1，xindex[2]= index[3]=2。按照这个定义，每个索引只保存一个整数值。在实际计算中，xindex 用O(n)的算法实现：

yindex，zindex 采用类似的方法计算。

实现辅助网格占用的空间为O(nx+ ny+ nz)，而不是O(nx×ny×nz)。

在光线积分过程中，先通过取整，计算采样点所在的辅助网格单元，再利用索引快速发现采样点所在的直线网格单元，光线的当前采样点的位置为(xs, ys, zs)。通过如下方法得到的(icx, icy, icz)，即是采样点所在单元的结构坐标。

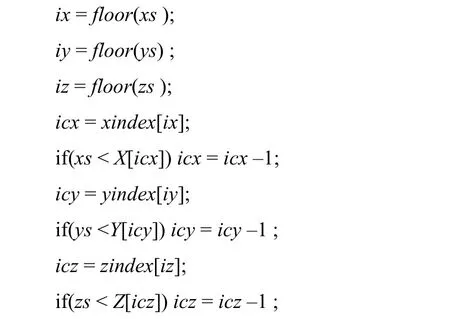
然后，进行插值计算，通过查表计算不透明度，如果不透明度不为0，通过查表计算光照效果，累积颜色和不透明度。在这个算法中，单元(xindex[ix], yindex[iy], zindex[iz])称为推荐单元；当前采样点所在的单元，称为当前单元。推荐单元未必是当前单元，通过修正得到当前单元。

非均匀直线网格中，节点(i, j, k)的梯度采用如下的加权差分公式计算，梯度作为法向量用于光照计算，采用Phone 的光照模型，这样光照效果反映了数据的局部变化。

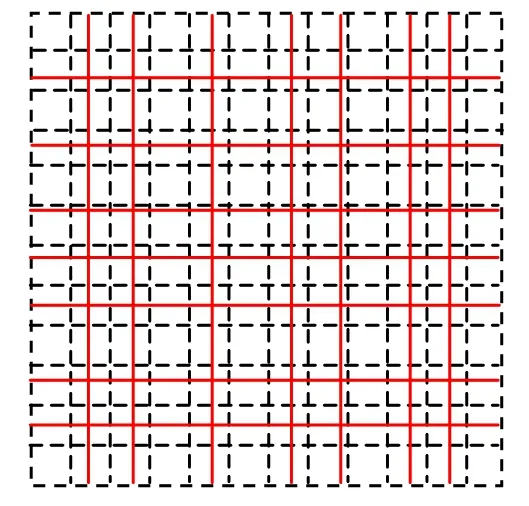
图1 辅助网格

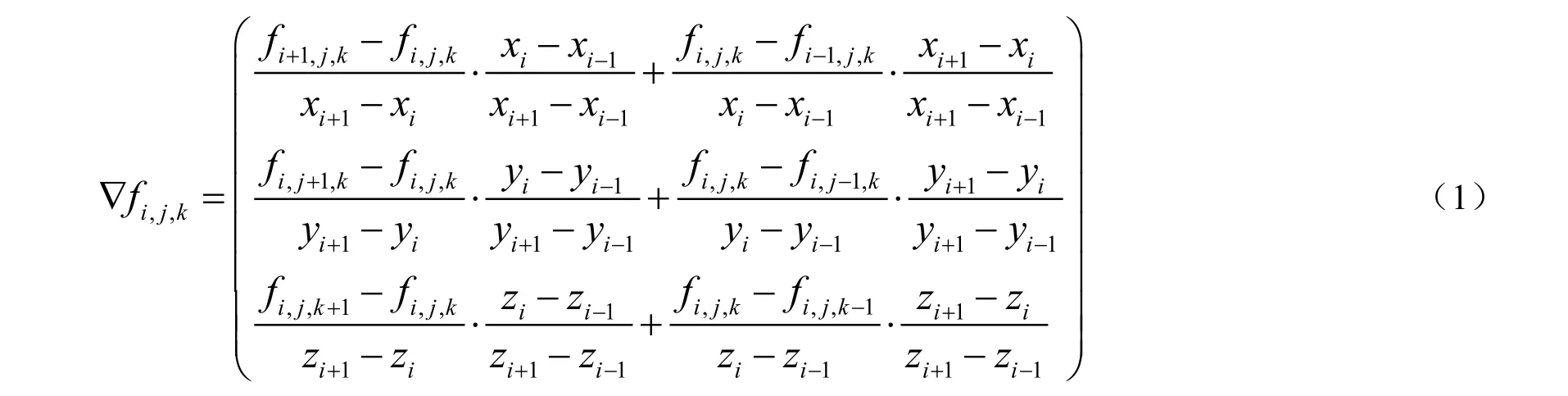
在体绘制中有些数据的不透明度值为0，对体绘制积分没有任何贡献，视为无效数据。包含所有有效单元的最小长方体，称为有效区域。在绘制时只对有效区域进行绘制。这样不访问无用的单元，大大提高性能。本文只对有效区域内的光线段进行体绘制积分，这样可以忽略大片的空白区域，加快绘制速度。

在体绘制时按照Nyquist 采样定理，光线上采样点的间隔取为最小网格间隔的一半。如果要得到更精确的图像可以用更小的采样间隔。

2 针对非均匀直线网格的GPU 体绘制方法

2.1 GPU 光线投射方法

GPU 的光线投射的基本步骤是：

（1） 把数据场装入GPU 内存；

（2） 装入片元程序；

（3） 设置片元程序的输入参数；

（4） 启用片元程序；

（5） 绘制有效数据体包围盒的前表面。

在对一个数据场进行交互绘制时，只在第一次绘制时需要数据装入操作。为了加快绘制，只绘制有效区域，因而只需装入有效区域的数据。通过绘制有效数据体包围盒的前表面，对它所覆盖的每个片元(fragment)，调用片元程序，进行光线积分。在光线积分过程中，需要计算每个采样点的标量值和梯度值，然后通过查传输函数获得采样点的材质（Material，包括颜色和不透明度），采用Phone 的光照模型计算颜色，并进行累积。对于均匀网格，在把标量数据和梯度数据装入纹理内存后，可以直接通过纹理映射快速计算每个采样点的标量值和梯度值。然而，对于非均匀直线网格需要借助于辅助纹理来完成这一过程。

对于模型空间V（或称为物理空间）内的非均直线网格R，可以通过“挤压变换”T 强制其间隔均等，使R 变成一个均匀网格S，它作为三维纹理图像装入GPU 内存，该纹理空间记为Q，纹理装入实现了一个线性变换M，把S 映射为Q中的均匀网格，不妨表示为MTR，MTR 的每个节点为纹元(texel)的中心。T 是一个非线性变换，但它是分段线性变换, 当它约束到每个单元空间，即为线性变换。R 的辅助网格A 是模型空间V 中的均匀网格，在实际计算时，需要用线性变换L，把A 变换成辅助纹理空间B 中的均匀网格，记为LA。用L 把R 变换到B，仍然得到一个非均匀直线网格，不妨用LR 表示。A 的体素(voxel)空间为C，变换H 把A 变换为C 中的间隔为1的均匀网格；H 把R 变换到C，仍然得到一个非均匀直线网格，不妨用HR 表示。MTL－1是非线性变换，它可以把辅助纹理空间B 中采样点的坐标转换为Q 中的坐标，进而通过纹理映射得到标量和梯度。

对每个方向只要一维的辅助纹理，它保存原网格的索引，称为索引纹理，这里索引纹理的尺寸应该为2 的幂。每个索引纹理保存MTR 的垂直于相应坐标轴的网格面的截距。在此，xindex的定义修正为

这里，X 是HR 的坐标向量。

yindex, zindex 的定义和计算方法也要作相应修正。

由于GPU 中纹理的最大尺寸为4096。而辅助网格的尺寸会超过这个值，因此，把索引信息均分成几段，每一段作为2D 纹理的一行，这样把一维纹理折叠成2 维纹理。3 个方向的索引纹理的高度分别用xh, yh, zh 表示，辅助纹理空间B为[0, xh]×[0, yh]×[0, zh]，绘制有效区域时，其包围盒顶点的纹理坐标设置为LA 包围盒的顶点坐标。另外，对每个方向，还要有一维纹理保存纹理空间B 中非均匀直线网格LR 的坐标向量，称为坐标纹理。为了保证精度，索引纹理和坐标纹理，均采用32 位浮点纹理，它们的放大和缩小滤波方式均设置为GL_NEAREST。

作者按照公式(1)计算梯度量和梯度，保存到3D 纹理图像中；把标量和梯度数据装入GPU 内存。此外，还要把索引纹理和坐标纹理装入到GPU 内存。在片元程序中，在辅助纹理空间B中进行积分。在光线积分中，对每个采样点p，计算MTL－1p，得到Q 中的纹理坐标，通过纹理映射得到标量值和梯度，由传输函数（用纹理表示）得到采样点的材质，通过光照计算得到采样点的颜色，累积颜色和不透明度。

在直线网格中，单元(i, j, k)有8 个顶点，均为网格节点；其中，节点(i, j, k)称为它的第一顶点，节点(i+1, j+1, k+1)称为它的第8 顶点。计算变换MTL－1的算法思想是，根据光线采样点的坐标查索引纹理，查得推荐单元第一顶点在纹理空间Q 中的坐标，保存到t1，通过LR 的坐标向量纹理，由t1 查得第一顶点在B 中的坐标，把它与当前采样点的坐标比较，修正t1 得到当前单元的第一顶点在Q 中的纹理坐标，计算当前单元的第8 顶点在Q 中的纹理坐标tb；通过LR 的坐标向量纹理，由t1 查得当前单元第一顶点在B 中的坐标a，第8 顶点在B 中的纹理坐标b，计算当前采样点在当前单元中的插值参数；进而计算当前采样点在Q 中的纹理坐标。下面给出具体算法，这是向量算法。索引纹理映射可以用函数XIndex(v), YIndex(v), ZIndex(v)表示，v 是向量，为2D 纹理坐标。spacing.x, spacing.y, spacing.z分别表示Q 中s, t, r 方向相邻纹元的间隔。这里用X(s), Y(s), Z(s)表示直线网格LR 的坐标向量纹理映射，s 为1D 纹理坐标。如果操作数为向量，+, – ,*, / 为向量运算。a.x, b.x 等为标量，无“.”的变量为4 维向量。向量函数SLT(u, v)表示向量比较指令SLT[11]。texcoord 为辅助纹理坐标。向量函数fraction(v)取v 的每个分量的小数部分，向量函数floor(v)取v 的每个分量的整数部分。算法如下：

算法1 计算变换MTL-1的算法

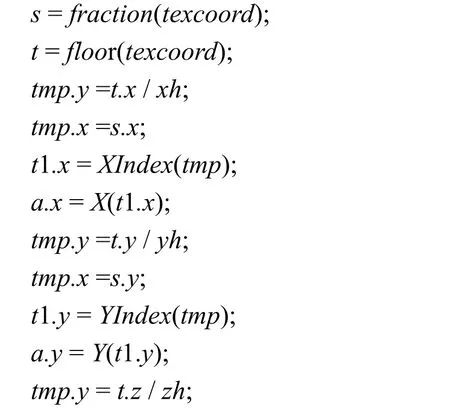
用算法1 计算出t1 后，用t1 通过纹理映射查询标量值和梯度值。

光线积分在辅助纹理空间B 中进行，需要对采样步长进行修正。下面说明这一点。

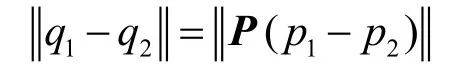
由此可见，在透视变换下，如果在LA 中，采用同样的步长进行采样，不同方向的光线在模型空间V 中的相应采样步长很可能不同。因此，要使得各方向光线的采样步长变换到模型空间V中保持相同，必须在B 中根据光线方向计算采样步长。设在辅助纹理空间B 中光线方向为v（单位向量），在模型空间V 中设定采样步长为d，那么，该光线在辅助纹理空间B 中的采样步长是

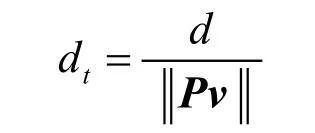
首先实现了针对均匀网格的GPU 光线投射方法，在实现过程中，参考了S Stegmaier 等人的片元程序[6]和vtk[12]的3D 纹理体绘制中的片元程序。整个光线投射算法是用ARB fp1 汇编语 言[11]实现，为了采用分支命令和循环命令，在程序开头加上OPTION NV_fragment_program2。在实现的用于光线积分的片元程序中采用了光线早终止技术，只要累积不透明度大于0.98, 就终止光线积分，这样节省计算。如果采样点的透明度为0，则跳过采样点，不进行光照计算，这样也可以节省计算。在此基础上，把前面的算法1用ARB fp1 汇编语言实现，并插入到光线积分循环中每步的开头，从而实现了基于辅助网格的针对非均匀直线网格的GPU 光线投射方法。

算法采用标量传输函数（它把采样点的标量转换成颜色和不透明度）和梯度量传输函数（它把梯度量转换成调制因子）。算法用数组表示传输函数，并装入一维纹理，这样通过纹理映射实现传输函数。通过采用梯度量调制，可以突出梯度变化大的区域，使物质分界面更清晰。

2.2 基于切片的3D 纹理体绘制方法

作者又把2.1 节的算法与基于切片的3D 纹理体绘制算法结合，得到针对非均匀直线网格的3D 纹理体绘制方法。在该算法中不必对采样步长进行校正。算法中所用的切片平行于视平面。为了提高绘制精度，切片的间隔为最小网格间隔的一半。

3 结果与结论

作者实现了针对非均匀直线网格的CPU 光线投射和GPU 光线投射，以及基于切片的3D 纹理体绘制。为了便于描述，在下文中分别简称为GPU 光线投射，CPU 光线投射和3D 纹理体绘制。

在Intel P4 3.0GHz 的机器上测试上述算法，它装有Nvidia Geforce 6800GT 图形卡。在测试中GPU 光线投射和CPU 光线投射采用一致的采样步长(即把两种方法的采样点映射到同样的坐标系下，两者的采样步长是相等的)，相当于3D 纹理体绘制中相邻切片的距离。为了保证绘制质量，采样步长均为最小网格间隔的一半。

如图2，对于vtk 的非均匀直线网格RectGrid数据进行绘制，数据尺寸47×33×44，图像尺寸（视区尺寸）512×512，采用初始传输函数。CPU光线投射方法绘制时间6.375 秒, 最大积分步数156。如图2(b)，GPU 光线投射，绘制时间0.265秒。如图2(d)所示，用3D 纹理体绘制方法，绘制到普通帧缓存，图像质量较差，这是由于普通帧缓存，R、G、B、A 分量各占8 位，因而精度不够, 当不透明度小于1/256 时，便被忽略，不能正确累积颜色。解决办法是将图像绘制到浮点缓存中，再把浮点缓存绑定到纹理，再通过片元程序把纹理绘制到普通帧缓存中。每次绘制切片需要采用图形流水线中的混合操作，把颜色累计到浮点缓存中。采用Pbuffer 实现浮点缓存。Nvidia Geforce 6800GT 的混合操作运算是16 位的浮点运算[13]，把Pbuffer 配置成浮点缓存，并且每个颜色分量配置成16 位浮点数，这样，其计算精度必然低于光线投射方法。图2(c)是采用16 位浮点缓存的3D 纹理体绘制结果，绘制时间0.093 秒，切片数155。在这里，图2(a)，图2(b)， 图2(c)图像质量相当。图2(f)的质量低于图2(e)，这说明3D 纹理体绘制，即使采用了16 位浮点缓存，其图像质量仍低于GPU 光线投射。

在后面的测试结果中，如果没有特别声明，基于切片的3D 纹理绘制采用16 位浮点缓存。

图3 是Lared-S 密度数据（非均匀直线网格）的绘制结果，数据尺寸220×80×80，图像尺寸512×512，为绘制这个图像，调整了传输函数，对数据进行多次平移和旋转变换。图3(a)是CPU光线投射方法的图像，绘制时间16.578 秒。光线积分步数是708。图3(b)是GPU 光线投射图像，绘制时间0.843 秒。图3(c)是3D 纹理体绘制算法绘制的图像。绘制这幅图像，用了1112 个切片，绘制时间0.39 秒。前两幅图像质量相当，（把图像放大后可以看出）3D 纹理体绘制图像质量稍差一些。

把均匀网格数据Hydrogen 和fish，按照正弦函数调整x 方向的网格间隔，得到非均匀直线网格数据，RectHydrogen，Rectfish。这里用RectHydrogen 和Rectfish 对算法进行测试。

Rectfish 数据尺寸256×256×512，图像尺寸512×512，图4(a)采用CPU 光线投射，绘制时间18.797 秒，最大积分步数637；图4(b)采用GPU光线投射方法，绘制时间1.218 秒；图4(c)采用3D 纹理体绘制方法，绘制时间0.671 秒，切片数758。图4(b)比图4(a)稍有差别，因为梯度的编码方法有所不同。图4(b)与图4(c)质量相当，但后者绘制速度更快一些。

RectHydrogen 数据尺寸128×128×128，图像尺寸512×512，图5(a)采用GPU 光线投射方法，绘制时间1.062 秒；图5(b)和图5(c)采用3D纹理体绘制方法，切片数741，图5(b)使用的绘制缓冲区的每个颜色分量为16 位浮点数，绘制时间0.593 秒；图5(c)使用的绘制缓冲区的每个颜色分量为8 位整数，绘制时间0.593 秒。图5(b)与图5(a)质量相当，图5(c)的质量较差一些。

图2 RectGrid 数据

图3 Lared-S 密度数据

图4 Rectfish 数据

图5 RectHydrogen 数据

采用GPU 光线投射具有与CPU 方法相似的精度，而绘制速度得到大幅度提高。一般情况下，3D 纹理体绘制比GPU 光线投射快，但GPU 光线投射可以获得更好的精度。在GPU 光线积分算法中，一旦累积不透明度超过0.98 即终止光线积分，并且只对不透明的采样点计算光照，这样整体的计算量小于3D 纹理绘制的计算量，但GPU 光线投射绘制的速度却小于3D 纹理体绘制的速度，这是因为GPU 拥有多条片元处理流水线，在GPU 光线投射算法中，各个片元处理流水线的负载严重不平衡，而在3D 纹理体绘制中各流水线的负载基本平衡。这说明片元处理流水线之间的负载平衡对于GPU 绘制是十分有意义的。

对于较大规模的数据场，绘制大幅面的精确图像，其速度仍难达到交互。有两种方法解决这个问题：一是降低数据的分辨率，另一个是降低图像的分辨率。对于后者，可以先绘制到Pbuffer， 然后把它连接到纹理，通过纹理映射绘制大幅面的图像。

[1] Marc Levoy. Efficient ray tracing for volume data [J]. ACM Transactions on Graphics, 1990, 9(3)： 245-261.

[2] Philippe Lacroute, Marc Levoy. Fast volume rendering using a shear-warp factorization of the viewing transformation [C]//Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques. New York, NY, USA, ACM Press, 1994： 451-458.

[3] Brian Cabral, Nancy Cam, Jim Foran. Accelerated volume rendering and tomographic reconstruction using texture mapping hardware [C]//Proceedings of the 1994 Symposium on Volume Visualization. New York, NY, USA, ACM Press, 1994： 91-98.

[4] Klaus Engel, Martin Kraus, Thomas Ertl. High-quality pre-integrated volume rendering using hardware- accelerated pixel shading [C]//Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Workshop on Graphics Hardware, 2001： 9-16.

[5] 童 欣, 唐泽圣. 基于空间跳跃的三维纹理硬件体绘制算法[J]. 计算机学报, 1998, 21(9)： 807-812.

[6] Stegmaier S, Strengert M, Klein T, et al. A simple and flexible volume rendering framework for graphics- hardware-based raycasting[C]//Proceedings of the International Workshop on Volume Graphics ’05. Stony Brook, New York, USA, 2005： 187-195.

[7] Klein T, Strengert M, Stegmaier S, et al. Exploiting frame-to-frame coherence for accelerating high-quality volume raycasting on graphics hardware [C]// Proceedings of IEEE Visualization '05, 2005, IEE, 2005： 223-230.

[8] 储璟骏, 杨 新, 高 艳. 使用GPU 编程的光线投射体绘制算法[J].计算机辅助设计与图形学学报, 2007, 19(2)： 257-262.

[9] 陈 为, 彭群生, 鲍虎军. 视点相关的层次采样：一种硬件加速体光线投射算法[J]. 软件学报, 2006, 17(3)： 587-601.

[10] CALLAHAN S P, IKITS M, COMBA J L D, et al. Hardware-assisted visibility sorting for unstructured volume rendering [J]. IEEE Transactions on Visualization and Computer Graphics, 2005, 11(3)： 285-295.

[11] NVIDIA. 2007. NVIDIA OpenGL extension specifications[DB/OL]. http：//developer.nvidia.com/ object/nvidia_opengl_specs.html

[12] Martin K, Schroeder W, Lorensen B. The visualization toolKit (VTK) [DB/OL]. http：//www.vtk.org/2008.

[13] Kilgariff E, Fernando R. The GeForce 6 series GPU architecture [M]. GPU Gems 2, Addison-Wesley, 2005. 471-491.