裁剪面的一类参数变换

杨 胜， 雍俊海

（1. 清华大学软件学院，北京 100084； 2. 清华大学计算机科学与技术系，北京 100084； 3. 信息系统安全教育部重点实验室，北京 100084； 4. 信息科学与技术清华大学国家实验室，北京 100084 5. 第三军医大学计算机教研室，重庆 400038）

裁剪面是指定义在参数曲面上的一片单连通区域。作为IGES标准的基本几何体素之一，裁剪面已被广泛应用于实体造型和曲面造型系统,参与各种计算[1-4]。裁剪面的计算是实体造型系统的基础，影响着整个系统的效率和稳定性[5]。

裁剪面的计算，总是受到几何参数表示误差和数值计算误差的影响。目前，参数域曲线一般没有精确的数学表示，常用线段、折线或自由曲线等近似表示。根据曲面上的点计算其对应的参数(又称为反求参数)，数值方法通常存在计算误差；同时，曲面上的点与其参数的对应关系存在一对多的情形（如封闭曲面缝合边上的点或极点，对应多个参数值）。这些因素使得建立或修改裁剪面的拓扑关系相当困难，相应的文献也非常少。因此，寻找稳定处理裁剪面的算法，显得特别重要。

正如文献[6]所指出，许多针对参数曲面的算法，并不适用于裁剪面。对于不同参数表示的互相转换问题，参数曲面着重于重新参数化[7-8]，建立重新参数化公式即可；但裁剪面的表示转换还需要处理：① 计算曲面上曲线对应的参数域曲线；② 重新确定裁剪面的拓扑关系。在此过程中，充分利用原有的拓扑信息、避免重新建立拓扑关系成为转换算法能否稳定的关键。

针对裁剪面的参数表示转换问题，本文首先确定参数变换对表示信息的影响，然后给出几何与拓扑信息一致的参数变换的算法。本文还建立了裁剪球面转换问题的参数变换关系，具体给出了转换问题的解决方法；对于需要数值法反求参数的情形，给出了实现单值映射的算法。

1 裁剪面的参数变换

设I=[0,1], D=I×I, S：D→R3为连续映射，S(D)称为参数曲面（或完整面）；若D1⊂D为单连通区域，S(D1) 称为裁剪（参数）面。根据IGES标 准[9]，裁剪面的表示信息包括：① 对应的参数曲面（完整面）；② 参数曲面上的曲线(边)；③ 映射到边的参数域曲线（环边）；④ 环边的连接关系（环）；⑤ 环之间的包含关系（面）。标准还规定了环的方向：外环为逆时针，内环为顺时针。

裁剪面的参数域信息分为几何与拓扑信息两部分，其中几何信息起决定性作用。一旦修改了参数域的曲线，一般需要重新建立几何元素的拓扑关系。如下定义的参数变换是一种常见的参数修改形式。

定义1 若 f, g：I→I为可逆连续映射，则称T：D→D，(s, t) = T(u, v) = ( f(u), g(v))为参数变换。

设S(u, v)为曲面的一种参数表示。

定义1中的参数变换具有可逆、参数u和v的变换可分离的特点。

命题1 对裁剪面的参数域进行参数变换，该变换具有下述性质：

（1） u（或v）向等参线，经过变换后为s（或t）向等参线；

（2） 不相交的两条曲线，经过变换后也不相交；

（3） 环经过变换后仍为环；

（4） 内环经过变换后仍为内环；

（5） 当f, g 同为增函数或减函数，环方向经过变换后不变；

（6） 若f, g 变换为非线性变换，变换后曲线类型改变。

针对裁剪面参数域曲线表示的特点，特作如下定义。

定义2 设t∈I, C(t)为裁剪面参数域曲线，对C(t)进行变换定义为：

（1） C(t)为等参线 对端点进行变换；

（2） C(t)为折线多边形 对端点和连接点进行变换；

（3） C(t)为自由曲线并且变换为线性变换 对控制点进行变换；

（4） 其他情形 首先离散C(t)为折线多边形，然后对折线多边形的端点和连接点进行变换，最后修改C(t)的曲线类型为折线多边形。

定义3 设t∈I, C(t)和P(t)为参数曲线。如果P(t) = C(1-t)，则称P(t)为C(t)的反转曲线；L = {l1(t), l2(t), …, ln(t)}为参数曲线的有序集合，则称{ln(1-t), ln-1(1-t), …, l1(1-t)}为L的反转。

至此，可得到对裁剪面参数域进行变换的算法。

算法1 裁剪面的参数变换

输 入裁剪面，命题1 中确定的参数变换

输 出变换后的裁剪面

步骤1 对参数域曲线进行变换。

步骤2 如果u 向和v 向变换函数同为增函数或减函数，结束。

步骤3 曲面上的曲线反转（或者调整环边与边的方向关系，如同向→反向，反向→同向）。

步骤4 环反转。

2 裁剪球面的表示转换

二次裁剪面由几何参数表示转换为Nurbs 表示，是裁剪面求交、变形等操作的基础。下面以裁剪球面为例，利用参数变换的方法，实现两种不同参数表示形式的互相转换。

球面的Nurbs 表示，u 向通常采用7 点法表示圆、v 向采用9 点法的半圆表示（见图1）。为此，建立球面参数域的转换关系。

图1 Nurbs 表示圆和半圆

引理1 设单位半圆弧的几何参数表示为

C ( t ) = (cosπ t , sinπ t ), t∈[0,1] 该圆弧的三阶Nurbs 表示为

其中 Ni,2(u)和 Ri,2(u)分别为B 样条基函数和 有理样条基函数，P(u)的控制点、权重和节点向量分别为

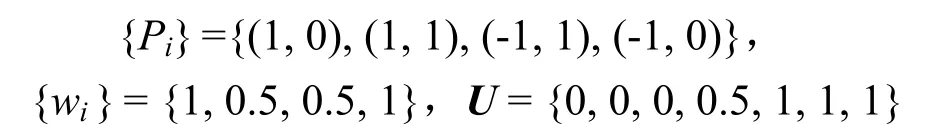
则两种表示方法的参数转换关系为(t, u∈[0,1])

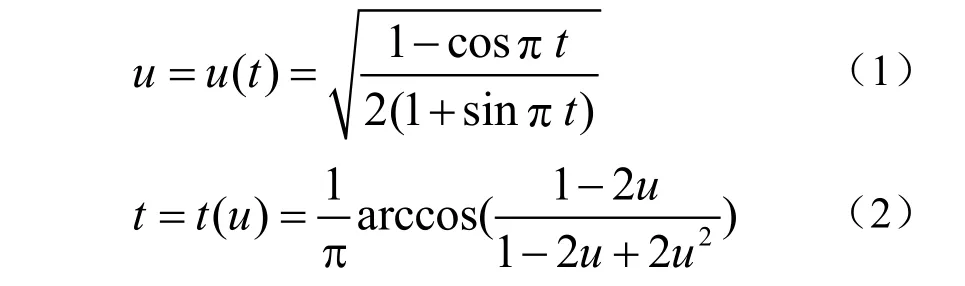
由引理1 以及Nurbs 表示的对称性，可得到单位圆几何参数表示与7 点法Nurbs 表示的参数转换关系。

定理1 设单位圆的几何参数表示为

C ( t ) = (cos2π t , sin 2π t ), t∈[0,1]

该圆的三阶Nurbs 表示为[8-9]

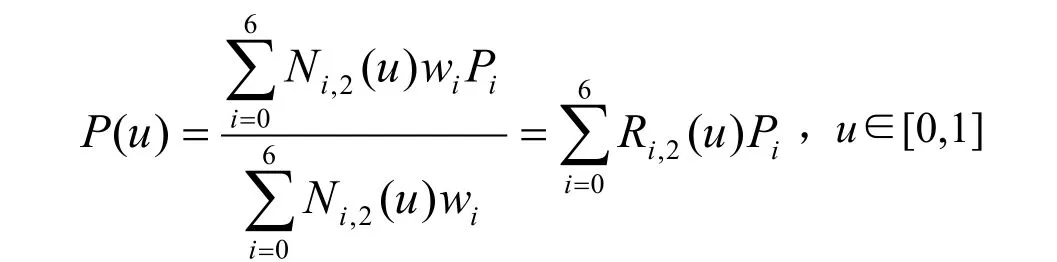
其中 Ni,2(u)和 Ri,2(u)分别为B 样条基函数和 有理样条基函数，控制点、权重和节点向量分别为

{Pi} = {(1, 0), (1, 1), (-1, 1), (-1, 0), (-1,-1), (1,-1), (1,0)}，{wi} = {1, 0.5, 0.5, 1, 0.5, 0.5, 1}，

U = {0, 0, 0, 0.25, 0.5, 0.5, 0.75, 1, 1, 1}

则两种表示方法的参数转换关系为(t, u∈[0,1])

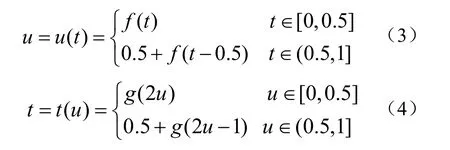
其中

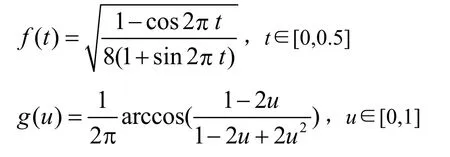
定理1 给出了单位圆几何参数表示转换为Nurbs 表示的参数转换关系。为避免奇异情形的出现，该关系表示为分段函数的形式。同理，可得到半圆的几何参数表示与5 点法Nurbs 表示的参数转换关系。

定理2 设单位半圆弧的几何参数表示为

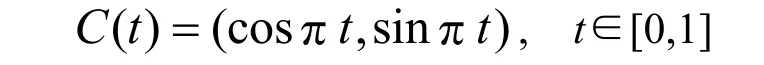
该圆弧的三阶Nurbs 表示为[8-9]

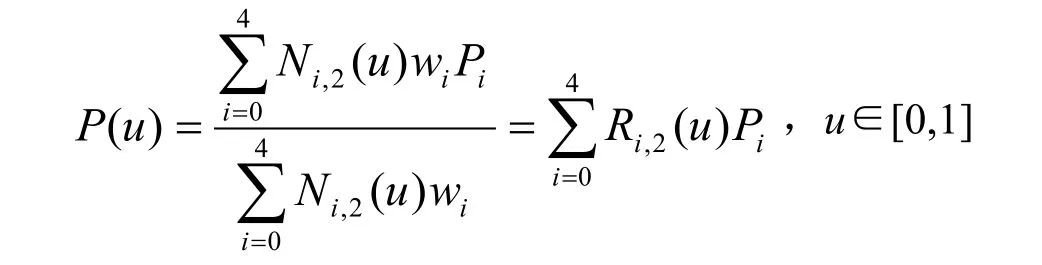
其中 Ni,2(u)和 Ri,2(u)分别为B 样条基函数和 有理样条基函数，控制点、权重和节点向量分别为

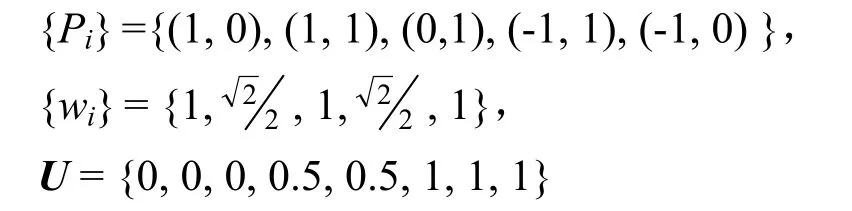
则两种表示方法的参数转换关系为(t, u∈[0,1])

其中

由定理6 和定理7，裁剪球面由几何参数表示转换为Nurbs 表示（参见文献[10-11]），其实现算法如下。

算法2 裁剪球面的几何参数表示转换为Nurbs 表示

输 入几何法表示的裁剪球面

输 出Nurbs 表示的裁剪面

步骤1 修改曲面为Nurbs 表示

步骤2 对参数域进行变换，其中u→s 转换关系为式(3)，v→t 转换关系为式(5)。

同理，裁剪球面由Nurbs 表示转换为几何参数表示，由转换关系式(4)和式(6)可得到相应的转换算法。对于其他复杂的参数表示转换，如裁剪球面转换为高阶的Nurbs 形式，直接给出参数转换的公式相当困难；然而，确定变换函数的单调性却比较容易。不妨设u 向和v 向的变换函数同为增函数，应用命题2 可得出利用数值法计算变换参数的算法，实现参数之间的单值映射。

算法3 数值方法的参数变换

输 入原有曲面表示S(u, v)及其裁剪面上的参数点(u0, v0)，转换后曲面表示P(s, t)。

输 出转换后裁剪面上对应的参数点 (s0, t0)。

计算点Q = S(0.5, v0), 数值法计算s0, t0使得 P(s0, t0) = Q。

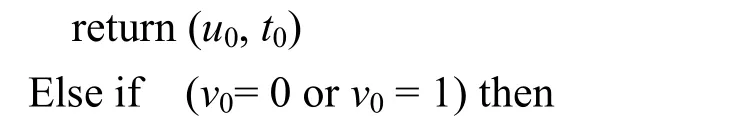
计算点Q = S(u0, 0.5), 数值法计算s0, t0使得P(s0, t0) = Q。

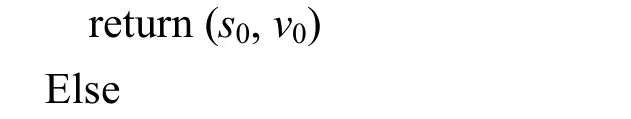
计算点Q = S(u0, v0), 数值法计算s0, t0使得P(s0, t0) = Q。

3 结 束 语

保持裁剪面的形状不改变的前提下，对参数域信息进行修改是实体造型中经常需要的操作。本文由此总结出可逆、u 向和v 向的变换可分离的参数变换。首先，给出了该变换对裁剪面表示信息的影响；然后，提出了对裁剪面参数域进行变换的算法。该算法不需要重新建立裁剪面的拓扑关系，直接对原有数据进行调整，确保了变换后裁剪面几何信息与拓扑信息的一致性。对于不同表示形式的互相转换问题，给出了裁剪球面参数转换公式以及利用参数变换的解决方法，用实例对该算法的有效性进行了验证。

本文提出的参数变换方法，还可以应用到其他二次裁剪面的参数表示转换、裁剪面的镜像变换、裁剪面的合并等问题。下一步拟运用本文的方法处理实体拔模、裁剪面变形等操作下的参数域修改问题。

[1] Casale M S. Free-form solid modeling with trimmed surface patches [J]. IEEE Computer Graphics and Applications, 1987, 7(1)： 33-43.

[2] Farouki R T. Trimmed-surface algorithms for the evaluation and interrogation of solid boundary representations [J]. IBM Journal of Research and Development, 1987, 31(3)： 314-334.

[3] Piegl L A. Geometric method of intersecting natural quadrics represented in trimmed surface form [J]. Computer-Aided Design, 1989, 21(4)： 201-212.

[4] Piegl L A, Richard A M. Tessellating trimmed NURBS surfaces[J]. Computer-Aided Design, 1995, 27(1)： 16-26.

[5] 刘晓强, 唐荣锡. 实体造型技术的现状与发展趋势[J]. 计算机辅助设计与图形学学报, 1997, 9(3)： 284-287.

[6] 胡事民, 孙家广, 汪国昭. 基于广义离散分解trimmed 曲面[J].计算机学报, 1999, 22(3)： 296-301.

[7] Farin G. From conics to NURBS： a tutorial and survey [J]. IEEE Computer Graphics and Applications, 1992, 12(5)： 78-86.

[8] 杨义军, 雍俊海. 有理Bézier 曲面的标准化[J]. 计算机辅助设计与图形学学报, 2007, 19(2)： 245-250.

[9] Reed K. The initial graphics exchange specification (IGES) version 6.0 [S]. NISTIR 4412, National Institute of Standards, 1998.

[10] Piegl L A, Tiller W. The nurbs book [M]. New York： Springer, 1997. 295-307.

[11] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京： 高等教育出版社, 2001. 435-443.