基于NAM的图像集合运算算法及其试验研究
2009-12-04长江大学电子信息学院湖北荆州434023
伍 鹏 (长江大学电子信息学院,湖北 荆州 434023)
陈传波,郑运平 (华中科技大学计算机科学与技术学院, 湖北 武汉 430074)
基于NAM的图像集合运算算法及其试验研究
伍 鹏 (长江大学电子信息学院,湖北 荆州 434023)
陈传波,郑运平 (华中科技大学计算机科学与技术学院, 湖北 武汉 430074)
非对称逆布局图像表示模型是一种新的图像表示方法,由于采用了预定义子模式和非对称的分割方法,获得了较高的表示效率。在NAM基础上,提出了一种实现快速的图像集合运算的新方法,即在导航数组辅助下的分裂组合法,实现了基于NAM的图像集合运算算法,并讨论了算法的时空复杂度。试验结果表明,基于NAM的集合运算算法的执行速度是基于紧凑四元树集合运算算法执行速度的1.291到5.368倍。
图像表示;非对称逆布局模式表示模型;图像集合运算;分裂组合法;紧凑四元树
图像分层表示是数字图像编码中的一个热点问题,各种编码方法层出不穷,但不外乎要解决2个方面的问题:一是为了节省存储空间,实现更高的压缩率;另一个是为了提高运算的速度,实现快速的图像操作。在众多的表示方法中,四元树表示是研究得最早的、也是研究得最多的一种分层表示形式。早期的四元树[1]表示都是基于指针的四元树结构,为了进一步减少存储空间,研究人员针对四元树作了不同程度的改进,比较有代表性的是线性四元树(Linear Quadtree)[2]、四元树的深度优先表示 (DF-Expression Linear Quadtree)[3]和定长线性四元树 (Constant Bit-Length Linear Quadtree, CBLQ)[4]。一般情况下,线性四元树可节省66%的存储空间,特殊情况下可节省高于90%的存储空间。紧凑四元树(Compact Improved Quadtree,简称Compact-IQ)[5]是四元树的最新研究成果,由于采用了只记录灰色结点和熵编码的方法,在压缩率和图像运算效率上都表现非常出色。
非对称逆布局模式表示模型(Non-symmetry Anti-packing Image Representation Model,NAM)[8~10]是一种全新的模式表示方法,可以广泛用于图像、语音、文本和视频等信息模式的表示。尽管相关研究人员围绕NAM提出了多种模式表示和模式操作的算法,但总的来说,在对图像的模式表示上,相对于其他图像表示方法所对应的操作算法而言,还有很多工作需要继续,有些工作还有待进一步完善,基于NAM的集合运算就是其中一种。
图像的集合运算是图像处理中的原子操作,在很多图像处理算法中要直接或间接地调用。笔者充分利用图像中普遍存在的非对称性和相关性,提出了导航数组(Navigation Array, 简称NA)辅助下的分裂组合法(Split and Combination Method,SCM),实现了图像的集合运算。同现有的一些图像表示方法下的集合运算相比,新的集合运算算法由于采用非对称分割所形成的较少的子模式数,在性能上表现突出,它能够极大地提高集合运算的运行速度,使得调用该集合运算算法的程序能够得以快速执行。总之,新算法是图像集合运算上的一个创新,所提出的导航数组以及分裂组合法还可以应用到其他图像处理中,因此既具有理论上的指导意义又具有实践上的应用价值。
1 分裂组合法
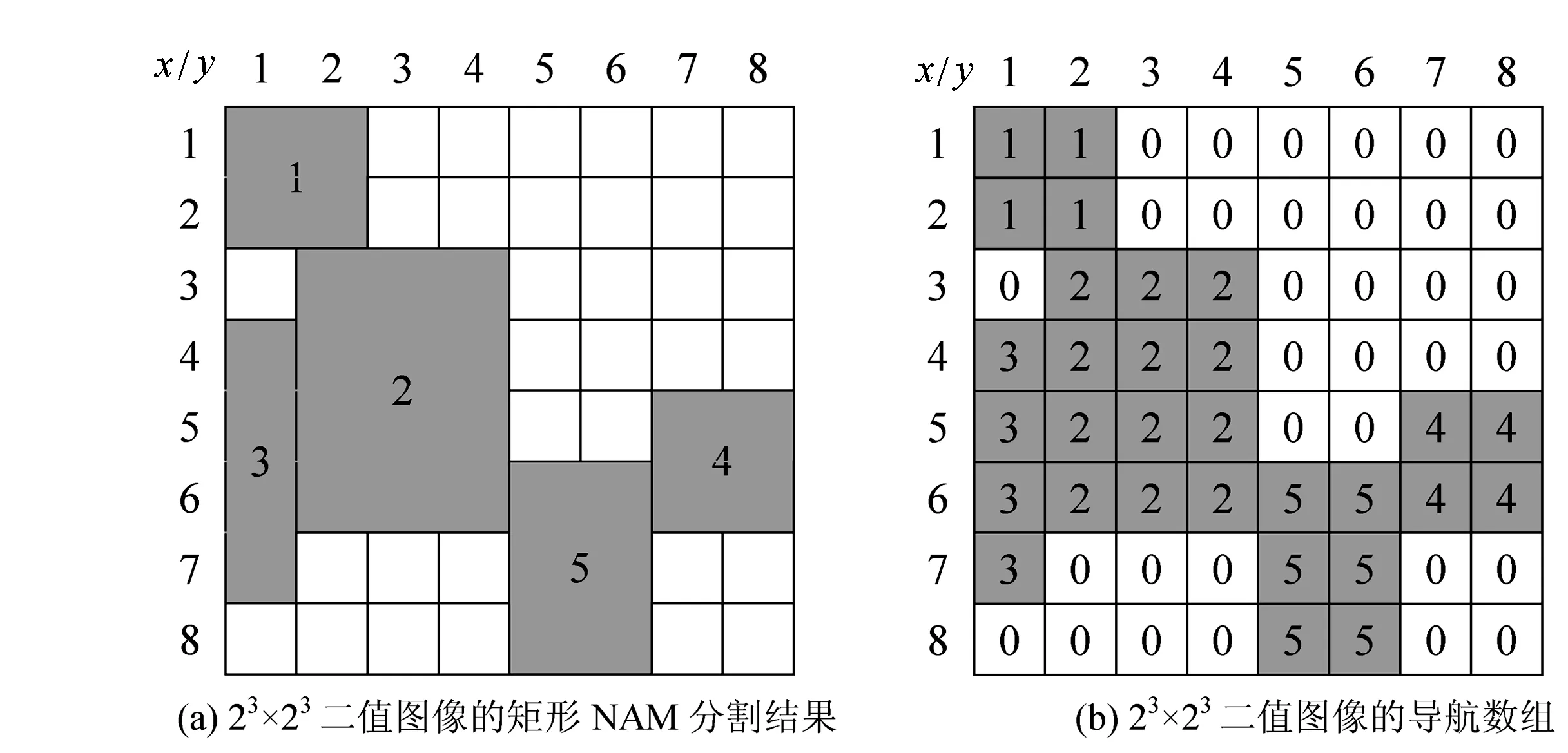
图1 二值图像矩形NAM分割结果及其导航数组
在基于NAM的图像集合运算中,经常涉及查找相邻或相交的块等操作,导航数组(Navigation Array)就是为了解决块之间位置关系问题而设计的。图1(a)所示是二值图像的NAM表示示意图,块中的数字表示经过NAM分割所得的编号,图1(b)是相应的导航数组示意图。从图中可以看出,导航数组就是将块中的每个像素单元以块号填充就可以了,其它则以0填充。在进行查找某个块的近邻运算中,只需将该块的周围一圈像素扫描一下,得到的几种编号就是该块的近邻。在分裂组合法中,由于经常要查找一个图像中某个块中另一个图像中相邻或相交的块,其作用就更加明显。导航数组生成时是只需要遍历NAM表,将每个块的编号插入到二维数组的相应位置即可。根据统计,黑白二值图像中黑色点将占一半,因此,对于总像素为NP的图像,其导航数组生成算法的时间复杂度为O(NP)。
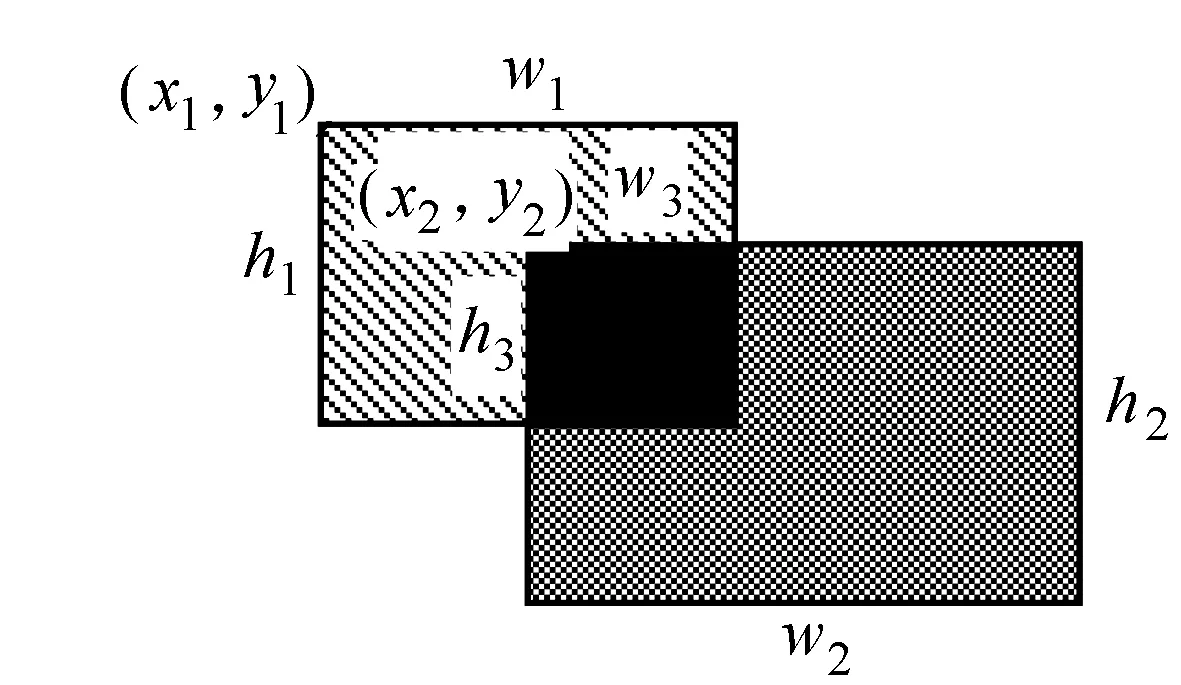
图2 2块相交部分示意图
下面介绍分裂组合法。如图2所示,其中(xi,yi)代表矩形的起点坐标,hi、wi代表矩形的高和宽,2个矩形的相交部分就是图2中的黑色块,设其起点坐标为(x3,y3),高和宽为h3和w3,max和min 分别是:
(x3,y3)=(max(x1,x2),max(y1,y2))
(1)
h3=min(x1+h1,x2+h2)-max(x1,x2)
(2)
w3=min(y1+w1,y2+w2)-max(y1,y2)
(3)
求最大值和最小值函数,于是可以得到式(1)~(3),用来确定相交块的位置及大小,只有当h3和w3均大于零才表示2个块相交,否则表示不相交。
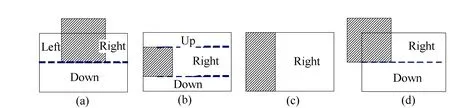
图3 空白块和阴影块分割与标注
在确定了相交部分的位置后,沿相交部分的边将其中一个块的剩余部分分裂成几个子矩形块,选择要保留的部分,最后在所有块分裂结束后,把相邻的块进行组合,这个方法就称为分裂组合法。尽管这种分裂方式有很多种,为了表示的方便,作了一个约束:只添加水平分割线。图3中的虚线就是在这个约束下所加入的分割线。这样分割的好处是可以使得左右2边分割出的矩形与相交部分等高,而上下2边分割出的矩形与空白块等宽,利用所求出的相交部分计算分裂出来的各个块的位置大小就很方便了。在这些分割出的矩形中,还可以分为上、下、左、右4类,分别称为Up块、Down块、Left块和Right块。在图3中,将以上各种情况分割出的矩形作了一下标注。
经过大量的分析研究后发现,NAM表示的图像的集合运算(交、差、并)完全可以通过分裂组合法来完成,其中的关键就是“选择要保留的部分”。比如说,交运算只保留相交部分作为结果,其他部分分裂成新的块,而差运算则是剔除相交部分,将其他部分不断分裂,把最终剩下的块(差运算中要保留的部分)作为结果。以图3(a)为例,假设2个图像中的NAM块分别形成空白块和阴影块2个队列,在求它们的交运算时,依次扫描阴影块队列,利用其导航数组,找到与各个阴影块相交的空白块,在图3(a)的情况下,将一个空白块分裂成3个空白块:Left块、Down块和Right块,将它们加入到空白块队列,并修改导航数组,把相交部分保存到结果队列中,于是一个阴影块处理完毕,再处理下一个阴影块。等所有的阴影块处理完毕,再将结果队列中的块进行优化组合,使最终的块数尽量达到最少。
2 基于NAM的图像集合运算算法
基于NAM的图像集合运算有多种实现的途径,笔者将采用分裂组合法来实现。由于各种集合运算实现上有类似之处,下面仅以交运算为例,给出其详细的算法描述。图像A与图像B的交运算实质上就是在图像A和图像B上查找它们都存在的黑色点,这些黑色点所形成的图像就是它们进行交运算的结果。在该算法中,就是要把所求得的相交部分保留下来即可(Step 2~ Step 9采用了分裂组合法)。
输入:2n×2n的二值图像G1、G2的NAM表NAM1、NAM2。
输出:2n×2n的二值图像G3的NAM表IntersectionNAM。
Step 1 根据NAM1生成对应的导航数组NaviArray;
Step 2 依次循环扫描图像G2中各黑色块,借助导航数组NaviArray分别取出在图像G2黑色块内的编号,如果编号为0,则进入下一轮循环;如果编号不为0,则根据式(1)~(3)求出该编号块与图像G2黑色块的相交部分坐标及大小,将相交部分保存到IntersectionNAM中,并在其导航数组ResultNaviArray中填入相应的编号;
Step 3 计算Up块、Down块的高以及Left块、Right块的宽;
Step 4 如果Up块存在,修改NAM1中编号块的大小即可;
Step 5 如果Down块存在,在NAM1中添加一个等宽的高为Down的新块,并在导航数组中更新新块所在部分的编号;
Step 6 如果Left块存在,在NAM1中添加一个与相交部分等高的宽为Left的新块,并在导航数组中更新新块所在部分的编号;
Step 7 如果Right块存在,在NAM1中添加一个与相交部分等高的宽为Right的新块,并在导航数组中更新新块所在部分的编号;
Step 8 更新NAM1中的总块号,如果G2中黑色块没扫描完,就返回Step 2;
Step 9 依次循环扫描IntersectionNAM中各黑色块,借助其导航数组ResultNaviArray和组合规则判断上下左右4个点,如果左右的块等高或是上下的块等宽,则可将它们组合成一个新的块;
Step 10 去掉IntersectionNAM中高度为0的块并设置块头。
差运算和交运算类似,与之不同的是,在判断出2块相交的情况下,去掉相交部分,而保留其它部分,最后剩下的就是差运算的结果。由于在算法上与交运算几乎相同,为节省篇幅,在此仅说明它们不同的2个地方:①在Step 2中,相交部分不保存;②在Step 9中,把NAM1中的块作为DifferenceNAM,代替IntersectionNAM进行组合优化。并运算可以借助前面2个运算来实现。可以将2个图像的差运算结果与第2个图像的NAM块进行合并,再进行优化组合,就是最终并运算的结果。
下面讨论上述3个集合运算算法的时间复杂度。设整个图像的像素总数为NP,NAM2的结点数为NQ,在3个算法中都调用了生成导航数组的操作,复杂度为O(NP),而在依次扫描NAM2各结点的循环中,复杂度为O(NQ),由于只标注黑色像素块,显然有NPgt;NQ,因此总的算法时间复杂度为O(NP)。
3 试验结果及分析
试验环境为Intel Celeron 1.4GHz移动处理器、512MB内存、Windows XP Professional操作系统、Matlab 6.5编程环境。图4是试验所用的4幅二值图像,大小均为256×256。

图4 试验使用的4幅28×28的二值图像
表1给出了图4所示的4幅数字图像的实验结果,Cp表示图像复杂度,从表中可以看出,实验结果以相应图像的图像复杂度的递增序排列。从表1中可以观察到,随着图像复杂度的增加,线性四元树表示、紧凑四元树表示的节点个数和NAM表示的矩形个数都在增加。对于复杂度较低的图像,NAM表示相对于线性四元树表示、紧凑四元树表示的压缩率一般都很高,它们的比值可以达到4.967,而对于复杂度高的二值图像,NAM表示也不逊色,与其它2种表示的比值也达到了1.204和1.688。从这些数据可知:NAM表示相对于线性四元树表示和紧凑四元树表示需要更少的表示单元数。

表1 线性四元树、紧凑四元树表示与NAM表示的精简性对比

表2 集合运算效率比较
从表2中的结果来看,在测试图像上,基于NAM的集合运算算法比基于紧凑四元树的集合运算算法运行效率都要高,这一点从加速比中表现得相当明显。对于2组图像,集合运算的加速比最低达到1.291,最高达到了5.368。总的来说,由于NAM表上的精简性,使得处理个数上的减少,进而使循环次数减少,因此,在集合运算性能上比紧凑四元树的效率更高。
4 结 语
笔者在非对称逆布局图像表示模型(Non-symmetry Anti-packing Image Representation Model, NAM)的基础上,提出了基于NAM的集合运算算法,并对算法作了复杂性分析。试验结果表明,基于NAM的集合运算算法的执行速度是基于紧凑四元树集合运算算法执行速度的1.291到5.368倍。大量的研究表明,NAM能够有效地减少表示一幅图像所需要的存储空间,是一种良好的图像表示方法。
[1]Hunter G M. Operations on Images Using Quad Trees[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 145~153.
[2]Bauer M A. Set Operation on Linear Quadtrees. Computer Graphic and Image Processing,1985, 29(2): 248~258.
[3]Kawaguchi E, Endo T. On a Method of Binary-Picture Representation and Its Application to Data Compression[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1980, PAMI-2(1): 27~35.
[4]Lin T W.Set Operations on Constant Bit-Length Linear Quadtrees[J]. Pattern Recognition, 1997, 30(7): 1239~1249.
[5]Yuh-Horng Yang, Kuo-Liang Chung, Yao-Hong Tsai. A Compact Improved Quadtree Representation with Image Manipulations[J]. Image and Vision Computing, 2000, 18(3): 223~231.
[6]陈传波, 何大华, 黄文奇.求解单位等边三角形 Packing问题的近似算法[J].计算机学报,2003, 26(2):212~220.
[7]Chen Chuan-bo, He Da-hua. Heuristic Method for Solving Triangle Packing Problem [J]. Journal of Zhejiang University, 2005, 6(6): 565~570.
[8]陈传波. 非对称逆布局模式表示方法研究 [D]. 武汉: 华中科技大学图书馆, 2005.
[9]郑运平, 陈传波. 一种基于NAM的彩色图像表示方法研究 [J]. 软件学报, 2007, 18(11): 2932~2941.
[10]Yunping Zheng, Chuanbo Chen, Mudar Sarem. A novel algorithm for triangle non-symmetry and anti-packing pattern representation model of gray images[J]. Proceedings of the 3rd International Conference on Intelligent Computing (ICIC'07), 2007, LNCS 4681:832~841.
[编辑] 易国华
TP391
A
1673-1409(2009)02-N076-04
2009-03-01
国家高技术研究发展计划(863)资助项目(2006AA04Z211)。
伍鹏(1978-),男,2001年大学毕业,硕士,讲师,现主要从事图像处理与模式识别方面的教学与研究工作。
