基于临界面法的纤绳节点板疲劳损伤评估

谢志英 (长江大学城市建设学院，湖北 荆州 434023)

基于临界面法的纤绳节点板疲劳损伤评估

谢志英 (长江大学城市建设学院，湖北 荆州 434023)

采用基于临界面的多轴疲劳寿命预测方法，对纤绳节点板在长期的风荷载作用下的疲劳损伤进行了评定。以最大剪应变平面的方法确定每一个时间点的临界损伤面，根据非比例多轴加载下最大剪应变临界面不断变化的特点，再以该平面对材料损伤影响的大小为权值进行加权平均，把权值平均最大的剪应变平面定义为临界损伤平面；用多轴循环计数法对临界损伤面上的正剪应力同时进行循环计数，确定每个循环的临界损伤参量。结果表明，临界面法更符合纤绳节点板多轴非比例加载的实际情况，因而可以给出更加合理的结果。

纤绳节点板；多轴非比例加载；损伤参量；临界面法

近几十年来，大量高耸结构特别是桅杆结构疲劳破坏事故频频发生。研究表明，在杆身弦杆及纤绳节点板处最易受到疲劳损伤。纤绳节点板的疲劳破坏的原因是纤绳的微风共振出现频率很高，使纤绳节点板区出现频繁的振荡弯曲应力，最终导致疲劳破坏。传统对疲劳的描述方法是以应力或应变作为力学参量，用它们与循环加载次数的回归关系作为相应的疲劳方程，即以s-n曲线为依据的名义应力法及局部应力应变法。

图1 基于临界面法的疲劳寿命预测步骤

到目前为止，还没有一个普遍令人接受的多轴疲劳寿命预测模型。其主要原因是损伤参量中含有物理意义不明确的材料常数，而这些材料常数有时并不是恒定不变的，从而给寿命估算带来了困难。目前最为普遍接受的方法是临界面法[1～4]，该法将最危险的损伤平面与经受最大法向应变的最大剪切平面结合起来，用其面上的切应变与法向应变构造多轴疲劳损伤参量，进而建立多轴疲劳寿命预测模型。

对于纤绳节点板，在随机风荷载作用下，所受拉力随机变动，采用临界面法能更加恰当的描述其多轴非比例加载的受力状态，从而能够更加准确的估算其疲劳寿命。

1 临界面法的基本原理

首先找出临界损伤平面，然后将其面上的剪切和法向应力(应变)进行各种组合来构造多轴疲劳损伤参量，建立疲劳寿命方程，具体流程如图1所示。

2 纤绳节点板疲劳寿命预测

2.1临界损伤面的确定

1)节点板的局部模型 根据节点板的局部尺寸，通过ANSYS有限元软件,采用SOLID45单元，六面体网格划分单元，耳板材料和杆身材料均为16Mn钢，建立如图2所示的实体模型。

以纤绳的应力作为外荷载，并考虑其角位的变化进行有限元计算，取节点板上危险点在循环载荷作用下在整体坐标系O-X-Y-Z下的应变张量, 计算得到危险点(NODE2572)的正剪应变时程。

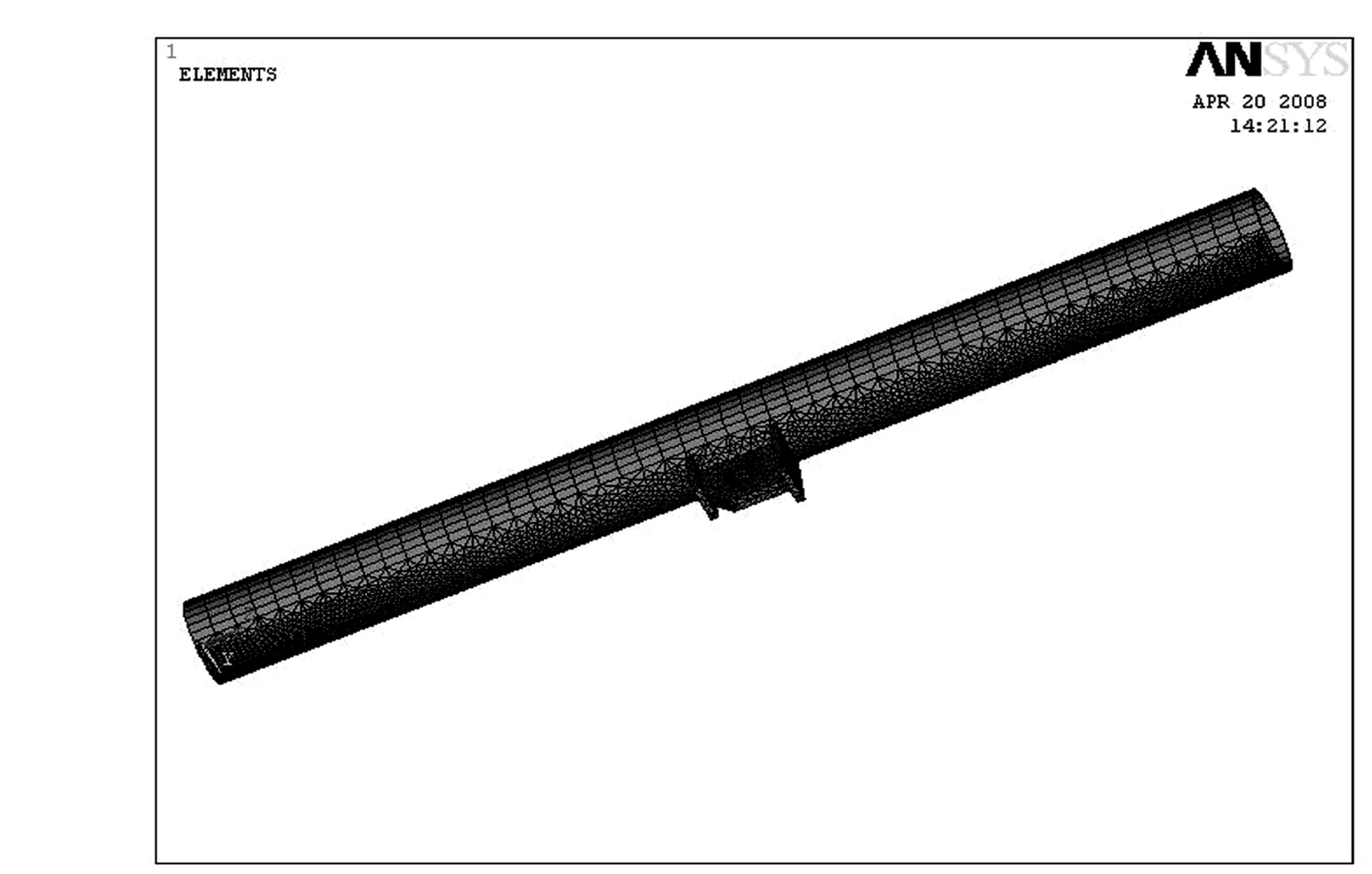
图2 节点板局部实体

2)临界损伤面的确定和计算 临界损伤面即疲劳失效发生在某一特定的平面[5]，疲劳损伤的累积、寿命估算都在该平面上。而疲劳裂纹通常萌生于滑移带的局部塑性变形区，已有的试验结果证明，这些滑移带的滑移方向与最大剪应变的方向非常接近，并且在不同载荷情况下，疲劳裂纹通常都萌生于最大剪应变平面[6]，基于此，选取通常采用的确定临界面的方法——最大剪切平面为临界损伤面，即首先求出每一时刻的最大剪应变平面，作为这一时刻的损伤临界面。根据非比例多轴加载下最大剪应变临界面不断变化的特点，把权值平均最大剪应变平面定义为临界损伤平面[7,8]:

(1)

式中，θr(ti)、Φr(ti)为每一时刻的临界损伤面所对应的角度；w(ti)为θr(ti)、Φr(ti)的权值，与该平面对材料损伤影响的大小有关。

2.2多轴循环计数

多轴应力时间历程的应力循环计数算法是多轴疲劳寿命预测的关键技术之一。对于非比例加载，临界面上剪应变和正应变历史存在相位差，峰谷值不同时出现，因此，需要多轴载荷压缩处理和循环计数方法[9]。

1)峰谷值检测 多轴加载的峰谷值的取舍要保持同步性,即只要临界平面上剪应变和正应变随机载荷序列中的对应点有一方是峰谷值就被提取。图3和图4所示分别为经数据压缩之后的临界面上的正剪应变时程曲线，上层耳板有峰谷值点94个，下层耳板有峰谷值点95个。

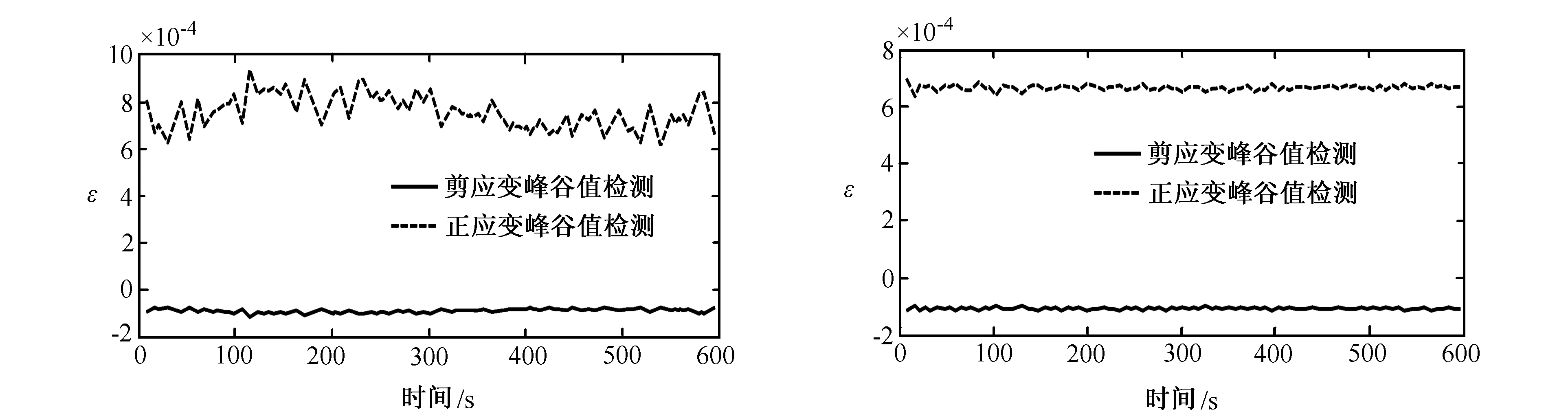
图3 上层节点板峰谷值检测的正剪应变时程曲线 图4 下层节点板峰谷值检测的正剪应变时程曲线

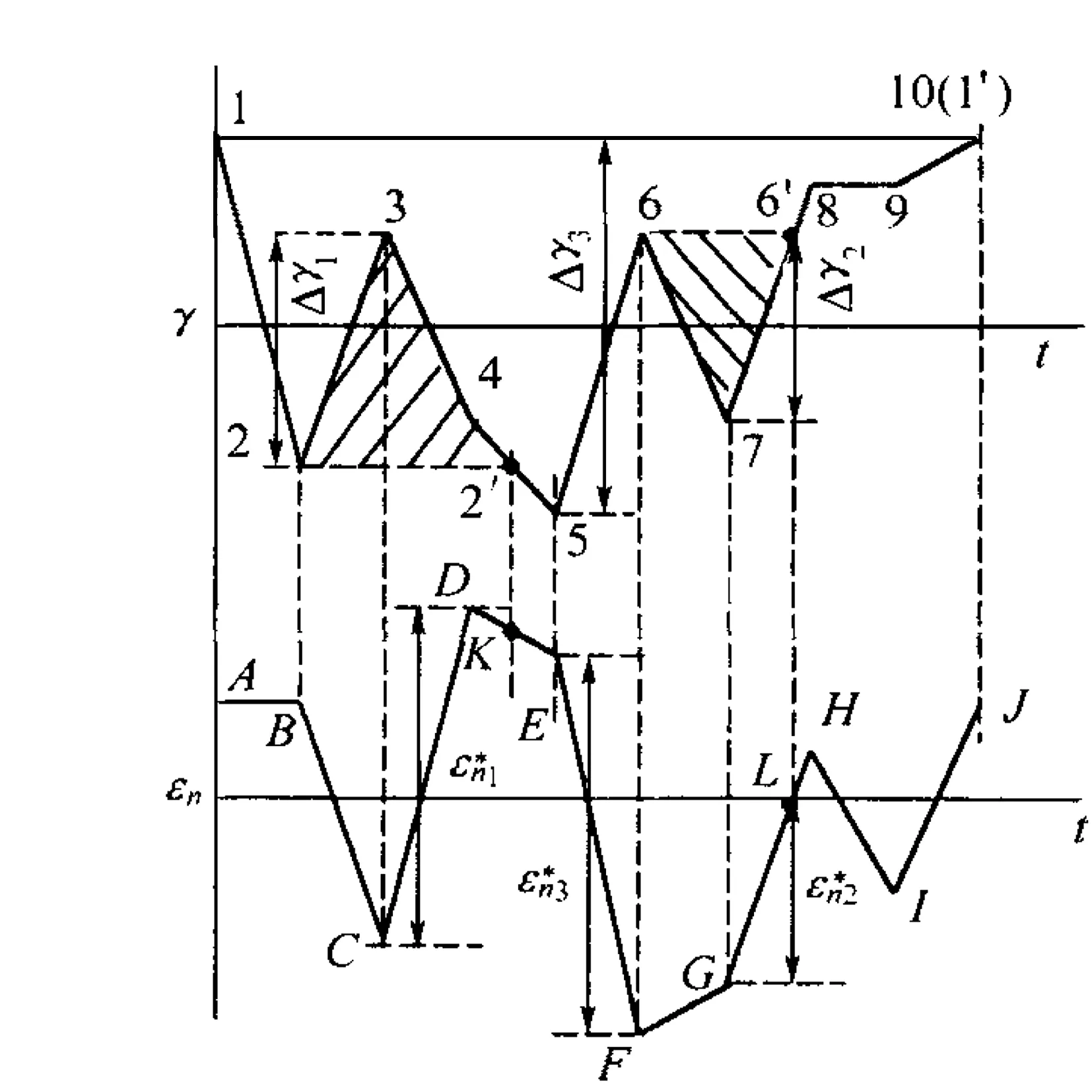
图5 多轴循环计数

2)循环数提取 材料损伤是由于滑移面上沿滑移方向上的切应力达到临界值发生滑移,从而产生驻留滑移带造成的,所以剪应变是控制疲劳损伤的重要参数。同时因疲劳裂纹是由于沿裂纹尖端剪切带的聚合过程而扩展的,它会因正应变的存在而加速[10],所以可以首先对临界平面上剪应变历史进行雨流计数,得到剪应变的全循环和折返点信息,然后提取每个全循环中剪应变折返点对应的正应变最大变程。

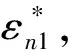
2.3疲劳寿命的估算

1)单个循环的疲劳损伤 Manson-Coffin[9]公式适用于中短寿命区，同时需要作平均应力的修正。通常不做试验难以选择平均应力的修正方法。而Δεeq-N曲线[11]适用于各个寿命区，且不需要作平均应力的修正。但是相对于Manson-Coffin公式，其试验工作量要大一些。

此处采用Δεeq-N曲线的寿命估算模型来计算每个循环的疲劳损伤，即：

(2)

式中，A0、A1为回归常数；εu为对应于1/4循环时的应变，由εu=εeq|N=10+0.0025确定；εe为对应于疲劳极限时的应变，由εe=εeq|N=108+0.0025确定。

2)疲劳损伤累积及寿命预测 虽然节点板是多轴非比例加载的复杂受力状态，但是其随机载荷系列中的疲劳载荷几乎全部处于高周疲劳区，因此，此处仍然可以采用Miner定理[12]进行损伤累积。即：

(3)

式中，Ni为对应于当前载荷水平Si的疲劳寿命；ni为实际的循环次数。破坏准则为D=∑ni/Ni=1。根据Miner线性累积损伤理论，可以得到桅杆结构上下节点板的危险点在0°方向13m/s的风速下60s内的疲劳损伤分别为1.47E-07和4.26E-10。

3 结 论

1)临界面法更加符合纤绳节点板多轴非比例加载的实际情况，因而可以给出更加合理的结果。

2)基于临界面法的节点板疲劳寿命计算主要包括：采用权值平均法进行临界面的确定；用多轴循环计数进行临界面上损伤参数的确定；确定和计算多轴疲劳统一损伤参量。

3)给出了一种多轴载荷处理方法与循环计数方法,该方法实现了多轴载荷的取舍同步性,可以同时得到剪应变和正应变的循环计数结果。

[1]王肇民,桅杆结构[M]. 北京：科学出版社, 1985.

[2]李树逊,王肇民.桅杆结构在模拟风荷载作用下的非线性动力分析[J]. 建筑结构,1999,(2):109～113.

[3]瞿伟廉，李波.桅杆结构风振响应有控制研究综述[J].武汉理工大学学报,2002,(11)：53～56.

[4]王雷,王德俊. 一种随机多轴疲劳的寿命预测方法[J]. 机械强度,2003,(2):204～206.

[5]王之宏，风荷载的模拟研究[J].建筑结构学报，1994，(1):215～219.

[6]U.Pei1, H, Not Ie.On Fatigue of Guyed Masts due to Wind Load[M]. Rotterdam:Structural Safetyamp;Reliability, 1994.

[7]王之宏，桅杆结构的风振疲劳分析[J].特种结构，1994，(3):302～306.

[8]颜明忠，桅杆结构风振动力响应理论及实验研究[D].上海：同济大学，1998.

[9]尚广德，王德俊. 多轴疲劳强度[M]. 北京：科学出版社,2007.

[10]Cartensen H V, Magnin T. Characerization and quantification of multiple crack growth during low cycle faigue[J].International Journal of fatigue,2001,23(1):195～200.

[11]Goto M,David K M. Initation and propagation behavior of microcracks in Ni-base superalloy Udimet[J].Enigineering Fracture Mechanics,1998,60(1):1～18.

[12]屠海明，桅杆结构风振疲劳分析[D].上海:同济大学，2000.

[编辑] 李启栋

TU312+.3

A

1673-1409(2009)01-N105-03

2008-12-23

谢志英(1966-)，女，1988年大学毕业，硕士，高级工程师，现主要从事土木工程方面的教学与研究工作。