统计过程控制用于教学过程改进

任爱华

摘要:教学质量与产品质量的要求特点不同。因为教学的对象是人,它包含了教师“教”以及学生“学”的质量问题,其质量的实现,显然与人的因素具有非常密切的关系,比起物质产品的质量,自然要复杂的多。如何科学地衡量教师的教学质量与学生的学习质量,一直是教学探索的主题。本文论述了我院针对学生课堂出席率的统计数据,结合课堂问题反馈,利用控制图反映教学过程的异常情况,并通过统计过程控制稳定改进教学过程,这一方法为量化教学质量奠定了基础。

关键词:教学质量;统计过程;量化;控制图

中图分类号:G642 文献标识码:B

1引言

教学质量是学校生存与发展的生命线。学生评教是整个教学过程中实现学校教学质量自我监控的重要环节之一。学生是老师教学的对象,是教学质量好与差的直接接受者,学生有权力和义务也有条件对教师的教学工作进行评价。通过学生对教师教学工作的评价,能进一步增进师生之间的沟通与了解,促使教师更加关注学生,不断更新教学观念,改进教学方法,提高教学质量。另外,学生评教的结果还是学校加强和改进教学管理工作的重要依据,在提高教学质量中起着非常重要的作用。

如果把老师看成是生产人员,而掌握了知识的学生则是产品。学生既然具有可塑性,老师就该从教学内容的组织、教学方式、课外辅导、作业批改各方面采取措施,以优质教学来对每一个学生负责,而这一系列的环节形成了教学过程。如果对教学过程的每个环节都进行了详细周到的安排,并付诸实施,那么教学质量就会得到保证。良好的生产过程必然会导致优质的产品,这在制造业、软件行业等众多领域已经得到了证实。

作为授课的教师可以通过采集学生的听课出席情况数据统计了解教学过程性能以及教学过程中所存在的问题。通过这些统计数据了解自己的教学水平和执教能力,可以根据过程数据的反馈情况及时调整教学环节与方法,

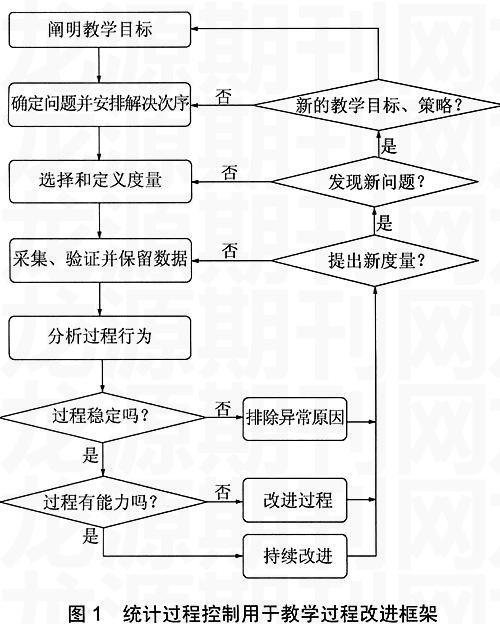
本文提出了通过量化指标改进教学过程的流程,如图1所示。通过这个流程,实施教学过程的改进,从而保证教学质量。

在图1中,首先要提出教学目标,然后将其落实到教学过程中的度量目标,针对度量目标确定度量元并采集度量结果,通过这些采集到的数据反映教学过程的异常情况和教学过程的稳定性,从而决定教学过程改进的具体措施。过程改进需要持续进行、不断改进,这样才能不断提高教学水平,图1的过程改进框架表达了这一规律。

统计过程控制(SPC)及其相关的控制图是由Walter A.Shewhart在20世纪二十年代提出,用于对产品成本和质量的控制领域。Shewhart的技术在第二次世界大战中得到广泛应用,并且在近些年被W.Edwards Deming等人作为改进产品质量的基础,在日本和很多美国的企业中重新得到推广。由于SPC在工业界中获得巨大成功,这种技术已经被应用到很多其他商业领域、服务业和软件界的过程改进。

本文将采用XmR控制图了解和分析学生听课过程的稳定性,通过采集这方面的数据对听课过程进行统计过程控制,发现学生听课过程中存在的异常,解决异常,稳定过程,并改进教学过程,提高过程能力,为高质量的教学过程奠定量化基础。

2量化教学过程

量化教学过程首先是在提出了教学目标的基础上,确定度量目标,而由度量目标决定具体的度量元,通过对度量元的采集,最终形成教学评价需要的指示器。学校每个学期都有针对教师讲课情况的听课记录,通常的格式如表1所示。

在表1中,内容有定量与定性两类评价。其中的“人数”一栏填写每次听课学生数目,如果以每次课记录的人数为采集的基础数据,当累计几次课的数据之后,将这些数据绘制到控制图上,便可以从控制图中观察出当前学生听课过程的性能,以此反映教师执教的能力。通过这些过程数据,可以让教学过程表达自身的性能和异常点,随着累积数据的增多,过程的状态会更加真实地展现在控制图上。

采集每次听课人数,可以采用两种途径。一种是通过旁听课程的教师客观地记录,以此形成的控制图曲线可以反映学生平常听课的状态和教学质量。另一种是通过授课教师每次上课前提供签到表,统计听课人数。这种方式会对学生有触动,因为大部分学生都会担心自己的缺课可能给授课教师留下不良印象,因而会有较多的人签到听课。授课教师自己采集听课人数的方式实际上加强了教师与学生之间的互动和交流,以签到的形式既可督促学生主动参与正规课堂教学的学习,又可从采集的这些数据中展示目前学生“听课过程”的性能和存在的异常情况。授课教师可以根据这个性能曲线确定问题,了解听课的稳定情况,及时解决问题,从而控制教学过程并使之得到改进。

控制图是量化过程行为的技术。控制图以及统计质量控制相关方法若用在为实现目标而执行的活动的上最有效。

本文旨在保证教学质量,首先要稳定教学过程,再经过不断地改进教学过程,提高教学水平。这一过程非常适合统计过程控制,即让数据说话,使教学过程可视化,从中发现教学环节中的问题,通过解决问题不断地改进教学过程,从而可以预测过程性能并保证高质量的教学。

3利用控制图揭示教学过程中的异常环节

3.1控制图基本要素

所有传统的控制图都有一条中心线并在中心线的两侧有控制限。中心线和上下控制界限都是在执行过程时采集的一组观察值经统计公式计算得出的估计值。中心线和控制限是不能擅自假设的,因为要用这三条线揭示过程实际能做什么,即表达过程现有的性能水平,而不是通过这三条线要求过程去做什么。

画在控制图上的值是从任意特定的度量统计中得到的观察值,像分组平均值、分组值域、移动平均值、移动值域、以及单点值本身都是可以按时序绘制在控制图上的统计例子,成为控制图的基础。

控制图的基本形式如图2所示。中线通常是被观察过程的平均值。在中线两侧的上下控制限是从过程可变性度量导出(最常出现的分组值域)。传统的(Shewhart)控制限是±3σ,这里σ是画在图上的偏差统计。如果一个控制限超出了值域的可能结果,比如一个负值的产品尺寸,通常则省略这种控制限。

本文采用单点图和移动值域图(XmR-图)来检查过程数据的时序行为。表2提供了构造XmR-图的基本要素的实例,即:通过学生听课出席数据反映教学过程稳定性。利用表2中的数据绘制的控制图如图3所示。

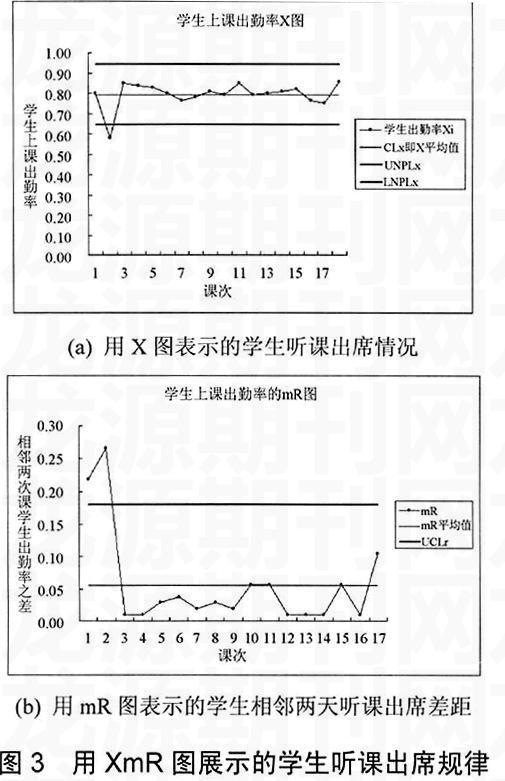
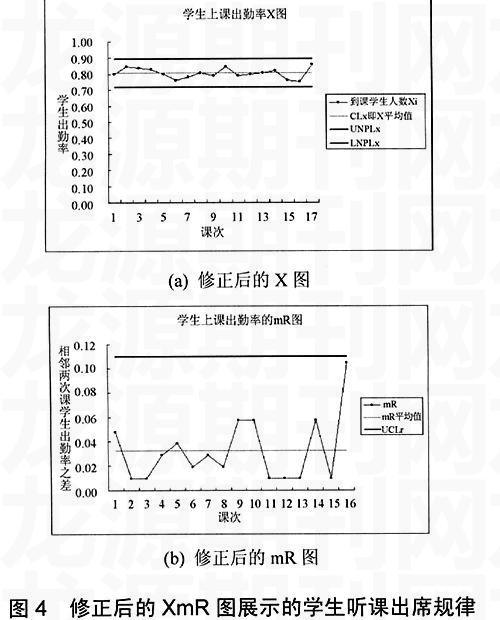
在图3(a)中较早地出现了一个偏差,即:第二个值过低,超出了控制下线。根据稳定过程的定义可知,这个过程不是一个稳定过程。通过对该数据的调查,发现是由于另一门课程的大作业到了提交期限,这部分同学为了突击这个上机作业造成缺课。当解决这个问题之后,将该数据剔出,重新计算控制线,得到的结果如图4所示。这时的控制图展现出一个稳定过程。

3.2教学过程的性能分析

从图3到图4可以看出,当排除了这个异常因素之后,根据控制图分析理论,图4呈现的听课过程是稳定的,学生的出席率在81%左右。从学生的听课出席率可以反映出该过程的能力,也就是说,如果保持目前的授课方式不变,学生听课率会一直维持在81%左右。图4揭示出这是一个稳定过程,如果希望提高听课率,则需要改进授课环节。

3.3建立过程性能模型

当得到了一个稳定的过程之后,可以根据学生听课出席率与学生作业出错率两类数据,分析两者之间的相关性,根据表2数据可得出:这两组数据之间具有0.99相关性,通过回归分析,可以得出预测模型为:

Y=0.83-0.82X

其中:X为学生听课出席率;

Y为学生作业的出错率。

利用该过程性能模型,可以根据学生出席率预测学生作业的完成质量。比如:当学生听课率为90%时,可以预测学生的作业总体出错率约为9%。

4教学过程的改进

由于在图3(a)中展示了学生听课过程存在异常原因,通过对异常原因的调查之后,解决了存在的问题并在今后的教学中避免出现类似的问题,从而可以保证教学过程的稳定性。对于一个稳定的过程,可以预测结果,此时的XmR图上下控制线和中线代表了该过程的能力。学生的听课率的高低反映了学生对该课程的认可程度,在上述例子中,平均听课率为81%,它反映了绝大部分同学对本课程的认可程度,但仍然有个别同学没有经常出席,利用过程模型预测一下学生作业出错率,其值接近17%。针对这种情况,可以对经常缺席的同学进行调查了解,寻找解决的办法,进一步采集同学对教学内容的需求。

XmR控制图的三条基线可以揭示学生听课的稳定性和教学环节存在的异常点,当教学过程稳定之后,可以通过XmR图展示的过程能力,了解与教学目标要求的能力之间的差距。在教学过程改进中,可以根据紧迫程度,有目的地选择某个教学环节进行改进,逐步提高能力水平。比如教师授课水平、课程内容的实用性、与其他课程的衔接性等。总之,需要对教学过程涉及到的各种环节进行调查了解,找到根本原因,对症下药,提高学生的听课率,保证高质量的教学。教学过程的改进是多个环节相互协调和配合的活动,比如:教师专业素质、授课经验和水平、讲课环境与设施、配套教材和实验环境等。这些都是影响着优质教学的因素,需要得到保障,而这些环节同样可以作为过程的因子确定度量元,选择合适的度量元并对其进行采集、分析,依据这些度量数据了解教学过程相应环节的稳定性。在此基础上,再从反映学生的学习效果的因变量上进行度量,观察这些度量数据的相关性,从而可以得出这些过程因子的稳定性对学习效果的影响。如果相关性很高,则可建立过程性能模型,通过调整过程因子便可以使得因变量“学习效果”得到改善。此项工作需要长期的数据积累,持续的过程进行改进。

5结束语

统计过程控制可以用于教学过程改进。通过量化教学过程,展现教学过程中存在的异常情况,通过对异常情况的调查和了解,可以排除造成过程异常的特殊原因,从而使教学过程逐步达到稳定状态。在此基础上利用控制图可以进一步了解教学过程本身的能力,将其与教学目标进行比较,看看是否达到了要求。若没达到则需要在教学过程的各种环节上进行分析,找出影响教学过程能力的根本原因,确定教学过程的关键环节,再针对这些关键环节开始新一轮的教学过程改进,从而提高教学水平。过程改进是一个持续不断的过程,只有持续进行,才能保证质量,达到预定的目标。

参考文献:

[1] William A. Florac, Anita D. Carleton. Measuring the Software Process[M] .New York: ADDISION-WESLEY,1999.

[2] Shewhart Walter A.. Economic Control of Quality of Manufactured Product[M]. New York: Van Nostrand, 1931.

[3] Deming W. Edwards. On Probability as a Basis for Action[J]. The American Statistician 29, no. 4(1975):146-152.

[4] Austing Robert D.. Measuring and Managing Performance in Organizations[M]. New York: Dorset House Publishing Company,1996.

[5] Wheeler Donald J.. Understanding Variation-The Key to Managing Chaos[M]. 2nd ed. Knoxville, Tenn.: SPC Press, 2000.

[6] Wheeler Donald J., Poling Sheila R.. Building Continual Improvement[M]. Knoxville, Tenn.: SPC Press,1998.

[7] 李菊华,同毓舟. 六西格玛工具手册[M]. 上海:上海交通大学出版社,2005.