基于ＭＡＴＬＡＢ的电路分析教学探索与实践

张思扬　匡芳君

[摘要]引入MATLAB工具进行电路分析教学探索与实践,有利于使复杂电路的分析和计算变得非常快捷、方便,从而为电路分析提供一个有效的辅助工具。

[关键词]MATLAB 电路分析 仿真

中图分类号:G71文献标识码:A文章编号:1671-7597(2009)0910193-02

在电路分析中,随着电路规模的加大,微分方程阶数以及联立方程的个数增多,给解题运算带来一定困难。而MATLABA提供了高效简洁的编程方法,其强大而简易的绘图功能、矩阵和数组运算能力以及很强的扩充性,能充分满足基本电路分析、计算的需要,从而可以大大提高计算精度和工作效率,在电路分析研究与工程实践中具有良好的应用价值。本文仅以一些典型电路为例,研究MATLAB在电路分析中的具体应用。

一、MATLAB在直流稳态电路的应用

例1:如图1所示的电路中,已知C1=0.5F,R2=R3=2Ω,L4=1H;Us=10+10cost,Is(t)=5+5cos2t,求b,d两点之间的电压U(t)。

MATLAB程序源代码:

% program daiweinan.m

Clear,format compact

% 置频率及相应的电压、电流数组、各阻抗数组

w=[eps,1,2];us=[10,10,0];Is=[5,0,5];

z1=1/(0.5*w*j); z2=[2,2,2]; z3=[2,2,2]; z4=1*w*j;

uoc=(z2/(z1+z2)-z4/(z3+z4))*us; % 求开路电压

zeq=z3*z4/(z3+z4)+z1*z2/(z1+z2); % 求等效内阻

u=Is.*zeq+uoc; % 按等效电路求u

disp(' w umphi') % 显示各分量的值

disp([w',abs(u'),angle(u')*180/pi])

程序运行结果:

wumphi

0.0000 10.00000

1.00003.1623-18.4349

2.00007.0711 -8.1301

由此可以写出U(t)的表示式:U(t)=10+3.1623cos(t-18.4349)+7.071

1cos(2t-8.1301)

二、MATLAB在直流暂态电路的应用

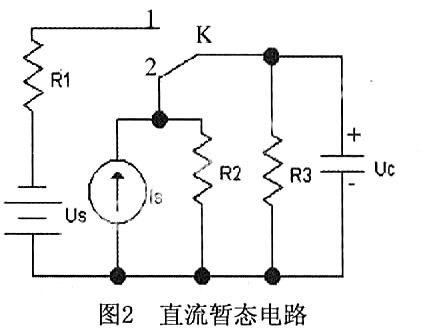
例2:如图2所示的电路,已知R1=3Ω,R2=12Ω,R3=6Ω,C=1F,Is=3A,Us=18V,C=1F。在t<0时,开关K位于1,电路处于稳态,在t=0时,开关K闭合到2,求Uc和IR2的响应,画出它们的波形。

MATLAB程序源代码:

% program zhiliuzhantai.m

r1=3;us=18;is=3;r2=12;r3=6;C=1; % 给出原始数据

uc0=-12;ir20=uc0/r2;ir30=uc0/r3; % 算出初值

ic0=is-ir20-ir30;ir2f=is*r3/(r2+r3); % 算出终值

ir3f=is*r2/(r2+r3);ucf=ir2f*r2;icf=0;

T=[[-2:0]-eps,0:15];% 注意时间数组的设置,在t=0附近设两个点

uc(1:3)=-12;ir2(1:3)=is;% t<0时的值

T=r2*r3/(r2+r3)*C; % 求充电时常数

uc(4:19)=ucf+(uc0-ucf)*exp(-t(4:19)/T);

ir2(4:19)=ir2f+(ir20-ir2f)*exp(-t(4:19)/T);% 用三要素法求输出

subplot(2,1,1);h1=plot(t,uc), grid,set(h1,'linewidth',2)% 绘uc图并加大线宽

text(-2,15,'uc'),subplot(2,1,2),h2=plot(t,ir2); % 绘ir2图

grid,set(h2,'linewidth',2)

text(-2,2.5,'ir2')% 标注

set(gcf,'color','w') % 置图形背景色为白色

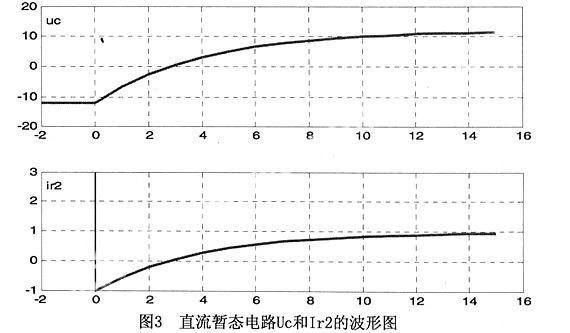
程序运行结果见图3:

三、MATLAB在交流稳态电路的应用

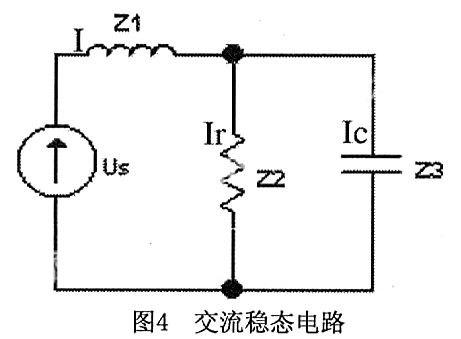
例3:在图4所示的电路中,R=5Ω,ωL=3Ω,1/ωC=5Ω,Uc=10∠300,求Ir,Ic,I和UL,Us。并画出其相量图。

MATLAB程序源代码:

% program jiaoliuwentai.m

z1=3*j;z2=5;z3=-2j;uc=10*exp(30j*pi/180);

z23=z2*z3/(z2+z3);z=z1+z23; % 交流电路方程

Ir=uc/z2,Ic=uc/z3,I=Ic+Ir,uL=I*z1,us=I*z

disp(' uc IrIc I uL us')

disp('幅值'),disp(abs([uc,Ir,Ic,I,uL,us]))

disp('相角'),disp(angle([uc,Ir,Ic,I,uL,us])*180/pi)

ha=compass([uc,Ir,Ic,I,uL,us]);

Set(ha,'linewidth',3)

程序运行结果见图5:

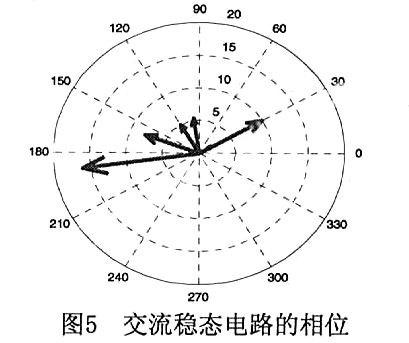
uc Ir IcI uL us

幅值10.00002.00005.0000 5.385216.1555 7.8102

相角30.000030.0000120.000098.1986-171.8014159.8056

四、结束语

本文通过电路分析中的典型例题介绍了如何应用MATLAB软件编程对复杂电路进行分析和计算。实践表明,在电路分析中引入MATLAB不仅可以节约计算时间、方便调试电路参数,而且可以直观地测量电路中电压、电流和功率等物理量,从而大大提高计算精度,缩短编程时间,提高工作效率。

参考文献:

[1]陈怀琛、吴大正、高西全,MATLAB及在电子信息课程中的应用[M].北京:电子工业出版社,2006.

[2]王洪元,MATLAB语言及其在电子信息工程中的应用[M].北京:清华大学出版社,2004.

[3]丁卫民,MATLAB在电类课程中的应用[J].科技情报开发与经济,2007(18):256-258.

作者简介:

张思扬(1973-),男,湖南衡阳人,湖南安全技术职业学院电子信息工程系,讲师,硕士研究生,从事电工电子学方面的教学与研究。