一个融入实例与游戏的教学过程设计

解　辉

摘要 在总结以前教学经验基础上,结合二叉树性质的实际教学需求,设计“理论讲解——实例对照讲解——游戏化理解与加深”的3步教学过程。通过实际的教学运用,证明该过程能够满足不同学习水平的学生理解和掌握该部分知识的要求,达到较好的教学效果。

关键词 教学过程;实例;游戏;二叉树

中图分类号:G642.1 文献标识码:B 文章编号:1671-489X(2009)21-0030-02

Design for Teaching Process with Case and Game//Xie Hui

Abstract Based on prior teaching experience summary and combined with the binary tree teaching function needs, designed theory explain, examples contrast explain, the game of understanding and deepening, all the teaching process in 3 steps. Using this methods in teaching process, we prove that the process can meet the needs of different levels of students to understand and acquire this part of knowledge, to achieve better teaching results.

Key words teaching process; case; game; binary tree

Authors address Computer Department of Qinghai University, Xining, 810016, China

数据结构课程是高等院校计算机类专业学习的一门重要专业基础课,而二叉树是该门课程中非常重要的组成部分[1-5]。在讲解二叉树的一些性质时如果学生没能取得很好的理解和掌握,将会对后续内容的学习有很大的影响。

比如在讲解二叉树的性质“对任何一棵二叉树,叶结点个数n0,度为2的结点个数n2,则n0=n2+1”时,传统过程为:“二叉树的叶子数目为n0,度为2的节点数为n2,度为1的节点数为n1,那么该树的节点数为n0+n1+n2;而树中有边n1+n2,这样树的总结点数又可表示为n1+n2+1;那么由n0+n1+n2=n1+2n2+1可推导出n0=n2+1或n2=n0-1的公式。”

这个数学推导过程很简单,但是对学生理解不是太直观,很难把n0和n2之间的逻辑关系形象化,更难把n0,n1和n2三者之间的逻辑关系形象化,经常发现学生有这样的疑惑:为什么n0和n2之间就成了n2=n0-1或n0=n2+1的关系呢?虽然知道数学推导出来的公式没有错,但就是对它们之间这种数学关系的理解不是很明了、很直观。而在逻辑性较强的理工科课程中,迷惑容易导致连锁反映,容易打击学生的积极性,影响后续的教学效果。相对这些学生,真正的教学目标没有达到[4,6]。

关于数据结构教学,很多同行也结合实际做了相应的研究[3-5]。那么到底怎么样讲解可以使得学生容易接受并在脑子中有一个形象化、直观化的印象和理解呢?其实理论若能与形象化的生活实例结合,往往可以收到良好的效果。尤其若能再融入一些游戏化的环节,则可以达到事半功倍的效果。在总结以前上课经验的基础上,设计“理论讲解——实例对照讲解——游戏化理解与加深”3步教学过程,基本能满足不同学习水平学生的学习要求,达到较好的教学目标。

1 理论讲解:生产消费的过程

1.1 介绍该性质,用传统的方式进行公式推导

1.2 比喻形式的理论过程讲解讲解过程可以引入这样的生产与消费比喻形式:每个结点有0、1或2个子树,有子树则必有对应的“边”,称该结点生产了“边”,有几个子树则生产几条边;除根节点外,其他每个结点都有父节点,也有对应的“边”与父节点相连,称该结点消费了1条边。

那么从总体生产消费的角度看,在任意一个二叉树中,边的生产:总计n0个度为0的叶子结点生产了0条边,总计n1个度为1的结点生产了n1条边,总计n2个度为2的结点生产了2*n2条边,全部所有结点总计生产边数为0+n1+2*n2。边的消费:所有n0+n1+n2个结点中的每个非根结点都需要消费1条边,这样除根节点外总共需要消费n0+n1+n2-1条边。由于整个树中的每条边都会连接一个父节点和子节点,即边的生产量与消费量是相等的,即0+n1+2*n2=n0+n1+n2-1,亦即有n0=n2+1成立。

从每个结点的生产和消费量来看,在任意一个二叉树中,由于根节点(不管其度为几)不消费边,等价于其为整个树多贡献了1条边;度为的0的结点(除根节点外)生产0条边,消耗1条边,边的贡献为-1;度为1的结点(除根节点外)生产1条边,消费1条边,边的贡献数记为0;度为2的结点(除根节点外)生产2条边,消费1条边,边的贡献数记为1。这样就可以看做度为0的结点所需边是由根结点和度为2的边来提供的,因为边的生产与消费是平衡的,即n0=n2+1。

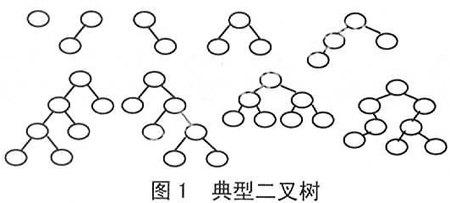
1.3 结合图例的验证图1画出典型的一些二叉树,让学生按照二叉树定义,根节点、叶子节点、度为2的节点、度为1的节点等概念,从各典型二叉树中找出相应的节点数目和边的数目,并分别用n0记录叶子数目,n2记录度为2的节点数,n1记录度为1的节点数,验证一下公式n0=n2+1或n2=n0-1是否成立。同时也可以按照消费生成比喻进行验证。

2 实例对比讲解举例(实例问题驱动的手段)

为了让学生能够进一步明白二叉树的这个性质,可以在上述的理论讲解后引入实例进行对比讲解。

假设你是公司的CEO,你的目的就是为了不断扩大公司的经营范围和实力从而赚更多的钱,扩大公司实力的一个途径就是根据业务需要注册自己的子公司(子公司也可以注册它自己的子公司),但是政府规定每个公司(包括子公司)最多可以从商业管理部门申请到2张licence,并立即利用每张licence注册一个子公司。当然,若每个公司(包括子公司)根据业务可以申请注册2个或一个子公司,也可以不申请注册子公司。为了管理方便,将拥有2个子公司的母公司归类为集团级公司,拥有一个子公司的母公司归类为骨干级公司,没有任何子公司的公司划归为业务级公司。另外,为了区别初始公司(即刚开始担任CEO时那唯一的公司)与后续所有子公司,将初始公司叫做总部公司,并且总部公司在担任CEO之时已经存在,不需要申请licence注册。作为管理者,你在某次年终统计时,统计到公司目前已经拓展到n2个集团级公司,n1个骨干级公司,那么业务级公司的数量n0是否能够算出来呢?所有公司的总数n和3种级别公司各自的总数目之间有什么样的关系呢?

在分析这些不同级别公司之间的数目关系时,有一个很重要的线索就是licence,它是连接子母公司的桥梁。仔细分析会发现,任何一个子公司的产生都需要一个licence,也就是说每个子公司会“消费”一个licence;另外,任何一个集团级公司(不包括总部公司)也会“生产”出2个licence,任何一个骨干公司会“生产”出1个licence,业务公司“生产”0个licence。从生产与消费licence的角度看,该问题的实质其实就与第一部分的比喻形式的理论过程讲解内容一样,也会很自然得到集团级数目与业务级公司数目间的关系:n2+1=n0。

3 游戏化的理解和加深过程

为了让学生对该性质有更加深刻的理解和体会,设计如图2所示名为“找朋友”的课堂互动游戏。游戏中你自己找到的朋友称为“新朋友”,对你的“新朋友”来讲,你是他的“老朋友”。图中的是一条带子,白色端系在“老朋友”身上,黑色端系在“新朋友”身上。

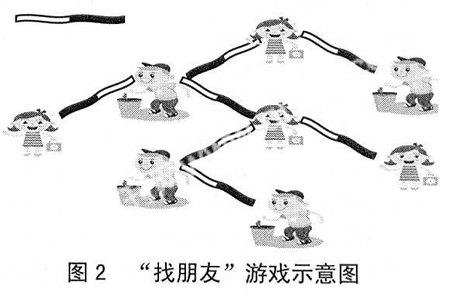
规则:1)每个人只能找0、1或2个“新朋友”,找到后按照带子的颜色端要求系在新老朋友身上;2)自己只能在被某个“老朋友”找到后才能再去找自己“新朋友”,但不能找任何一个有“老朋友”或“新朋友”的同学做朋友;3)游戏只能由一个学生发起,该学生没有“老朋友”,直接开始找他的“新朋友”。

游戏结束时,让大家看看有0个“新朋友”的学生数目n0,1个“新朋友”的学生数目n1,2个“新朋友”的学生数目n2之间的关系,再结合前面2个教学步骤中生产消费的比喻,看看黑白带子与n0、n1和n2间的关系,这些关系是否验证了n0=n2+1。

通过该游戏不仅可以加深学生的知识理解和印象,还能起到调节课堂气氛,增加学习兴趣的效果。结合课堂实际,有时把游戏部分放在课堂开始部分会有更好的效果。

把上述3步教学过程用于实际教学后总体上取得很好的教学效果。同时在教学过程中根据实际教学需求,可以适当地舍取实例讲解或游戏化步骤,也可以调整这2个步骤在整个教学过程中的顺序位置。总之,本文所述将实例与游戏化的思维融入二叉树性质的教学过程设计,不仅有效改善了该节内容的教学效果,而且对其他章节乃至其他课程的教学过程都有一定的参考价值。

参考文献

[1]殷人昆.数据结构(用面向对象方法与C++语言描述)[M].第2版.北京:清华大学出版社,2008

[2]张铭.数据结构与算法[M].北京:高等教育出版社,2008

[3]徐晓伟.《数据结构》教学方法的探索与实践[J].科技信息:学术版,2008(28)

[4]热孜万古丽·夏米西丁.《数据结构》教学方法浅谈[J].科技信息:科学·教研,2008(35)

[5]陈锦涛.电网监控专业《数据结构》课程教学方法探索[J].中国电力教育,2008(20)

[6]禹明秋.学与教的心理[M].北京:高等教育出版社,2004