反倾层状岩质边坡倾倒变形破坏机理综述

邹丽芳,徐卫亚,宁宇,郑文棠(河海大学a.岩土力学与堤坝工程教育部重点实验室;b.岩土工程研究所,南京210098)

反倾层状岩质边坡倾倒变形破坏机理综述

邹丽芳a,b,徐卫亚a,b,宁宇a,b,郑文棠a,b
(河海大学a.岩土力学与堤坝工程教育部重点实验室;b.岩土工程研究所,南京210098)

倾倒变形破坏常见于层状岩质边坡工程,其机理研究对边坡稳定性分析具有重大意义。在国内外相关研究基础上对弯曲倾倒、块状倾倒及块状-弯曲倾倒3种不同破坏模式进行了分析,就边坡几何形状、岩层强度和长细比、层面力学参数、地下水、开挖作用等因素对倾倒变形的影响进行了阐述,介绍了倾倒变形破坏机理在物理模型试验、极限平衡、数值模拟3种方法中的研究进展,指出了不同方法的适用性和优缺点,说明了研究中需要改进和深化的内容。

倾倒变形;破坏机理;层状边坡;数值模拟

倾倒是指层状反坡向结构及部分陡倾角顺层边坡的表部岩层因蠕动变形而向临空方向一侧产生弯曲、折断,形成所谓点头哈腰的现象[1]。倾倒破坏是层状岩质边坡变形破坏的一种典型形式,主要包括弯曲倾倒、块状倾倒、块状-弯曲倾倒3种破坏模式。尽管通常情况下,变形不至于引起坡体的快速变形滑动,但若不加控制的话,仍然可能导致大范围的裂隙发育岩体产生拉裂隙、崩塌等不同形式的破坏甚至深层滑坡[2,3]。

倾倒变形常见于我国的矿山和水电工程中,如西部金川露天矿边坡[4]、锦屏一级水电站左岸边坡[5,6]、小湾水电站饮水沟边坡[7]、昌马水库倾倒变形边坡[8]、龙滩水电站左岸边坡[9]、五强溪水电站杨五庙坝址左岸边坡[10]、小浪底工程库区岸坡[11]、洼里滑坡[12]等。鉴于倾倒变形的复杂性和在边坡工程中的重要性,众多学者就其机理进行了研究,但仍无确定性方法预测一个边坡是会持续缓慢变形还是会转化为大规模的崩塌破坏。

本文以反倾层状岩质边坡为研究对象,归纳了倾倒变形的主要影响因素,介绍了采用物理模型试验方法、极限平衡方法、数值模拟方法对倾倒变形机理的研究进展,指出了这3种方法的适用性和优缺点,说明了研究中需要进一步改进和深化的内容。

1 倾倒变形分类

倾倒多发生在由塑性的薄层岩层或软硬相间组成的反坡向结构的边坡中。岩层的倾倒以弯曲、张裂、滑动和转动等形式出现,倾倒体与下伏完整岩体间可产生折断或错动[1]。通常,倾倒变形模式按倾倒方式的不同主要可分为以下3类[3](见图1)。

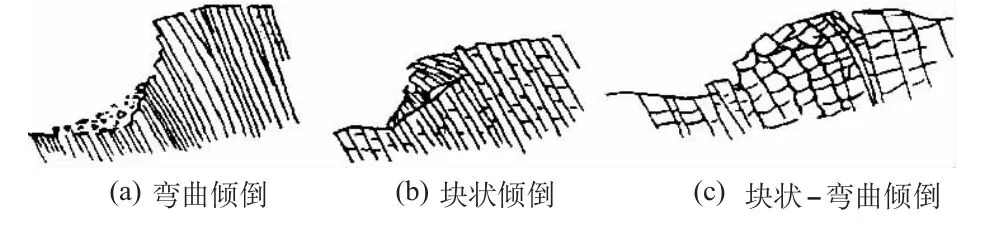
图1 岩层倾倒变形模式Fig.1 Rock-stratification Toppling modes

(1)弯曲倾倒(flexural toppling):弯曲倾倒为柔性破坏,较软岩层中较为普遍,如板岩、千枚岩、片岩、泥岩[3]。通常单一岩层厚度较小,只有层面这一组平行结构面。弯曲倾倒变形边坡属于自稳型,边坡变形发展较慢,一旦破坏,规模通常很大。

(2)块状倾倒(block toppling):块状倾倒为脆性破坏,硬质岩层中较为普遍,多发生在石灰岩、砂岩、含柱状节理的岩浆岩中[3]。通常单一岩层厚度较大,发育与岩层面接近垂直的节理,破坏前变形较快。

(3)块状-弯曲倾倒(block-flexure toppling):软硬相间的层状岩体中比较普遍,多发生在砂岩泥板岩互层、燧石岩页岩互层、薄层状石灰岩中[3]。软硬相间的层状岩体在构造作用下存在层间错动[13]。可在弯曲倾倒变形稳定性分析的基础上,考虑垂直层面方向的节理或裂隙对边坡稳定的影响,从而实现此类倾倒模式的稳定性分析。

目前国内外对倾倒变形的研究主要集中于块状倾倒和弯曲倾倒。

2 倾倒变形影响因素

边坡产生倾倒变形的影响因素有很多。韩贝传、王思敬(1999)[14]把倾倒变形的影响因素归纳为:初始应力场、边坡初始坡型、边坡开挖深度与角度、岩体与层面力学参数、层面几何特性即层面间距与倾角、开挖后地下水位变化等。齐典涛(2001)[8]关于昌马水库倾倒变形影响因素有:层理、裂隙、断层走向,地形地貌、地质构造影响,卸荷作用,冰川活动时对岩层顶端的拖曳作用,冰劈作用。徐佩华等(2004)[6]认为解放沟反倾高边坡深层变形是由河谷快速下切产生深部卸荷松弛和倾内层状体斜坡的深部岩层弯曲倾倒共同作用所引起的。

在边坡倾倒变形的影响因素中,岩层强度、岩层长细比、岩层倾角、层面力学参数、与层面正交或斜交的节理组力学参数和连通率、开挖作用对边坡变形影响的研究较多,考虑水、岩体属性随深度变化(考虑风化和卸荷)的研究较少。其中地下水的研究仅限极限平衡法及少量模型试验研究,未见数值模拟方面的文献。伍法权(1997)[15]以库仑强度理论为依据,对薄片状云母石英片岩斜坡弯曲倾倒变形进行分析,讨论了地下水压力的作用。常祖峰等(1999)[11]考虑了开挖和地下水作用对小浪底工程库区岸坡倾倒变形的影响。李天扶(2006)[16]认为倾倒破坏稳定分析中,应计入上层滞水产生的倾倒力矩,这样才能解释倾倒体的许多不规则现象。文[9,17～19]对岩层倾角、层面间距和层面力学参数进行了研究,得出了一些定性或定量的结论。

综上所述,反倾岩质边坡倾倒变形的主要影响因素可归纳为如下几个方面:

(1)边坡几何形状(坡高,坡角),其中坡高对倾倒变形的影响研究较少。

(2)岩层强度、厚度(岩层长细比)、倾角,层面力学参数:较硬岩层易产生块状倾倒,较软岩层易产生弯曲倾倒,软硬相间岩层易产生块状-弯曲倾倒,岩层倾角对边坡变形影响不大。许多学者认为,对边坡倾倒变形影响最大的因素有2个,即层面的间距(等效于层面之间板状岩体的长细比)及力学参数[14]。卢增木等(2006)[18]、左保成等(2005)[17]通过模型试验得出层面剪切强度对倾倒变形影响较大,而JoséMuralha(2003)[20]通过参数研究认为层面和折断面的剪切强度不像预计的那样起重大作用。作者认为,对于这一点,需要进一步深入研究。

(3)与层面正交或斜交的节理组的产状、连通性和间距。

(4)初始构造应力场[9,14]。

(5)外力作用:如河谷下切,开挖作用,风化卸荷作用,冰劈作用,冰川运动,上覆岩体的压力作用,地震作用等。

(6)地下水:层面遇水后抗剪强度降低,层间错动能力加强,层间裂隙水压力或冻融作用亦可增大岩层的倾倒弯矩,加剧岩层的倾倒变形发展[16]。

3 倾倒变形机理研究

倾倒变形机理的研究方法通常有物理模型试验法、极限平衡法及数值模拟法。这3种方法的具体研究进展如下。

3.1 物理模型试验方法

物理模拟试验方法虽然周期长、费用高,但可直观地模拟边坡岩体中的应力大小及其分布,能直接观测和记录岩体的变形、破坏机制及其发展过程。

黄润秋等(1994)[21]通过模型试验得出了变形深度与岩层倾角、坡角的关系。该研究较有意义,若能根据岩层倾角和坡角定性获悉变形深度情况及其变化趋势,则有助于边坡稳定性的判别和预测。罗华阳等(2000)[10]对五强溪水电站左岸船闸边坡某断面进行了模型试验,发现开挖卸荷后变形明显,裂隙渗透水引起的变形比开挖引起的变形大,有较大参考价值。左保成等(2005)[17]发现反倾边坡主要的破坏形式为倾倒变形折断破坏,破坏首先发生在坡顶;层面强度和厚度是影响边坡稳定性的重要因素,而岩层倾角对变形影响不大;此类边坡的变形破坏过程具有明显的“叠合悬臂梁”特征。这些模型试验对工程实际皆具有指导意义。

D.P.Adhikary(2007)[22]通过离心试验发现,弯曲倾倒模式下,假定层间作用力为集中力时,作用点在0.55～0.60层高处。层面摩擦角较大时弯曲倾倒破坏为瞬时性,摩擦角较小时弯曲倾倒破坏为渐进性,决定破坏模式的关键摩擦角度值为20°～25°。凝聚力对破坏机理的影响和摩擦角不一样。Cavers (1981)用Euler buckling load原理分析了沉积岩层的弯曲破坏,在底摩擦试验的基础上,发现产生弯曲的岩层长度与岩层总长度的比率(buckling ratio)为0.36～0.46。这个固定buckling ratio的假定并不适用所有不同几何性质的边坡。实际上,buckling ratio必须是关于边坡几何参数的函数[23]。

综上所述,模型试验有助于得出一些规律,但是其结果有局限性,不一定具普遍意义,如buckling ratio必须是关于边坡几何参数的函数[23];模型试验结果用于极限平衡计算时也要谨慎。此外,模型试验方面应加强考虑与层面相交的节理、地下水作用和边坡几何形状对倾倒变形影响的研究,这也对模型设计提出了更高的要求。

3.2 极限平衡方法

极限平衡方法避开了广泛的应力计算,关注瞬时破坏前的状态,模型简单,计算快捷,对边坡稳定性的初步估计是合适的。

Goodman和Bray(1976)[3]首先采用极限平衡方法(简称G-B法)进行了分析,模型示意图见图2。该方法假定台阶状的破坏面和均一的岩柱宽度和台阶高度,未反映出岩体结构面的分布情况;结构面完全连通,未考虑岩桥作用[24],假定岩层间传递的推力作用点位于岩层面接触处顶部[25]。Duncan (1992)[26]在G-B模型的基础上,增加了作用于板状岩体层间和倾倒岩体底面上的水压力及在倾倒体上部外荷载的作用,并给出了基本解析式。李天扶(2006)[16]认为Duncan把水压力按岩石块体的斜高计算是错误的,应按水柱的垂直高度计算。陈祖煜(1996)[27]进行了G-B法的改进,考虑了岩柱底滑面的连通率,定义了安全系数,改进了破坏模式的判定方法,考虑了底面和侧面不正交的一般情况。汪小刚等(1996)[25]也对G-B法进行了改进,考虑了岩体结构面的具体分布特征和底滑面上岩桥的作用。

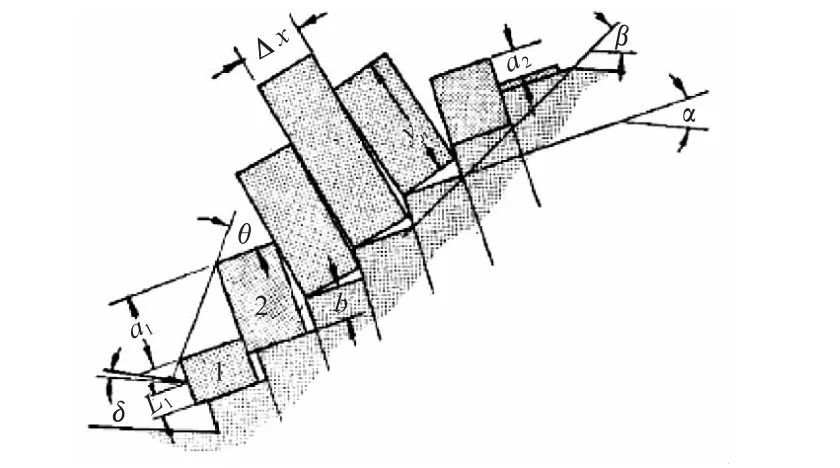
图2 倾倒极限平衡分析模型(据Goodman和Bray,1976)Fig.2 Model for limiting equilibrium analysis of toppling (from Goodman and Bray,1976)

关于其它极限平衡方法的研究,朱继良等(2004)[12]通过用简化毕肖普法对该滑坡进行了稳定性计算,分析了随着水位升降以及地震下边坡稳定性的变化情况。Aydan(1992)假定层间作用力为集中力,作用点根据试验结果估计确定。破坏面是单一直线状,从最上部的岩层算起,推到最下面的岩层,各自建立力矩平衡方程,推断边坡的稳定性。A.Bobet (1999)[28]在Hoek和Bray,Aydan等人研究基础上,假定块体厚度很小,对块状倾倒模式进行了无渗流和有渗流两种情况下极限平衡方法的探讨。

基于极限平衡原理的分析方法有很大局限性,适用于岩层厚度较大、边坡形状较简单和受简单荷载作用的情况,考虑的是均匀介质的简单破坏模式,这与边坡倾倒变形受反倾结构面决定性控制的实际情况相差甚远。这些限制制约了块体倾倒破坏分析方法的推广应用[5]。还有学者认为,倾倒变形破坏首先在坡顶产生,极限平衡假设滑动面的方法不适用于倾倒变形的研究[14]。孙广忠(1985)[13]提出板裂结构岩体的力学作用遵守板梁结构变形和破坏法则,板梁弯曲和结构失稳的力学模型是它的基本力学模型。Adhikary(2007)[22]认为极限平衡模型可以预测高节理(即层面)摩擦角值条件下的破坏荷载,但在节理摩擦角值较小的情况下会高估破坏荷载,因此,建议节理摩擦角较小时谨慎使用极限平衡方法。

综上,边坡的稳定性计算中,若仅关注边坡的最终破坏,且满足极限平衡假定,则极限平衡方法可用作边坡稳定性分析的初步估计。若预先假定破坏面位置则会限制极限平衡模型的应用。关于破坏面形状,目前所见的国内外文献中,多假定块状倾倒型边坡的破坏面为阶梯形,弯曲倾倒型边坡的破坏面为直线形,未见块状-弯曲倾倒型边坡的极限平衡计算。此外,岩层间的相互作用力通常被假设为集中荷载或均布力形式,还可进行力的其它分布形式的研究。考虑岩体在外荷载作用下(如上覆岩体的压力作用、地下水作用等)的极限平衡分析更具普遍意义。鉴于不同学者对极限平衡方法适用性持有的不同看法,尚须对此进一步深入研究。

3.3 数值模拟方法

基于连续介质力学和非连续介质力学的数值模拟方法在边坡稳定性分析中得到了广泛运用,它对原型的反映不仅仅是单变量的趋势相似,而且模型本身能反映滑坡体的形成机制[6]。目前主要研究方法的进展如下。

3.3.1 连续介质力学方法

常见的是采用接触单元模拟层面的有限元法和有限差分法。韩贝传、王思敬(1999)[14]应用弹-粘塑性模型,研究了层面间距及力学参数对变形的影响,发现切向变形刚度值和层面间距对坡顶位移影响很大。常祖峰(1999)[11]应用非线性理论对单层倾倒变形破坏进行了有限元模拟,结果与野外实测剖面非常吻合。徐佩华等(2004)[5]采用FLAC3D进行倾倒变形机制的三维数值模拟,认为坡体卸荷和卸荷回弹促进弯曲倾倒变形的进行,并为变形划定界限,发现破坏面为双折线型。J.SJ¨OBERG (1999)[29]采用FLAC中的遍布节理模型进行了大规模弯曲倾倒变形破坏机理的研究。

当层面刚度很大,等效连续介质和单个岩层的有效剪切模量差别不大时,层面滑动很小,岩层弯曲可以忽略。当节理剪切刚度很小时,岩层滑动时可能会产生弯曲。若不计材料抵抗弯曲的作用,等效连续介质模型可能会高估变形量。此外,岩层数目较多或岩层相对较薄时,模拟过程麻烦且需要较高的计算机处理能力。若等效成连续介质模型,同时采用能考虑岩层抵抗弯曲作用的理论[30],提供一个广义上的对此类介质的平均描述会更有意义。

建立在Cosserat理论上的有限元法是研究弯曲倾倒破坏机理[22]的一个较好手段。国内佘成学[31]、陈胜宏、葛修润等较早进行了这方面的研究。国外学者D.P.Adhikary在这方面也有很多研究成果:1996年他利用Cosserat理论实现了层状边坡弯曲倾倒变形过程的有限元分析,但由于小变形的假设,应用受到限制[32]。1998年他在带弹塑性节理的Cosserat模型中整合入大变形公式,模型得到进一步完善[33]。

作者认为,建立在Cosserat理论上的能考虑岩层转动效应和大变形的连续介质力学模型是研究边坡倾倒变形机理的一个较好方法,但是经典连续介质的屈服准则无法直接用于Cosserat连续介质,所以需要发展相应的合适的屈服准则。李银平、刘俊、李育超等已经展开了相关研究,但多为简单荷载情况,尚未见到考虑地下水作用的相关文献,否则可以更广泛地解决边坡倾倒变形问题。

3.3.2 非连续介质力学方法

当岩体被节理切割成离散又相互作用的块体时,应用非连续介质力学方法,能直接反映结构面对边坡变形的影响。

J.SJ¨OBERG(1999)[29]采用UDEC进行了大规模弯曲倾倒变形破坏机理的研究,倾倒破坏整个过程见图3。岩层产生弹性反弹后,岩体破坏始于坡脚陡倾角节理面上的剪切滑动,然后逐渐向坡顶发展,其间应力重分布;岩层被压缩,为转动提供空间,转动岩层基部开始出现张拉弯曲破坏并逐渐向边坡顶部发展,最后岩层基部破坏面贯穿,产生滑坡。

F.Lannro等(1997)[34]用离散元法模拟模型试验的块体倾倒,考虑了模型试验倾斜台的转动速率、块体间接触面的摩擦角、块体边角的的圆弧长度、模型内部和接触面上的速度分布等因素的影响。Susan L.Nichol等(2002)[35]利用UDEC进行了参数(岩体强度、结构面方位和连通率)和机理研究。程东幸等(2005)[9]借助3DEC对龙滩水电站左岸边坡进行了影响因素及反倾条件分析。DDA及数值流形方法在倾倒变形研究中亦有应用。

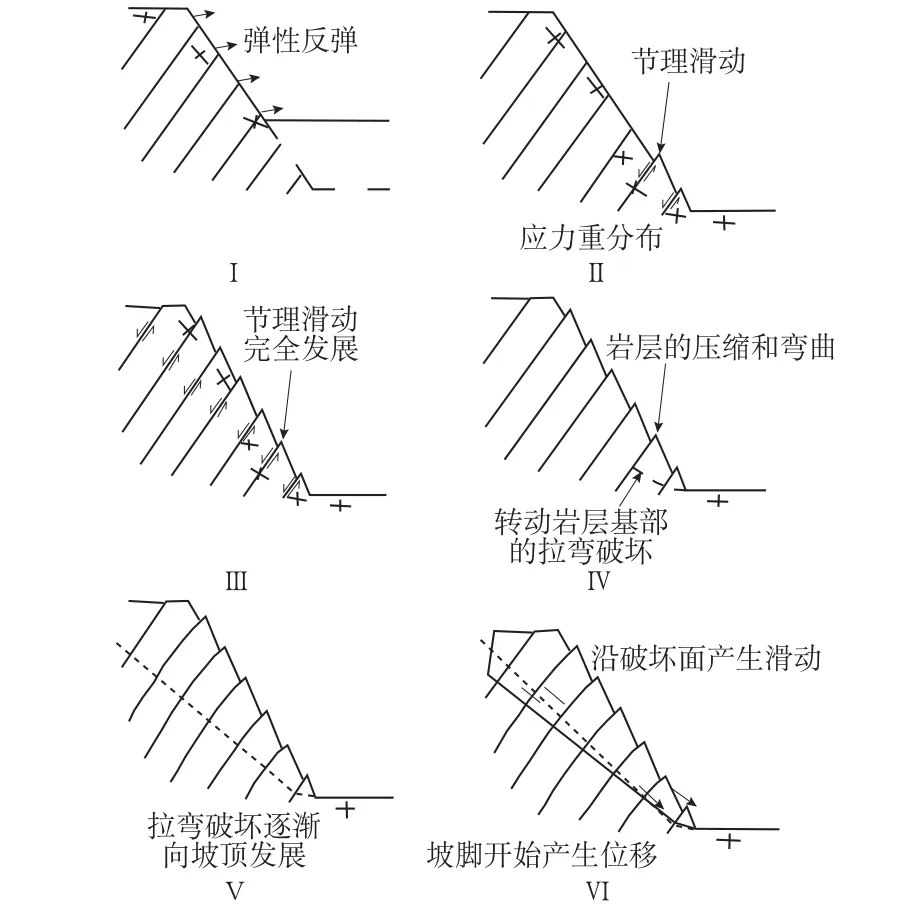
图3 边坡大规模弯曲倾倒破坏的演化过程Fig.3 Failure stages for large scale(flexural) toppling failure in a slope

尽管有的非连续介质力学分析方法还存在一定问题,如计算量大、收敛性差等,特别当岩层数目过多时模型处理会比较麻烦,但能直观反映倾倒变形边坡破坏的过程。若能把握好岩体介质模型并选择合理的参数,可以得到理想的计算结果。

3.4 研究方法小结

关于倾倒变形机理的研究方法,模型试验应加强其它影响因素(地下水、与层面相交的节理分布、边坡几何形状等)的研究。极限平衡法能满足边坡稳定性初步估计的要求,但在倾倒变形边坡稳定性分析中的适用性有待于进一步深入讨论;数值模拟方面,模拟过程应能考虑层面和与其正交或斜交的节理裂隙影响、岩层的转动变形和层间错动、渗流作用等,并建立有效的屈服准则,确定合理的参数,来尽量准确地研究其变形机制。

4 结论

通过对倾倒变形影响因素的分析以及3种不同研究方法下倾倒变形机理研究的论述,得出以下结论:

(1)反倾岩质边坡倾倒变形的影响因素很多,其中边坡几何形状、层面间距和力学参数、与层面正交或斜交的结构面产状和连通率、岩层强度、地下水和开挖作用等影响较大。

(2)数值模拟是较有发展前景的方法,其中,建立在Cosserat理论上的连续介质方法有一定优势,模型建立简单且能考虑岩层的弯曲效应,关键是层状岩体力学参数的确定以及合适的屈服准则的建立,并应用于实际边坡工程,进而对倾倒变形边坡的稳定性进行分析预测。

(3)倾倒变形机理研究还有许多工作须要加强。如对软硬互层岩体边坡的研究、水对倾倒变形影响的研究等。与层面正交或斜交的节理面的连通率是倾倒变形的重要影响因素,野外踏勘时应注意折断错动面的贯通情况,勘查边坡是否有后缘张裂、坡脚剪切破坏的现象。此外,考虑开挖、降雨、地震等的影响也是一个重要方面。

倾倒变形机理比较复杂,它与滑动破坏机理完全不同,没有单一的滑动基面。目前仍无确定性方法预测一个边坡是会持续缓慢变形还是会转化为大规模的崩塌破坏。因此,倾倒变形机理研究对于防止边坡产生更大变形甚至失稳及灾害评估有重大意义。条件允许情况下可进行边坡动态监测,反演岩体力学参数,对其变形和破坏发展作出评估。进一步研究反倾层状岩质边坡破坏的发生机理和运动机制仍然是当前边坡工程研究的重点课题。

[1]陆兆臻.工程地质原理[M].北京:中国水利水电出版社,2001.

[2]黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(32):433-454.

[3]GOODMAN R E,BRAY J W.Toppling of Rock Slopes [C]∥.ASCE/Bouider.Proceeding of the Specialty Conference on Rock Engineering for Foundations and Slopes. Colorado,1976,201-234.

[4]王思敬.金川露天矿边坡变形机制及过程[J].岩土工程学报,1982,4(1):76-83.

[5]徐佩华,陈剑平,黄润秋,等.锦屏Ⅰ级水电站解放沟左岸边坡倾倒变形机制的3D数值模拟[J].煤田地质与勘探,2004,32(4):40-43.

[6]徐佩华,陈剑平,黄润秋,等.锦屏水电站解放沟反倾高边坡变形机制的探讨[J].工程地质学报,2004,12 (3):247-252.

[7]杨根兰,黄润秋,严明,等.小湾水电站饮水沟大规模倾倒破坏现象的工程地质研究[J].工程地质学报, 2006,14(2):165-171.

[8]齐典涛.昌马水库倾倒变形边坡特征形成机制及发育深度[J].西部探矿工程,2001,(6):47-49.

[9]程东幸,刘大安,丁恩保,等.层状反倾岩质边坡影响因素及反倾条件分析[J].岩土工程学报,2005,27 (11):1362-1366.

[10]罗华阳,王敬,谢新宇,等.五强溪水电站左岸边坡位移监测与变形特征[J].大坝观测与土工测试, 2000,24(3):22-24.

[11]常祖峰,谢阳,梁海华.小浪底工程库区岸坡倾倒变形研究[J].中国地质灾害与防治学报,1999,10(11): 28-31,27.

[12]朱继良,黄润秋,王运生,等.某水电站洼里滑坡的成因机制及其稳定性研究[J].中国地质灾害与防治学报,2004,15(1):57-60.

[13]孙广忠,张文彬.一种常见的岩体结构-板裂结构及其力学模型[J].地质科学,1985,(3):275-282.

[14]韩贝传,王思敬.边坡倾倒变形的形成机制与影响因素分析[J].工程地质学报,1999,7(3):213-217.

[15]伍法权.云母石英片岩斜坡弯曲倾倒变形的理论分析[J].工程地质学报,1997,5(4):306-311.

[16]李天扶.论层状岩石边坡的倾倒破坏[J].西北水电, 2006,(4):4-6.

[17]左保成,陈从新,刘小巍,等.反倾岩质边坡破坏机理模型试验研究[J].岩石力学与工程学报,2005,24 (19):3505-3511.

[18]卢增木,陈从新,左保成,等.对影响逆倾层状边坡稳定性因素的模型试验研究[J].岩土力学,2006,27(4): 629-632,647.

[19]ADHIKARY DP,DYSKIN A V,JEWELL RJ,et al.A Study of the Mechanism of Flexural Toppling Failure of Rock Slopes[J].Rock Mechanics and Rock Engineering, 1997,30(2):75-93.

[20]JOSéM.Parameter Variability in the Toppling Stability of Rock Blocks[C]∥Matthew Huandley,Dick Stacey. 10th Congress of the ISRM:Technology Roadmap for Rock Mechanics,Johannesburg,South Africa:South African Institute of Mining and Metallurgy.2003:849-854.

[21]黄润秋,王峥嵘,许强.反倾向层状结构岩体边坡失稳破坏规律研究[C]∥成都理工学院工程地质研究所工程地质研究进展(二).成都:西南交通大学出版社, 1994:47-51.

[22]ADHIKARY D P,DYSKIN A V.Modelling of Progressive and Instantaneous Failures of Foliated Rock Slopes [J].Rock Mechanics and Rock Engineering,2007,40 (4):349-362.

[23]PANT S R,ADHIKARY D P.Implicit and Explicit Modelling of Flexural Buckling of Foliated Rock Slopes [J].Rock mechanics and rock engineering.1999,32 (2):157-164.

[24]张国新,赵妍,石根华,等.模拟岩石边坡倾倒破坏的数值流形法[J].岩土工程学报,2007,29(6):800-805.

[25]汪小刚,贾志欣,陈祖煜,等.岩质边坡倾倒破坏的稳定分析方法[J].水利学报,1996,(3):7-12,21.

[26]DUNCAN C W.Foundations on Rock(Second Edition) [M]∥London:SPON E F N,1999.

[27]陈祖煜,张建红,汪小刚.岩石边坡倾倒稳定分析的简化方法[J].岩土工程学报,1996,18(6):92-95.

[28]BOBET A.Analytical Solutions for Toppling Failure[J]. Mechanics and Mining Science,1999,36:971-980.

[29]SJ¨OBERG J.Analysis of Failure Mechanisms in High Rock Slopes[C]∥Gerard Vouille,Pierre Berest Proceeding of the Ninth International Congress on Rock Mechanics.Paris,Taylor and Francis Group,1999:127-130.

[30]ADHIKARY D P,DYSKIN A V.A Cosserat Continuum Model for Layered Materials[J].Computers and Geotechnics,1997,20(1):15-45.

[31]李桂荣,佘成学,陈胜宏.层状岩体边坡的弯曲变形破坏试验及有限元分析[J].岩石力学与工程学报, 1997,16(4):305-311.

[32]ADHIKARY DP,DYSKIN A V,JEWELL RJ.Numerical Modeling of the Flexural Deformation of Foliated Rock Slopes[J].Rock Mechanics and Mining Science, 1996,33(6):595-606.

[33]ADHIKARY D P,MüHLHAUS H B,DYSKIN A V. Modelling the Large Deformations in Stratified Media—the Cosserat Continuum Approach[J].Mech.Cohes.-Frict.Mater,1999,(4):195-213.

[34]LANAR F,JING L,STEPHANSSON O,et al.D.E. M.Modeling of Laboratory Tests of Block Toppling[J]. Rock Mechanics and Mining Sciences,1997,34(3-4): 173.el-173.e15.

[35]NICHOL S L,HUNGR O,EVANS S G.Large-scale Brittle and Ductile Toppling of Rock Slopes[J].Canadian Geotechnical Journal,2002,39(4):773-787.

(编辑:赵卫兵)

Overview of Toppling Failure Mechanism of Countertendency Layered Rock Slopes

ZOU Li-fanga,b,XU Wei-yaa,b,NING Yua,b,ZHENG Wen-tanga,b
(a.Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University,Nanjing 210098,China; b.Research Institute of Geotechnical Engineering,Hohai University,Nanjing 210098,China)

Toppling deformation failure is common in layered rock slope projects.It makes sense to research on toppling failure mechanism in slope stability analysis.On the basis of the relevant research both at home and abroad,three main different failure modes of toppling deformation are analyzed.They are flexural toppling, block toppling and block-flexure toppling.Influential factors of toppling deformation like the geometrical shape of slopes,rock strength and the ratio of length to thickness for layers,mechanical parameters of interface, groundwater,excavation effect and so on,are illustrated.Corresponding research methods mainly include physical model tests,limiting equilibrium methods and numerical simulation,with which research headway is presented.Applicability,advantages and disadvantages of those methods when studying toppling failure are pointed out at the same time.Then specific issue to be improved and further studied is proposed.

toppling deformation;failure mechanism;layered slope;numerical simulation

TU457

A

1001-5485(2009)05-0025-06

2008-07-30;

2008-11-10

国家自然科学基金重点项目(50539110);国家重点基础研究发展规划973项目(2002CB412707)

邹丽芳(1982-),女,江苏无锡人,博士研究生,主要从事岩石力学与工程方面的研究工作,(电话)025-83787037(电子信箱)zoulifang@hhu.edu.cn。