一个包含Z(n)和D(n)函数的方程及其它的正整数解

葛键

(西安财经学院统计学院,陕西西安 710061)

一个包含Z(n)和D(n)函数的方程及其它的正整数解

葛键

(西安财经学院统计学院,陕西西安 710061)

对于任意正整数n,著名的伪Smarandache函数Z(n)定义为最小的正整数m使得n|m(m+1)/2.而数论函数D(n)定义为最小的正整数m使得n|d(1)d(2)d(3)…d(m),其中d(n)为Dirichlet除数函数.本文的主要目的是利用初等方法研究一类包含伪Smarandache函数Z(n)和数论函数D(n)的方程2Z(n)=D(n)的可解性,并获得了该方程的所有正整数解.

伪Smarandache函数Z(n);函数D(n);初等方法;方程;正整数解

1 引言及结论

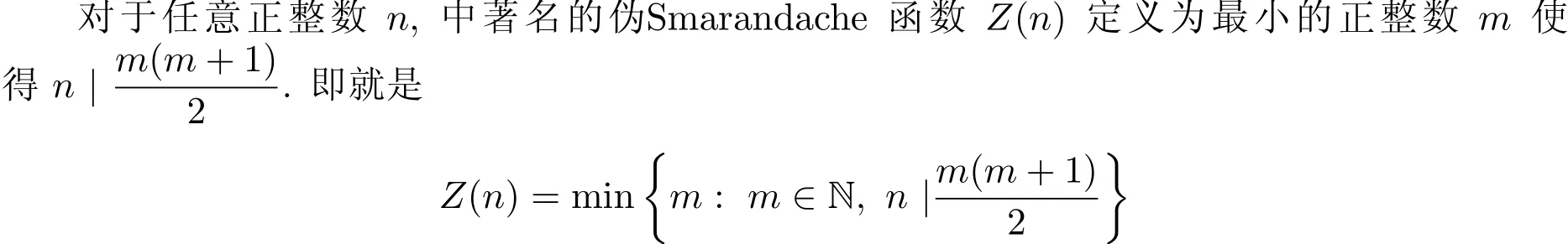
例如：Z(1)=1,Z(2)=3,Z(3)=2,Z(4)=7,Z(5)=4,Z(6)=3,Z(7)=6,Z(8)= 15,Z(9)=8,Z(10)=4,Z(11)=10,Z(12)=8,Z(13)=12,Z(14)=7,Z(15)=5, Z(16)=31,Z(17)=16,Z(18)=8,Z(19)=18,….这一函数是美籍罗马尼亚著名数论专家Smarandache教授中提出的[1],并建议人们研究它的性质.关于这一问题,许多学者进行了研究,获得了不少有价值的研究结果[25].例如文[2]的作者中利用初等方法及其素数分布定理给出了渐近公式X

其中c1和c2为常数.这是两个没有解决的问题.

另一方面,在文[8]中,作者引入了一个新的数论函数D(n),它定义为最小的正整数m使得n|d(1)d(2)d(3)…d(m),其中d(n)为Dirichlet除数函数.即就是

例如：D(1)=1,D(2)=2,D(3)=4,D(4)=3,D(5)=24,D(6)=4,D(7)=26,D(8)=4, D(9)=9,D(10)=16,D(11)=210,D(12)=4,D(13)=212,D(14)=64,D(15)=16, D(16)=6,…,D(p)=2p−1,其中p为素数.关于D(n)的一些初等性质,文[7]以及文[8]都进行了研究,文[7]还利用解析方法给出了渐近公式

这里k为任意给定的正整数,ci(i=2,3,…,k)是可计算的常数.

最近,张文鹏教授建议我们研究一个包含数论函数D(n)及伪Smarandache函数Z(n)的方程2Z(n)=D(n)的可解性,并求出它的所有正整数解.关于这一问题,目前似乎没有人进行研究,至少我们没有看到过这方面的文章.本文利用初等方法研究了这一问题,并得到完全解决.具体地说也就是证明了下面的:

2 定理的证明

这节我们利用初等方法以及Z(n)和D(n)的性质直接给出定理的证明.关于Z(n)的性质,参阅文[34].关于D(n)的性质,只有文[8]中讨论的比较仔细,可以参考.现在我们分以下几种情况进行讨论:

[1]Smarandache F.Only Problems,Not Solutions[M].Chicago:Xiquan Publishing House,1993.

[2]Lou Yuanbing.On the pseudo the Smarandache function[J].Scientia Magna,2007,3(4):48-50.

[3]Le Maohua.Two functional equations[J].Smarandache notions journal,2004,14:180-182.

[4]张文鹏.关于Smarandache函数的两个问题[J].西北大学学报,2008,173(2):173-176.

[5]Daivd Gorski.The Pseudo-Smarandache function[J].Smarandche Notions,2002,13:140-149.

[6]Hardy G H,Wright E M.An Introduction to the Theory of Numbers[M].Oxford:Oxford Univ.Press,1937.

[7]Shang Songye,Chen Guohui.An New Smarandache Multiplicative Function and Its Mean Value Formula, Research on Number Theory and Smarandache Notions(Collected Papers)[M].USA:Hexis,2009.

[8]Li Ling.An new Smarandache Multiplicative Function and Its Arithmetical Properties,Research on Number Theory and Smarandache Notions(Collected Papers)[M].USA:Hexis,2009.

[9]Apostol T M.Introduction to Analytic Number Theory[M].New York:Springer-Verlag,1976.

An equation involving the functions Z(n)and D(n) and its all positive integer solutions

GE Jian
(School of Statistics,Xi’an University of Finance and Economics,Xi’an710061,China)

For any positive integer n,the famous pseudo Smarandache function Z(n)is defined as the smallest positive integer m such that n|m(m+1)/2.The number theory function D(n)is defined as the smallest positive integer m such that n divides d(1)d(2)…d(m),where d(n)is the Dirichlet divisor function.The main purpose of this paper is using the elementary method and the properties of the pseudo Smarandache function Z(n)and number theory function D(n)to study the solvability of the equation 2Z(n)=D(n),and obtain its all positive integer solutions.

the pseudo Smarandache function Z(n),function D(n),elementary method,equation,positive integer solutions

O156.4

A

1008-5513(2009)03-0622-03

2008-06-05.

国家自然科学基金(10671155),陕西省教育厅自然科学基金(08JK291).

葛键(1961-),副教授,研究方向：基础数学.

2000MSC:11B83,58F08