非齐型齐次Morrey-Herz空间中某些次线性算子和交换子的有界性

武江龙

(牡丹江师范学院数学系,黑龙江牡丹江 157012)

非齐型齐次Morrey-Herz空间中某些次线性算子和交换子的有界性

武江龙

(牡丹江师范学院数学系,黑龙江牡丹江 157012)

在非齐型齐次Morrey-Herz空间(µ)中建立了某些次线性算子的有界性,同时利用Calder´on-Zygmund算子的L2(µ)有界性,在(µ)上证明了由Calder´on-Zygmund算子和RBMO(µ)函数生成的交换子的有界性.

交换子;齐次Morrey-Herz空间;非二倍测度;RBMO(µ);次线性算子

1 引言

在经典调和分析中,一个关键的假设是测度满足二倍条件.我们称测度µ满足二倍条件,是指如果存在常数C,使得对x∈suppµ,r＞0,有µ(B(x,2r))≤Cµ(B(x,r)),其中B(x,r)={y∈Rd:|y−x|＜r}.然而,最近几年的研究表明,定义在欧氏空间Rd上的非负Radon测度µ不满足二倍条件时,许多经典的结果仍然成立[15].对µ仅有的假设条件是增长性条件,即存在常数C0＞0,使得对任意的x∈Rd,r＞0,有

其中n为固定的数且0＜n≤d.如果欧氏空间Rd上赋予的Radon测度仅满足增长性条件(1),则称它为非齐型空间.众所周知,二倍条件在齐型空间的分析中起着关键作用,这表明齐型空间上调和分析理论和非二倍测度下的结果是截然不同的[14].

2 次线性算子在非齐型齐次Morrey-Herz空间中的有界性

在叙述主要结果之前,首先回顾一些基本概念.

对于k∈Z,令Bk={x∈Rd:|x|≤2k},Ak=BkBk−1和χk=χAk,其中χAk表示集合Ak的特征函数.

其中Q⊂Rd为各边平行于坐标轴的闭方体,l(Q)表示其边长.文[11]证明了极大函数M在Lq(µ)(1＜q＜∞)中有界.并且容易验证M满足定理2.1中的尺寸条件(i)和(ii).从而有

推论2.2设α,λ,p和q如定理2.1中所述,则由(4)式定义的极大函数M在中有界.

注当λ=0时,上面的结果和文[8]中得到的结果是一致的.

3 交换子在非齐型齐次Morrey-Herz空间中的有界性

本节主要讨论Calder´on-Zygmund算子和RBMO(µ)函数生成的交换子在齐次Morrey-Herz空间中的有界性.

对于给定的常数γ＞1,β＞γn及βd=2inf β,称某个方体Q⊂Rd是一个(γ,β)倍方体是指Q满足µ(γQ)≤βµ(Q),其中γQ表示与Q同心,边长为γl(Q)的方体.对于Rd中给定的两个方体Q1⊂Q2,定义

从而由引理3.1得

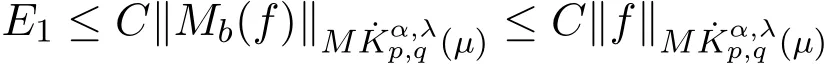
对E3,注意到,当x∈Ak,j≥k+2以及y∈Aj时,有|x−y|～|y|,因此,对j≥k+2,运用RBMO(µ)函数的性质,H¨older不等式,K˜Qk,˜Qj≤C(j−k−1),(a),增长性条件(1)及文[4]中的推论3.5,有

注当λ=0时,上面的结果和文[8]中得到的结果是一致的.

[1]Orobitg J,P´erez C.Apweights for non doubling measures in Rnand applications[J].Trans.Amer.Math. Soc.,2002,354:2013-2033.

[2]Hu Guoen,Meng Yan,Yang Dachun.New atomic characterization of H1space with non-doubling measures and its applications[J].Math.Proc.Cambridge Philos.Soc.,2005,138(1):151-171.

[3]Hu Guoen,Meng Yan,Yang Dachun.Multilinear commutators of singular integrals with non doubling measures[J].Integral Equations Operator Theory,2005,51(2):235-255.

[4]Tolsa X.BMO,H1and Calder´on-Zygmund operators for non doubling measures[J].Math.Ann.,2001, 319:89-149.

[5]Tolsa X.Littlewood-Paley theory and the T(1)theorem with non-doubling measures[J].Adv.Math.,2001, 164:57-116.

[6]Li Xinwei,Yang Dachun.Boundedness of some subinear operators on Herz spaces[J].Illinois J.of Math., 1996,40:485-501.

[7]Lu Shanzhen,Yang Dachun.The continucity of commutators on Herz-type spaces[J].Michigan Math.J., 1997,44:255-281.

[8]郭燕,孟岩.某些次线性算子和交换子在非齐型空间上的Herz空间中的有界性[J].北京师范大学学报:自然科学版,2004,40(6):725-731.

[9]赵向青,高文华.线性算子在Herz-Morrey空间上的有界性[J].高校应用数学学报:A辑,2005,20(1):55-62.

[10]孟岩.非倍测度空间上极大交换子有界性的新证明[J].北京师范大学学报:自然科学版,2004,40(3):309-314.

[11]Garc´ıa-Cuerva J,Martell J M.Two-weight norm inequalities for maximal operators and fractionals on non-homogeneous spaces[J].Indiana Univ.Math.J.,2001,50:1241-1280.

Boundedness of some sublinear operators and commutators on homogeneous Morrey-Herz spaces with non doubling measures

WU Jiang-long
(Department of Mathematics,Mudanjiang Normal College,Mudanjiang157012,China)

The boundedness of some sublinear operators is established on homogeneous Morrey-Herz spaces with non-doubling measures.At the same time,this paper using the L2(µ)boundedness of Calder´on-Zygmund operators to prove the boundedness of commutators generated by Calder´on-Zygmund operators with RBMO(µ) functions on

commutator,homogeneous Morrey-Herz space,non-doubling measure,RBMO(µ),sublinear operator

O174

A

1008-5513(2009)03-0586-09

2007-06-21.

牡丹江师范学院科研项目(KZ2008001).

武江龙(1980-),硕士,研究方向：调和分析.

2000MSC:42B25