ρ混合序列的完全收敛性和部分和的几乎处处收敛性

冯凤香

(桂林理工大学理学院,广西桂林 541004)

ρ混合序列的完全收敛性和部分和的几乎处处收敛性

冯凤香

(桂林理工大学理学院,广西桂林 541004)

讨论了不同分布ρ混合序列的完全收敛性和部分和的几乎处处收敛性,利用矩不等式和截尾方法，得到了和独立情形完全一样的结果.

ρ混合序列;完全收敛;强收敛;矩条件

1 引言及引理

设{Xi,i∈N}是概率空间(Ω,β,P)上的随机变量序列,Fs=σ(Xi,i∈S⊂N)为σ−域, 在β中给定σ-域F,R,令

2 主要结果

3 定理的证明

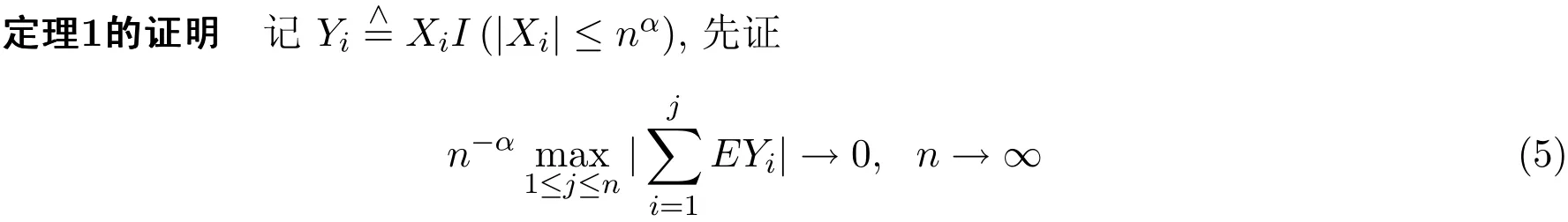
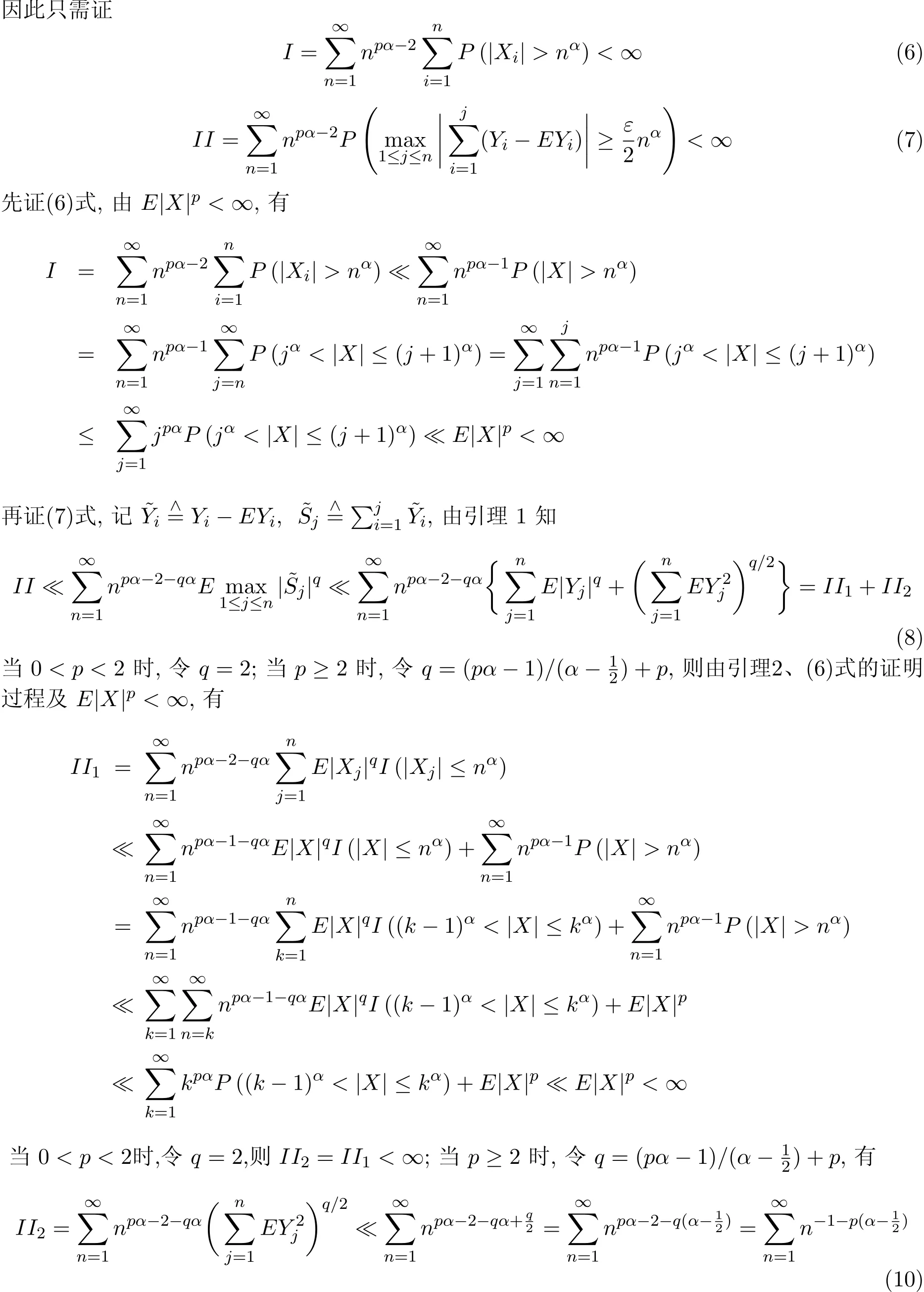
[1]Bradley R C.Equivalent Mixing Conditions for Random Fields[M].Chapel Hill:Univ of North Carolina, 1990.

[2]Bryc W,Smolenski W.Moment conditions for almost sure convergence of weakly correlated random variables[J].Proceeding of American Math Society,1993,119:629-635.

[3]Utev S,Peligrad M.Maximal inequalities and an invariance principle for a class of weakly dependent random variables[J].Theoret Probab,2003,16,101-115.

[4]杨善朝.一类随机变量部分和的矩不等式及其应用[J].科学通报,1998,43(17):1823-1827.

[5]吴群英.不同分布˜ρ混合序列的强收敛速度[J].数学研究与评论,2004,24(1):173-179.

[6]吴群英.˜ρ混合序列的若干收敛性质[J].工程数学学报,2001,18(3):58-64,50

[7]吴群英.˜ρ混合序列加权和的完全收敛性和强收敛性[J].应用数学,2002,15(1):1-4.

[8]吴群英.˜ρ混合序列的不变原理[J].纯粹数学与应用数学,2003,19(1):12-15.

[9]刘筱萍.不同分布˜ρ混合序列的完全收敛性[J].桂林工学院学报,2006,26(2):298-301

[10]冯凤香.不同分布˜ρ混合序列加权和的完全收敛性和强收敛性[J].桂林工学院学报,2008，28(2):282-284

[11]蔡光辉,郭宝才.˜ρ混合序列的对数律和强大数律[J].科技通报2006，22(3):288-291.

[12]吴群英.混合序列的概率极限理论[M].北京:科学出版社,2006.

Strong law of large numbers for˜ρ mixing random sequences

FENG Feng-xiang
(school of science,Guilin University of Technology,Guilin541004,China)

In this paper,the complete convergence and the sum’s strong convergence of different distributed˜ρ mixing random sequences were disscussed.We obtained the same results as independent sequences by moment inequality and trunccating.

˜ρ mixing,complete convergence,strong convergence,moment condition

O211.4

A

1008-5513(2009)03-0534-07

2008-03-21.

国家自然科学基金(10661006),广西教育厅科研项目(200807LX188).

冯凤香(1975-),硕士,讲师,研究方向：概率极限理论.

2000MSC:60F15