可靠度的M-Bayes可信限

唐燕贞,韩明

(1.福建师范大学数学与计算机科学学院,福建福州 350007;2.福建工程学院数理系,福建福州 350108)

可靠度的M-Bayes可信限

唐燕贞1,2,韩明2

(1.福建师范大学数学与计算机科学学院,福建福州 350007;2.福建工程学院数理系,福建福州 350108)

在可靠性试验中,有时会出现无失效数据,特别是在高可靠性、小样本试验中更容易产生无失效数据.本文提出了无失效数据情形,产品可靠度的一种新的参数估计方法–“M-Bayes可信限法”,给出了产品可靠度的M-Bayes可信下限的定义和M-Bayes可信下限的估计公式,并给出了M-Bayes可信下限估计的性质.最后,给出了数值算例,通过例子可以看出,本文提出的方法可行且便于应用.

可靠度;无失效数据;M-Bayes可信限;经典置信限

1 引言

对一些高可靠性产品,要想获得其失效数据,不但要花费很长的试验时间,而且对价格昂贵产品的破坏性也是令人难以忍受的.随着科学技术的发展,产品的可靠性不断提高,高可靠性产品在定时截尾可靠性试验中经常出现无失效数据.无失效数据问题的研究,对于建立在失效数据基础上的现有可靠性理论来说,是一个有一定难度的问题.自从文[1]发表以来,对无失效数据问题的研究逐渐引起了国内外的重视,并且已取得了一些成果.关于无失效数据问题的若干研究进展情况,见文[2-3].

在有些情况下,很难确定产品的寿命分布类型,有时虽然产品的寿命分布类型已知,但获得的数据仅仅是失效个数,而无精确的失效时间,这时我们可以借助非参数方法来获得可靠度的估计.设某产品的寿命分布类型是未知的,现从中随机抽取n个样品进行定时截尾试验,若在截尾时间段内有X个样品失效,又产品的失效与否是互相独立的,则X是一个服从二项分布的随机变量,于是有

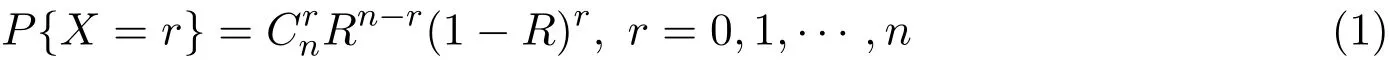
其中0＜R＜1,R为产品的可靠度.

这样研究可靠度的非参数估计问题,就转化为研究二项分布(1)式中参数R的估计问题.关于参数估计,近年来用Bayes方法取得了一些进展.特别是在文献[4]中提出了多层先验分布的想法以来,Bayes方法和多层Bayes方法在无失效数据的处理上取得了一些进展.在文[5]中,对二项分布,给出了一种Bayes估计.在文[6]中,对二项分布无失效数据情形,给出了可靠度的多层Bayes估计.

2 可靠度的M-Bayes可信限

2.1 R的M-Bayes可信限的定义

若R的先验分布为幂分布,其密度函数为

2.2 R的M-Bayes可信限的估计

以上在定义1中给出了R的M-Bayes可信下限的定义,以下将在这个定义的基础上给出R的MBayes可信下限的估计.

定理1对二项分布(1)式,在无失效数据情况下,若R的先验密度函数π(R|a)由(2)式给出,则有:

3 可靠度的M-Bayes可信限的性质

为了给出可靠度的M-Bayes可信限的性质–可靠度的M-Bayes可信下限与经典置信下限的关系,以下先给出可靠度的经典置信下限.

3.1 可靠度的经典置信下限

在文[7]中,给出了无失效数据情况下,R的置信水平为1−α(0＜α＜1)的经典置信下限的估计,现在叙述在如下的定理2中.

3.2 可靠度的M-Bayes可信下限与经典置信下限的关系

在定理1和定理2中分别给出了可靠度的M-Bayes可信下限与经典置信下限,那么它们之间有什么关系呢?以下将要给出的定理3回答了这个问题.

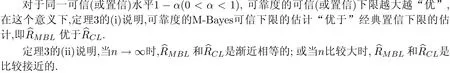
4 数值算例

当α=0.05,0.10,0.15,0.20,0.25,0.30和n=5,10,20,50,100时,根据定理1和定理2,可以得到可靠度的可信水平为1−α的M-Bayes可信下限的估计、置信水平为1−α的经典置信下限的估计,其计算结果见表1–5.

表1和的计算结果(n=5)

表1和的计算结果(n=5)

α 0.050.100.150.200.250.30 ˆRCL0.549 2800.630 9570.684 2550.724 7800.757 8580.786 003 ˆRMBL0.580 0280.657 9330.708 2690.746 3020.777 2030.803 399 ˆRMBL−ˆRCL0.030 7480.026 9760.024 0140.021 5220.019 3450.017 396

表2和的计算结果(n=10)

表2和的计算结果(n=10)

α 0.050.100.150.200.250.30 ˆRCL0.741 1340.794 3280.827 1970.851 3400.870 5510.886 568 ˆRMBL0.751 7830.803 0860.834 7040.857 8900.876 3160.891 666 ˆRMBL−ˆRCL0.010 6490.008 7580.007 5070.006 5500.005 7650.005 098

表3 ˆRMBL和ˆRCL的计算结果(n=20)

表4和的计算结果(n=50)

表4和的计算结果(n=50)

α 0.050.100.150.200.250.30 ˆRCL0.941 8450.954 9930.962 7680.968 3240.972 6550.976 208 ˆRMBL0.942 4040.955 4280.963 1300.968 6320.972 9220.976 441 ˆRMBL−ˆRCL0.000 5590.000 4350.000 3620.000 3080.000 2670.000 233

表5和的计算结果(n=100)

表5和的计算结果(n=100)

α 0.050.100.150.200.250.30 ˆRCL0.970 4870.977 2370.981 2080.984 0340.986 2330.988 032 ˆRMBL0.970 6320.977 3490.981 3000.984 1130.986 3010.988 092 ˆRMBL−ˆRCL0.000 1450.000 1120.000 0920.000 0790.000 0680.000 060

5 结束语

本文给出了可靠度的M-Bayes可信下限的定义(定义1),在此基础上给出了可靠度的MBayes可信下限的估计(定理1)与经典置信下限的估计(定理2),并给出了可靠度的M-Bayes可信限的性质(定理3).从数值算例可以看出,对于同一可信(或置信)水平,可靠度的M-Bayes可信下限的估计“优于”经典置信下限的估计,但随着n的增加,这种“优于”性逐渐减小.从数值算例还可以看出,本文提出的方法可行且便于应用.

[1]Martz H F,Waller R A.A Bayesian zero-failure(BAZE)reliability demonstration testing procedure[J]. Journal of Quality Technology,1979,11(3):128-137.

[4]韩明.无失效数据可靠性进展[J].数学进展,2002,31(1):7-19.

[3]韩明.基于无失效数据的可靠性参数估计[M].北京:中国统计出版社,2005.

[4]Lindley D V,Smith A F M.Bayes estimaters for the linear model[J].Journal of the Royal Statistical Society, Series B,1972,34:1-41.

[5]Miller K W,Morell L J,Noonan R E,et al.Estimating the probability of failure when testing reveals no failures[J].IEEE Trans,on Software Engineering.1992,18(1):33-43.

[6]韩明.Estimation of reliability based on zero-failure data[J].纯粹数学与应用数学,2002,18(2):165-169.

[7]韩明,赵任杰.成败型无失效数据的可靠性分析[J].信息工程学院学报,1992,11(3):27-35.

M-Bayesian credible limit of reliability

TANG Yan-zhen1,2,HAN Ming2
(1.School of Mathematics and Computer Science,Fujian Normal University,Fuzhou350007,China; 2.Department of Mathematics and Physics,Fujian University of Technology,Fuzhou350108,China)

For high reliability products,zero-failure data situation happens sometimes in the reliability tests, eapecially in high reliability and small sample tests.In this paper,introduces a new parameter estimation method—M-Bayesian credible limit method,in zero-failure data situation.The definition,formula and properties of the M-Bayesian credible lower limit for reliability are given.Finally,example is given.Through the example show that the provided method is feasible and easy to perform.

reliability,zero-failure data,M-Bayesian credible limit,classics confidence limit

O213.2

A

1008-5513(2009)03-0521-05

2007-06-21.

福建省自然科学基金(2009J01001).

唐燕贞(1974-),讲师,在职研究生,研究方向：数理统计及其应用.

2000MSC:62N05,62F15