与直径和围长有关的图的最大亏格
2009-07-05刘端凤黄元秋阳宁光
刘端凤,黄元秋,阳宁光
(1.广东工业大学应用数学学院,广东广州 510006;2.湖南师范大学数学与计算机科学学院,湖南长沙 410081;3.广东商学院数学与计算科学学院,广东广州 510320)
与直径和围长有关的图的最大亏格
刘端凤1,黄元秋2,阳宁光3
(1.广东工业大学应用数学学院,广东广州 510006;2.湖南师范大学数学与计算机科学学院,湖南长沙 410081;3.广东商学院数学与计算科学学院,广东广州 510320)
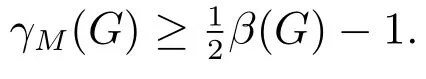
直径;Betti亏数;上可嵌入的;最大亏格
1 引言

定理A设G为图,
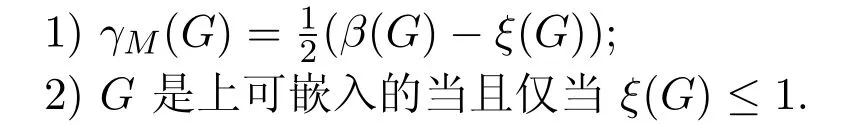
设A⊆E(G)为图G的一个边子集,记号c(GX)表示GX的所有连通分支个数;而记号b(GX)表示具有圈秩数为奇数的GX的所有连通分支个数.对于图G的任意点集X,X关于G的点导出子图是以X为点集且以两个端点均在X中的边为边集的G的子图.文[4]给出了图G的ξ(G)另外一个组合表达式:
最大亏格和亏格是图的两个重要拓扑参数.研究图的最大亏格的下界与图的其它参数的关系一直是拓扑图论中引人关注的问题.结合一个或多个参数:比如说点的最小度[5]和直径,许多文献都给出了一系列图的最大亏格的下界.特别地,关于图的直径与最大亏格下界的关系,近年来引起了图论学者的重视.首先,文[6-8]分别考虑了直径为2,3,4的情形,得到了一些很有意义的结果.文[9]在此基础上,得到了如下结果:
结果1设G是直径为d的简单图,若G的围长也为d,则ξ(G)≤1,即图G是上可嵌入的,其中d为不小于4的偶数.
下面我们将用例子来说明,这个结果是错误的.
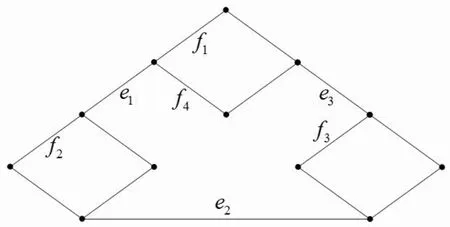
图1 G1以及它的一个平面嵌入
在G1中,取A={e1,e2,e3},这里A⊆E(G1),由定理B,容易得到ξ(G1)≥{c(GA)+ b(GA)−|A|−1}=3+3−3−1=2,取T为G1的一棵树,其中E(T)={E(G1)(f1,f2,f3,f4)}, V(T)=V(G1),此时ξ(G1,T)=2,由Betti亏数的定义知,ξ(G1)≤2,故ξ(G1)=2.从而说明结果1是错误的.文[9]的第二个结果:
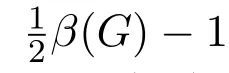
在说明它的证明过程之前,我们要先给出一个引理.关于一个非上可嵌入图,最近文[10]得到了如下结果:
引理1设G为图,若ξ(G)≥2,即G不是上可嵌入的,则存在G的边子集A,满足下列性质:
1)c(GA)≥2,且对GA的任意连通分支F,有β(F)≡1(mod 2);
2)对GA的任意连通分支F,F是G的点导出子图;
3)对GA的任意k(≥2)个不同连通分支F1,F2,…,Fk,则有|EG(F1,F2,…,Fk)|≤2k
−3;特别地,当k=2时,|EG(F1,F2)|≤1; 4)ξ(G)=2c(GA)−|A|−1.下面是文[9]中结果2的证明.
结果2的证明若G是上可嵌入的,即ξ(G)≤1,则结论显然成立.由文[7]知,d=3时,结论也成立.因此以下总假定G的直径d≥4,并且不是上可嵌入的,即ξ(G)≥2.由引理1 知,存在G的边子集A使得GA满足引理1的所有性质1)-4).
下面分三种情形来讨论:
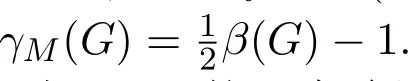
情形3若GA的连通分支数不少于4,设F1,F2,F3,F4为GA的任意4个连通分支,则它们中任何两个连通分支均有一条边相连(若不然,就会出现距离大于d的两个顶点).此时有|E(F1,F2,F3,F4)|=6,这与引理1性质3)|E(F1,F2,F3,F4)|≤2×4−3=5,矛盾.由情形3的证明过程可知,GA的连通分支个数不可能大于或等于4.但是我们可以找到具体的图来说明这时候GA的连通分支个数是可以大于或等于4的.

图2 G2以及它的一个平面嵌入
很明显,在G2中,G2A的连通分支个数为4.但是,此时我们取A={e1,e2,e3,e4,e5},这里A⊆E(G2),由定理B,容易得到ξ(G2)≥{c(GA)+b(GA)−|A|−1}=4+4−5−1=2,取T 为G2的一棵树,其中E(T)={E(G2)(e1,f1,f4,e2,f2,f3)},V(T)=V(G2),此时ξ(G2,T)= 2,由Betti亏数的定义知,ξ(G2)≤2.故ξ(G2)=2.也就说明了文[9]的证明过程是不严谨的.
下面我们给出正确的结果并证明之.
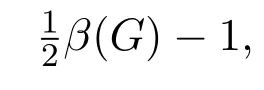
2 定理的证明
若G是上可嵌入的,即ξ(G)≤1,则结论显然成立.由文[6]知,d=3时,结论也成立.因此以下总假定G的直径d≥4,并且不是上可嵌入的,即ξ(G)≥2.由引理1知,存在G的边子集A使得GA满足引理1的所有性质.下面我们约定如下记号:
对任意集合X,|X|表示X的基数;
用ψ表示GA的所有连通分支组成的集合,此时为了方便我们把ψ中的元素与GA的连通分支无区别地看待;

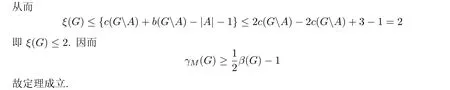
由定理的证明过程易知,若将定理的条件“G的围长为d”改为“G的围长不小于d”,而其他条件不变,其结论仍然成立.
注文中图1和图2同时说明了定理中关于γM(G)的下界也是最好的.
[1]Bondy J A,M urty U SR.G raph Theory with App lication[M].London:M acm illan,1976.
[2]Nordhaus E,Stewart B,W hite A.On the maximum genus of a graph[J].J.Combinatorial Theory B, 1971,11:258-267.
[3]刘彦佩.图的可嵌入性理论[M].北京:科学出版社,1994.
[4]Nebesky L.A new characterization of them aximum of a graph[J].J.Czechoslovak M ath.,1981,31(106):604-613.
[5]苏本堂,苗莲英.最小度和[a,b]-因子[J].纯粹数学与应用数学,2003,19(4):63-66
[6]Skoviera M.Them aximum genus of graph s of diam eter two[J].Discrete Mathem atics,1991,87:175-180.
[7]Hunglin Fu,minchu Tsai.Themaximum genus of diameter three graphs[J].Australasian JCombinato-rics, 1996,14:187-197.
[8]黄元秋,刘彦佩.关于直径为4的图的最大亏格[J].数学物理学报:A,2001,21(3):349-354.
[9]盛秀艳.与直径和围长有关的最大亏格的下界[J].数学学报,2004,47(6):1201-1204.
[10]黄元秋,刘彦佩.图的上可嵌入性[J].中国科学:A辑,1998,28(3):223-228.
(1.Departm ent of App lied Mathem atics,Guangdong University of Technology,Guangzhou 510006,China; 2.Department of Mathematics and Com puter Science,Hunan Normal University,Changsha 410081,China; 3.Departm ent of Mathem atics and Com puter Science,Guangdong University of Business Studies, Guangzhou 510320,China)
The maximum genus on graphs in terms of diameter and girth
LIU Duan-feng1,HUANG Yuan-qiu2,YANG Ning-guang3

diam eter,Betti deficiency number,upper embeddab le,m aximum genus 2000M SC:05C
O157.5
A
1008-5513(2009)02-0284-05
2007-12-10.
国家自然科学基金(10771062),教育部新世纪优秀人才支持项目(NCET-07-0276),广东工业大学校青年基金(062060).
刘端凤(1976-),在读博士,讲师,研究方向:图论及其应用和计算机辅助几何设计.
