某类线性微分方程亚纯解的增长性

陈玉

(江西师范大学数学与信息科学学院,江西南昌 330022)

某类线性微分方程亚纯解的增长性

陈玉

(江西师范大学数学与信息科学学院,江西南昌 330022)

研究了一类亚纯函数系数的线性微分方程的解的增长性问题,得到了齐次和非齐线性微分方程亚纯解的增长级、超级、二级不同零点收敛指数的精确估计.

线性微分方程；亚纯解；超级；二级收敛指数

1 引言与结果

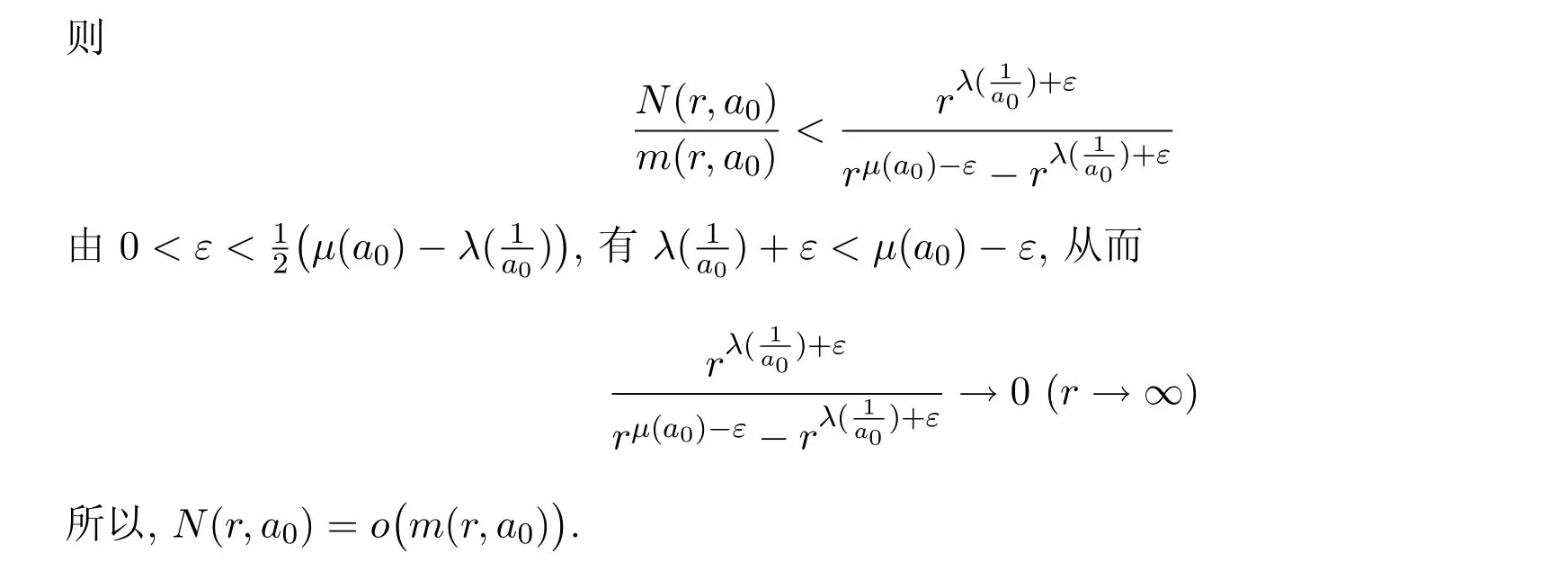
一个自然的问题是：当对方程解的性质起主要支配作用的系数a0为具有更多极点的亚纯函数时,如何估计微分方程解的增长性?本文研究了此问题,在更一般的条件下估计了某类线性微分方程的亚纯解的增长性问题,用超级、二级零点收敛指数的概念进一步精确地估计了微分方程的无穷级解的增长率、零点密度,得到以下结果.

2 定理1证明所需引理

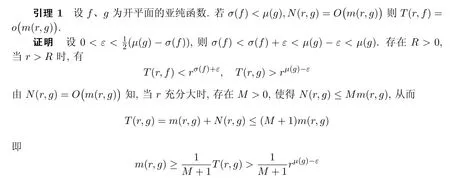
3 定理1的证明

4 定理2证明所需引理

5 定理2的证明

[1]Haym an W.M erom orphic Functions[M].Oxford:C larendon Press,1964.

[2]杨乐.值分布论及其新研究[M].北京:科学出版社,1982.

[3]何育赞,萧修治.代数体函数与常微分方程[M].北京:科学出版社,1988.

[4]仪洪勋,杨重骏.亚纯函数唯一性理论[M].北京:科学出版社,1995.

[5]陈宗煊.二阶复域微分方程解的不动点与超级[J].数学物理学报,2000,20(3):425-432.

[6]陈宗煊.关于高阶线性微分方程亚纯解的增长率[J].数学学报,1999,42(3):551-558.

[7]陈宗煊.二阶亚纯系数微分方程亚纯解的零点[J].数学物理学报,1996,16(3):276-283.

[8]高仕安,陈宗煊,陈特为.线性微分方程的复振荡理论[M].武昌:华中理工大学出版社,1997.

[9]Chen Zongxuan,Yang Chungchun.Quantitative estimations on the zeros and grow ths of entire solutions of linear differential equations[J].Com p lex Variables,2000,42:119-133.

On the growth of merom orphic solutions of a class of linear differential equations

CHEN Yu

(Institute of Mathem atics and In form atics,Jiangxi Norm al University,Nanchang 330022,China)

Studying the properties of grow th of solutions of a class of linear differential equationswith merom orphic coefficients,and obtain some p recise estim ates of the order of grow th,the hyper-order and the hyperexponent of convergence of sequence of distinct zeros of hom ogeneous and non-homogeneous linear differential equations.

linear differential equation,m erom orphic solutions,hyper-order,hyper-exponent of convergence

O174.52

A

1008-5513(2009)02-0261-07

2007-07-27.

江西省教育厅科学技术研究项目(赣教技字[2007]135).

陈玉(1973-),讲师,研究方向：复分析.

2000M SC:30D 35