中国城镇居民收入和消费的灰色预测*

詹锦华

（仰恩大学经济学院，福建泉州361024）

中国城镇居民收入和消费的灰色预测*

詹锦华

（仰恩大学经济学院，福建泉州361024）

根据2000—2007年中国城镇居民家庭人均可支配收入和人均生活消费数据，运用灰色预测模型对2008—2015年中国城镇居民的可支配收入和生活消费进行预测；结果表明，模型精度高，预测结果可信度强。预测结果表明，城镇居民整体可支配收入和消费水平呈现同方向的增长，但后者占前者的比例呈现小幅下降的趋势。

灰色系统；城镇居民；可支配收入；消费

我国城镇居民收入的提高和消费的扩大对于促进我国城镇经济可持续发展具有重要的意义。消费作为总需求的重要组成部分，是宏观经济调控的一个基本变量，而收入是决定消费的最基本因素。因而，对中国城镇居民收入和消费的走势进行预测，对国家制定宏观经济政策具有重要的意义。灰色系统理论，是一种研究少数据、贫信息不确定性问题的方法。该理论以“部分信息已知和部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，通过对“部分已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控”[1]。社会经济系统，由于其没有明确的“内”、“外”关系，系统本身与系统环境、系统内部与系统外部的边界若明若暗，因而，用灰色系统理论对其进行研究能够得到很好的效果（如王英，刘思峰采用灰色理论较好地预测了我国对外直接投资规模[2]）。本文将采用灰预测方法对我国城镇居民收入和消费进行预测。

一、灰色预测模型

（一）灰色预测模型GM(1,1)

灰色预测模型GM（Grey Model）包括一阶单变量的GM（1,1）模型和n阶h个变量的GM（n,h）模型[3]，它兼有微分方程、差分方程和指数方程的特性。本文采用最常用的GM(1,1)模型。

设X（0）为GM(1,1)的建模序列，X（0）={X（0）（1），X（0）（2），…，X（0）（n）}，令X（1）为X（0）的一次累加生成序列，令相应的微分方程为：

常数项矩阵Yn=[X（0）（2），X（0）（3），…，X（0）（n）]T

用最小二乘法求解α∧=(BTB)-1BTYn=［αμ］

求微分方程的时间函数：

累减生成预测值：

X'（0）(k+1)=X'（1）(k+1)-X'（1）(k),X'（0）(1)=X'（1）(1)

(二)GM(1,1)模型检验

1.事前检验

事前检验是对原始数据序列X（0）作GM(1,1)建模的可行检验。当级比值落在可容区为(e-2，e2)内，即σ（0）(k)∈(0.1353，7.389)，表明X（0）是光滑的，可作灰预测。若则可获得精度较高的GM(1,1)模型。当灰发展系数-α≤0.3，GM(1，1)模型可以用于中长期预测。

2.事中检验

事中检验是对GM(1,1)模型的精度检验，一般采用残差检验、后验差检验、级比偏差值检验。

（1）残差检验。绝对残差Δ(0)=X(0)(k)-X'(0)(k)，相对残差平均精度p°=(1-ε(avg))×100%。一般要求ε(k)＜20%，最好是ε(k)＜10%；同时要求p°〉80%，最好是p°〉90%。

（2）后验差检验。原始序列的标准差：

绝对残差序列的标准差：

一般要求0.80＜P＜0.95,0.35＜C＜0.5,最好是P〉0.95,C＜0.35。

（3）级比偏差值检验。级比偏差为：

=1-uσ(0)(k)×100%

一般要求ρ(k)＜20%，最好是ρ(k)＜10%。

3.事后检验

事后检验即预测检验。一般可采用滚动检验。X(0)为原始序列，Xi(0)为建模序列X(0)的4维新陈代谢子列。如X4(0)={X(0)(1),X(0)(2),X(0)(3),X(0)(4)}，X5(0)={X(0)(2), X(0)(3)X(0)(4),X(0)(5)}…对Xi(0)作GM(1,1)建模。

平均滚动精度：p°run(avg)=(1-εrun(avg))×100%

一般要求p°run〉80%，最好是p°run〉90%。

(三)新陈代谢GM(1,1)模型

为了充分利用新信息的作用，进一步提高精度，可以建立新陈代谢GM(1,1)模型，即由已经建立的GM(1,1)模型，预测一个值，补充到已知序列中，同时去掉一个最老的信息，如此增加新信息去掉旧信息[4]。

根据以上建模思想方法和表1数据资料，分别建立我国城镇居民收入和消费的灰色预测模型。

表12000 —2007年中国城镇居民家庭平均每人可支配收入和生活消费支出/元

二、我国城镇居民家庭人均可支配收入GM(1,1)模型的导出及检验

（一）收入GM(1,1)模型的导出

设2000 2007年人均可支配收入数据为原始序列X(0)={6280.0，6859.6，7702.8，8472.2，9421.6，10493.0，11759.5，13786}，生成新序列X(1)={6280.0，13139.6，20842.4，29314.6，38736.2，49229.2，60988. 7，74774.7}，均值序列Z(1)={9709.8，16991，25078.5， 34025.4，43982.7，55108.95，67881.7}。根据GM(1,1)

（二）收入GM(1,1)模型检验[5]

1.事前检验

级比σ(0)={0.916，0.891，0.909，0.899，0.898，即界区为(0.801，1.249)。级比都落在界区内，因此采用GM (1,1)模型且可获得精度较高的模型。灰发展系数-α=0.115412＜0.3，可以进行中长期预测。

2.事中检验

根据式（3）计算人均可支配收入预测序列X'(1)，X'(0)，进一步得到绝对残差Δ(0)(k)和相对残差ε (k)(见表2)。从表2中可以看出，ε(k)＜10%，ε(avg)= 1.567%＜5%，p0=98.433%〉90%。

表2 城镇居民可支配收入残差检验精度表

进行后验差检验：

由于S0=0.6745S1=1727.30，而Δ(0)(i)Δ(0)=｛22.64，114.40，135.19，18.42，104.96，196.23，234.63，-327.32｝各个值均小于S0，所以小误差概率P=1〉0.95，通过后验差检验。

由ρ(k)=1-μσ(0)(k)得：ρ=｛-0.02819，-0.00013，-0.02033，-0.00911，-0.00799，-0.00125，0.064974｝，可以看出各级比偏差值ρ(k)＜10%，模型精度好，通过级比偏差检验。

3.事后检验

用X4(0)={X(0)(1),X(0)(2),X(0)(3),X(0)(4)}建模得预测值X'(0)(5)=9423.33；用X5(0)={X(0)(2),X(0)(3)X(0)(4),X(0)(5)}建模得预测值X'(0)(6)=10396.16；用X6(0)={X(0)(3)X(0)(4),X(0)(5),X(0)(6)}建模得预测值X'(0)(7)=111660.52；同理可得，X8'(0)=13111.11。进而可得：εrun(5)=-0.0002，εrun(6)=-0.0092，εrun(7)=-0.0084，εrun(8)=-0.0490， εrun(avg)=1.67%,=98.33%〉90%，预测模型具有98.33%的可信程度。

三、我国城镇居民消费GM(1,1)模型的导出及检验

（一）消费GM(1,1)模型的导出

根据2000 2007年消费数据和GM(1,1)模型建立方法，求得确定白化模型方程为：

依据式（2）确定时间响应式为：

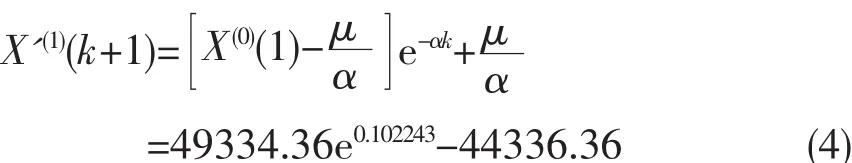
(二)消费GM(1,1)模型检验

1.事前检验

级比σ(0)={0.941，0.880，0.926，0.907，0.904，0.913，0.870}，级比都落在界区内，可以采用GM(1,1)模型且可获得精度较高的模型。灰发展系数α= 0.102243＜0.3，可以进行中长期预测。

2.事中检验

根据式（4）计算人均可支配收入预测序列X'(1)和X'(0)，进一步可得Δ(0)(k)ε(k)（见表3）。

表3 城镇居民家庭平均每人消费支出的残差检验

从而ε(k)＜10%，ε(avg)=1.058%＜5%，p°= 98.942%〉90%，通过残差检验。

S1=1722.74,小误差概率P=1〉0.95，通过后验差检验。

由得ρ(k)=1-μσ(0)(k)得:ρ=｛-0.0429，0.0247，-0.0259，-0.0042，-0.0017，-0.0118，0.0364｝，可以看出各级比偏差值ρ(k)＜10%，模型精度好，通过级比偏差检验。

3.事后检验

由4维子序列预测，可得：X'(0)(5)=7239.97,X'(0)(6)=7813.32,X'(0)(7)=8760.86,X'(0)(8)=9570.13。εrun(5) =-0.0081，εrun(6)=0.0163，εrun(7)=0.0074，εrun(8)=-0.0427，εrun(avg)=1.86%,=98.14%〉90%，预测模型具有很好的可信程度。

四、基于GM(1,1)模型的城镇居民家庭人均可支配收入和生活消费支出预测

上述检验表明GM(1,1)模型具有相当好的精度，因此可利用式（3）和式（4）对2008 2015年我国城镇居民家庭人均可支配收入和生活消费支出分别进行预测。为充分体现新信息的作用，在上述GM(1,1)模型基础上，分别建立了收入和消费的八维新陈代谢GM(1,1)模型群，并对城镇居民家庭人均可支配收入和生活消费进行预测[7]。预测结果列于表4中。

表42008 —2015年中国城镇居民家庭人均可支配收入和生活消费支出预测/元

图1 2000—2015年城镇居民人均可支配收入GM(1,1)预测值和实际值

图2 2000—2015年城镇居民生活消费基础GM(1,1)预测值和实际值

从图1和图2可知，2000 2007年我国城镇居民的模型计算值和实际吻合程度相当高，因此表明所建模型具有极高的可信度。2008 2015年期我国城镇居民的整体可支配收入和消费水平呈现同方向的增长。二者有密切联系。一方面，收入提高了，居民的生活水平也相应提高，因而消费水平随之增长。另一方面，消费增加了，必将拉动经济增长，从而增加城镇居民的可支配收入。此外，我们可以看到，2000 2015年城镇居民人均生活消费支出占可支配收入的比例呈现略微下降的趋势。2000年，城镇居民的生活消费支出占可支配收入的80%，2005占76%，2010年，占71%。到2015年，则减少到67%。本文分析这是由于我国处在经济和社会转型时期，理性的居民由于子女教育、失业和养老等方面的考虑，会将收入转化为足够的预防性储蓄。

五、结束语

根据事前、事中、事后检验可知，所建的模型具有很高精度，由此获得的预测结果可信度强，对中国城镇经济的发展具有很好的预测作用，能够为中国经济政策的制定提供可靠的参考依据。

此外，预测结果也表明我国城镇居民整体可支配收入和消费水平呈现同方向的增长，后者占前者的比例呈现小幅下降的趋势。因此我国在充分重视通过增加居民收入刺激消费的同时，也应注意建立和完善各种社会保障性制度，让居民减少顾虑、增加消费，以促进经济的繁荣、收入的增长，从而促进收入和消费的良性循环。

[1]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社, 2002:221-225.

[2]王英,刘思峰.基于灰色理论的我国对外直接规模预测[J].统计与决策,2008(13):79-81.

[3]邓聚龙.灰预测与灰决策[M].武汉:华中科技大学出版社,2002:99-105.

[4]刘思峰,郭天榜,党耀国.灰色理论及应用[M].北京:科学出版社,1999:117-118.

[5]相丽驰,金晓彤.中国农村居民“十一五”期间收入和消费的灰色预测[J].经济问题探索,2007(4):27-30.

[6]蒋满霖,周国霞.我国城镇居民收入和消费的协整分析[J].安徽工业大学学报,2006(3):80-82.

[7]徐国祥.统计预测和决策[M].上海财经大学出版社, 2005:208-209.

[8]牛飞亮.80年代中期以来中国城镇居民收入差距的来源结构分析[J].西北农林科技大学学报,2001,1(4):36-44.

[9]蒋云飞,罗守贵.改革开入以来中国城镇居民消费结构变动及区域差异[J].经济地理,2008,28(3):23-26.

[10]石建平.中国城镇居民恩格尔系数的灰色系统研究[J].甘肃金融,2008(14):15-18.

（责任编校：夏东、杨睿）

Grey prediction for China’s urban resident income and consumption

ZHAN Jin-hua
(School of Economics,Yangen University,Fujian Quanzhou 361024,China)

According to China’s urban resident family per capita disposable income and per capita living consumption data during 2000-2007,by using grey prediction model to predict China’s urban resident disposable income and living consumption during 2008-2015,the results show that models have higher accuracy and predicted results are believable.The results indicate that urban resident total disposable income and consumption level are growing in the same direction but proportion of the latter shows decreasing trends.

grey system;urban resident;disposable income;consumption

F224.9

A

1672－0598(2009)02-0042-05

10.3969/j.issn.1672-0598.2009.02.010

2009-01-14

詹锦华（1971－），女，福建建瓯人，讲师，经济学硕士，仰恩大学经济学院，从事跨国投资、农村经济研究。