浅议现代教育技术在中职数学课堂的应用

莫江文

[摘要]以现代教育技术为基点，从职业教育的实际出发，应用现代教育技术优化中职教学课堂教学，可促进学生有效学习，提高教学质量。

[关键词]现代教育技术职业技校数学教学

现代教育技术是运用各种理论及技术，通过对教与学过程及习惯资源的设计、开发、利用、管理和评价，实现教育教学优化的理论与实践。它集图、文、声、色、像于一体，化静态为动态。化抽象为直观。化难为易，把原来抽象、教师难以讲清、学生难以理解的教学内容变得直观具体、生动活泼和丰富多彩。在中职数学课堂应用现代教育技术教学，可促进学生有效学习，提高教学质量。

一、创设动态情景，渲染气氛，提高学生兴趣

著名教育学家苏霍姆林斯基说过：“如果教师不想方设法使学生进入情绪高昂和智力振奋状态，就急于传授，那么这种知识只能使人产生冷漠的态度，不动感情的脑力劳动就会带来疲倦。”兴趣是学习的强大动力。学生在即将学习新知识时，教师如果能根据教学内容，选用适当的教学手段，创设新奇的教学环境，就会激起学生积极探究新知识的兴趣。现代教育技术中，多媒体具有视听合一的功能与计算机的交互功能，二者结合可产生出一种新的图文并茂的、丰富多彩的人机交互方式。将其应用于中职教学课堂，可有效地激发学生的学习兴趣，使学生产生强烈的学习欲望，从而形成学习动机，实现教学导向功能。例如，等比数列一课的开始。教师可播放国王和大臣下棋的故事片，让学生边欣赏画面，边听配乐录音，结束后请学生讨论：大臣的要求能满足吗?大臣要的麦粒有多少?继而揭示课题。再如，在讲授《平面向量》的内容时，播放一段在海边纤夫拉船的电影片段，再配上歌曲《伏尔加河上的纤夫》，然后引入向量的定义。以“趣”引路，激发学生的学习欲望。

二、化静为动，降低难度，解决重点、难点问题

数学的教学内容与其他科目相比较为抽象，再加上有些内容以传统的教学手段讲授效果不佳，学生难以掌握，这就形成了教学的难点。而教学重点则是在教学过程中要求学生必须掌握的内容。传统的教学方法在某些教学重点、难点的教学上有一定的局限性。现代教育技术进入数学课堂，可使抽象的概念具体化、形象化。尤其是现代教育技术能进行动态的演示，弥补了传统教学方式在直观感、立体感和动态感等方面的不足。利用现代教育技术这一特点，可处理其他教学方法难以处理的问题，并能引起学生的兴趣，从而增强学生的直观印象，这就为教师解决教学难点、突破教学重点、提高课堂效率和教学效果提供了一种现代化的教学手段。“函数”是中职数学中最基本、最重要的概念，它的概念和思维方法渗透在中职数学的各个部分；同时，函数是以运动变化的观点对现实世界数量关系的一种刻画，这又决定了它是对学生进行素质教育的重要材料。为了解决数形结合的问题，在有关函数的传统教学中，教师多是手工绘图，但手工绘图具有不精确、速度慢的弊端，而应用几何画板快速直观的显示及变化功能则可以克服上述弊端，大大提高课堂效率，进而起到事半功倍的效果。教师可以用几何画板根据函数的解析式快速作出函数的图像，并在同一个坐标系中作出多个函数的图像。例如。在完成“指数函数Y=ax的图像和性质”这一教学内容时，其教学重点与难点是指数函数的图像及性质。采用几何画板，在学生任意确定a(a＞0且a)的大小后，指数函数的性质：都经过点(0，1)，图像都在x轴上方，对称性及单调性很快就可以在出现的函数图像上显示出来，并且显示是动态的。学生每输入一个数据，就显示一条动态的曲线，并且还可以显示经过的特殊点(0，1)，学生在同一个直角坐标系中作出若干个指数函数图像，比较各图像的形状和位置，很容易就能归纳指数函数的性质，解决了此节课内容的重点与难点。

三、展现过程，发展能力，把数学实验引入课堂

利用现代教育技术，设置数学实验室。在数学实验室里，学生从“听”数学的学习方式。变成在老师指导下的“做”数学，学生从过去被动地接受现成的数学知识，变成像数学家一样去“发现”数学知识，通过数学实验，学生可以理解数学问题的来龙去脉，以及它的发现、分析和解决过程，从感觉到理解，从具体到抽象，数学的抽象变得易于理解，数学的严谨变得合情合理。这种探索和发现的学习方式可以使学生更好的保持和理解数学知识，更加自信，更有助于学生思维。

例如：在完成《球的体积》计算公式时，需要通过等积变形，将球分割成无数个椎体来推导球的体积公式。以前教师运用教具很难较好地完成“由曲变直”，将现代教育技术应用于课堂之后，教师指点学生由计算机将球切割等分成32份、64份……甚至无限。球等分的过程具体、现象、清晰，突破了现实的局限，使学生在观察的过程中开启了心智，不仅掌握了球的体积公式，也掌握了求几何体体积可以采用切割的办法，也就是等体积求法。

教学实践发现，中职生解题能力一般较差，主要体现在理解能力和想象能力等方面。利用现代教育技术可以再现问题产生的经过，让学生难以解答的题目变得简单、明了，从而发展学生的认知能力。例如，一根棒AB长2米，斜靠在墙壁上，∠ABC=60°，如果棒的两端A、B分别沿AC、CB方向滑动至A'、B'，且AA'=(根号3-根号2)米，问棒的中点D随之运动至D'所经过的路程是多少(见图1)?

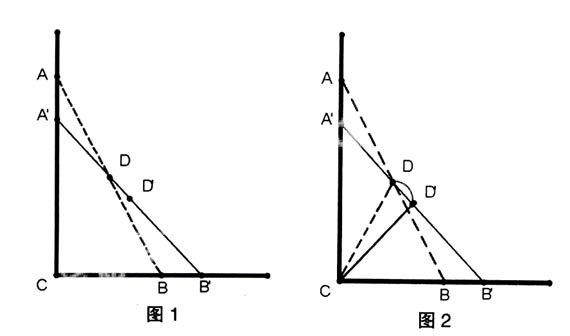
用多媒体辅助教学，教师预先做好一个几何画板的课件，把AB从LABC=60°到∠A'B'C'=45°做成动画，把D到D'做轨迹跟踪。题目展示后，学生稍作思考。教师则按动画按钮，轨迹马上就出现在眼前(见图2)。有了弧形，学生极易找到圆心、半径等，这样整道题目用多媒体辅助教学可使学生便于理解。

四、图文并茂，巧妙设问，激活思维

数学是思维的科学，思维从问题的开始，没有问题就没有思维。在数学教学中，练习是必不可少的。要使练习快速、有效，可根据学生思维过程及可能碰到的困难，运用多媒体技术巧妙设计一些灵活性、多样性和趣味性很强的练习、测试习题库及评估，再插入图片和文字，则可以省时，而且多变，并扩大联系容量，有利于激活学生的思维，培养分析问题和解决问题的能力。例如，在上到棱柱、棱锥等有关概念时，运用多媒体技术出现多种几何体，配上不同的颜色，出示有关问题。在学生回答正确时，屏幕上出现一个笑脸动画；答错时，给出一个哭脸动画；并要求学生重新思考，从而激发学生思维。

五、代替手工，准确画图，培养应用意识

学以致用是学习数学的目的之一，而图形计算机等现代教育手段的应用有利于学生应用意识的培养。

2004年全国数学高考题(江苏)第19题的题目是：制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损，某投资人打算投资甲、乙两个项目。根据预测，甲、乙项目可能的最大盈利率分别为100％和50％，可能的最大亏损率分别为30％和10％，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问：投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大?

这道题主要是考查学生对线性规划的应用能力，准确的画图是本体的解题关键。首先，应该设置变量，设投资人分别用x，y万元投资甲、乙两个项目，才能使盈利最大，其中目标函数为：z=x+0.5y，然后列出线性约束条件，然后列出限制条件：x+y≤10；0.3x+0.1y≤1.8；x≥0；y≥0。再画出可行域，最后在可行域中求出最大值。传统教学在黑板上画出各函数的图像后，画出可行域，但如果稍有不慎，画出的可行域不准确，就可能产生错解。往往要对几个解进行验算才能得出正确答案，而利用图形计算器就能快速而准确的画出可行域，从而准确地解答题目。

综上所述，运用现代教育技术，可让学生在视听中感受数学，在亲自操作中体验数学，实现师生互动、生生互动，活跃中职数学的课堂气氛，降低教学难度。使学生乐意并有更多的精力投入到现实的、探索性的数学活动中去。

(责编黎原)