重视情境教学 调动学生思维
2009-05-22杜修鹏
杜修鹏
数学的发展一再证明:“问题是数学的心脏。”这么说,数学的发展过程就是不断提出问题解决问题的过程。数学教育的核心是培养学生解决数学问题的能力。那么教师如何合理运用问题教学呢?创设问题情境,巧妙设置疑问,激发学生的认知潜能,实际上即为问题的提出、分析和解决的过程。在中学数学的教学中,情境教学因其能有效提高课堂效率,培养学生认知能力、主动学习能力、分析问题解决问题能力而倍受广大数学教师的钟爱。
一.对情景教学的理解
在实际问题的情景下,模仿数学家思维活动过程,挖掘数学认识动机、内在联系以及知识的产生和发展的情节为主体的教学手段是新课标要求下一种全新的教学模式。在运用这种教学方法的过程中必须注意以下几点:第一,构造思维活动的情节时,以探索启发为主不一定是遵守形式逻辑规则的严格思维,而是运用合理的推理和拟真推理进行教学;第二,设计教学活动过程必须联系学生的情感、意志、水平,使学生在兴奋状态下经历潜伏——存疑——豁然开朗的过程(也就是提出问题——试一试——不断尝试中增强信心)——下决心证明——得到正确结果的过程;第三,构成活动情节的类型有:(1)概念的形成过程;(2)方法的思考过程;(3)结果的探究过程。教学上应按这样的过程去设计教法,才能达到数学情境教学的目的。
二.实施情境教学的具体做法
数学情境教学的实施大致可以用如下框图进行:

下面就以勾股定理一课为例加以说明。
1.创设问题情境
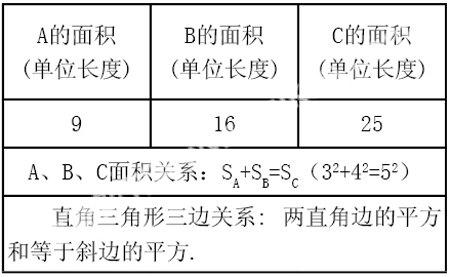
是指根据日常生活的实际问题、数学趣味问题等,挖掘出一个数学问题。如在讲授勾股定理时,设置问题情境:相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成地面中反映了直角三角形三边的某种数量关系。(出示图形)你能发现什么?
问题1:.A、B、C的面积有什么关系?
2.尝试学习
是指在教师的指导下,通过自己的尝试,探究问题的解决。尝试的目的是让学生自己动手动脑,以主动的姿态参与学习知识的全过程。学生通过观察可以得出结论。

结论1:SA+SB=SC
问题2:等腰直角三角形的三边之间有什么关系?(学生思考作答)
结论2:两直边的平方和等于斜边的平方。
3.深入探究
是指学生处于尝试学习的时候,可能会遇到一些疑问,为了帮助学生克服这些疑问,教师可以设置相关的问题,学生通过探究,得到新的结论。
问题3:任意一个直角三角形三边之间是否有上面的关系?(出示图形)

这时学生的思维又一次被调动起来,头脑处于兴奋状态,进入解决问题的高潮。
4.解决问题
这是情境教学的最后阶段,是整节课的高峰期。处于兴奋状态的学生自己动脑、动手去解决他们想解决而未解决的问题,因而思维特别活跃,对问题急于弄个水落石出。因而教师此时应用鼓励的目光和语言去帮助学生,使他们顺利解决问题。通过上面的探究过程,可得结论:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2
三.情境教学在数学教学中的意义
根据多年的教学情况看,使用情境教学法至少有如下好处:
1、数学情境教学一开始就提出了对全堂课起关键作用的、学生自己能够解决的、富有挑战性的问题,激发学生的浓厚学习兴趣并以积极的态度去解决所提出的问题,这就形成了“要求学习”的情境,为后面课的展开奠定了良好的基础。
2、创设了问题情境。问题是思维的出发点,有了问题才会去思考,对学生来说提出一些他们想解决而未解决的、富有挑战性、趣味性的问题更能激发学生的向心力,促使他们积极思考。
3、从实施过程来看,全体学生真正做到了动手、动脑、动口,积极参与教学的全过程,从不自觉到自觉地发挥了他们的思维能力和创造能力。
4、在教学中使以学生为主体教师为主导的教学原则得到了很好的贯彻。学生的学习是主动的学习,始终贯穿着学生的自主活动,充分发挥了学生在学习过程中的主体作用。让学生真正成为学习的主人,使他们去探索、去发现、去获取,其结果使教学系统中的教与学控制在最佳状态——学困生在练习中及时得到帮助,中等以上的学生也有进一步发挥的机会,从而教师更能从中了解学生的实际情况并及时调节教学环节。
5、数学情境教学重视发展学生的思维训练,能让学生越学越聪明。情境教学强调概念的形成过程、解题的分析思考过程和规律的揭示过程,常把学生的思维集中到问题的探索研究上来,就是连差生也容易想进去,学进去,从中尝到思考的乐趣。逐步爱上数学,真正做到把兴趣还给学生,把魅力还给数学。
6、数学情境教学重视调动学生的非智力因素,为学生建立了一个良好的心理环境。在学习中最活跃的成份是兴趣,而情境教学恰好提供了培养兴趣的基地。当学生解决了他们想解决而未解决的问题时,经教师的表扬会产生一种愉悦的心境,享受成功带来的快乐,这对培养学生对数学的兴趣毫无疑问是有积极意义的。
(作者联通:717300陕西省子长县齐家湾中学)