Modeling of Isomerization of C8 Aromatics by Online Least Squares Support Vector Machine*
2009-05-14LILijuan李丽娟SUHongye苏宏业andCHUJian褚建
LI Lijuan (李丽娟), SU Hongye (苏宏业) and CHU Jian (褚建)
Modeling of Isomerization of C8Aromatics by Online Least Squares Support Vector Machine*
LI Lijuan (李丽娟)1,2,**, SU Hongye (苏宏业)2and CHU Jian (褚建)2
1College of Automation and Electrical Engineering, Nanjing University of Technology, Nanjing 210009, China2State Key Lab. of Industrial Control Technology, Institute of Cyber-systems and Control, Zhejiang University, Hangzhou 310027, China
The least squares support vector regression (LS-SVR) is usually used for the modeling of single output system, but it is not well suitable for the actual multi-input-multi-output system. The paper aims at the modeling of multi-output systems by LS-SVR. The multi-output LS-SVR is derived in detail. To avoid the inversion of large matrix, the recursive algorithm of the parameters is given, which makes the online algorithm of LS-SVR practical. Since the computing time increases with the number of training samples, the sparseness is studied based on the projection of online LS-SVR. The residual of projection less than a threshold is omitted, so that a lot of samples are kept out of the training set and the sparseness is obtained. The standard LS-SVR, nonsparse online LS-SVR and sparse online LS-SVR with different threshold are used for modeling the isomerization of C8aromatics. The root-mean-square-error (RMSE), number of support vectors and running time of three algorithms are compared and the result indicates that the performance of sparse online LS-SVR is more favorable.
least squares support vector machine, multi-variable, online, sparseness, isomerization
1 Introduction
The C8aromatics fraction in a refinery consists mainly of four isomers,..,-xylene (OX),-xylene (MX),-xylene (PX) and ethylbenzene (EB). Of all these isomers, PX is the one with major industrial importance since it is widely used in the manufacture of synthetic fibers [1]. The isomers OX, MX and EB are converted into more valuable PX over the catalysts in the process of isomerization of C8aromatics [2].
Isomerization of C8aromatics is a multi-variable and highly complex process, the model of which has gained considerable interest over the years. Among the available literatures, kinetic models for different catalysts were widely studied [1-6]. However, the kinetic models varied with different operating conditions, and their precision was not so satisfactory for industrial process [2]. Some researchers attempted to model the isomerization process with data-driven model. Radial basis function-multidimension cyclic subspace regression (RBF-MCSR) method was applied in the isomerization of xylene and good performance was obtained [7]. An adaptive artificial neural network was applied in the modeling of aromatic hydrocarbon isomerization [8]. The statistical model was studied and the effects of different operating variables on the yield of-xylene were analyzed [1].
Support vector machine (SVM) [9, 10] has been used in classification and regression problems. Least squares support vector machine (LS-SVM) [11] is a modified version of SVM, in which analytical solutions can be obtained by solving linear equations instead of a quadratic programming (QP) problem. A good many of papers refer to the application of SVM in chemical engineering, such as polymerization process [12] and pure terephthalic acid (PTA) oxidation process [13, 14], which shows good performance of SVM in modeling of chemical industry.
In most modeling applications of LS-SVM, the output is single variable, which is not well suitable for the actual multi-input-multi-output system. In this paper, we present the multi-output least squares support vector regression (LS-SVR) and farther study the online algorithm. To avoid the inversion of large matrices in LS-SVM, the recursive formula and online LS-SVM have been presented [15]. Similarly, we propose the online LS-SVR for multi-output system in this study. The sparseness based on projection is discussed since the computing time increases rapidly with the number of samples. The presented online multi-output sparse algorithm is applied in the modeling of isomerization process of C8aromatics in a refinery. The accuracy and running time are compared for standard LS-SVR, nonsparse online LS-SVR and sparse online LS-SVR.
2 Multi-output least squares support vector regression
2.1 Standard least squares support vector regression
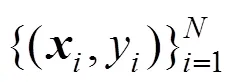

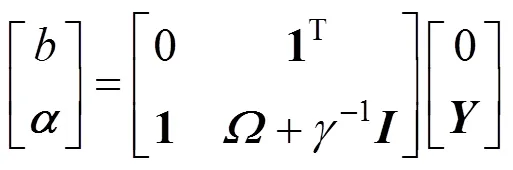
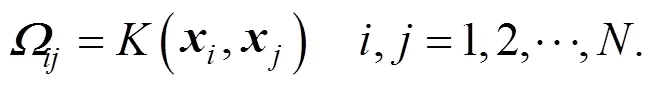
2.2 Multi-output least squares support vector regression

The optimization problem is defined as follows,

subjected to the equality constraints

The Lagrangian equation is defined as

which gives conditions for optimization,
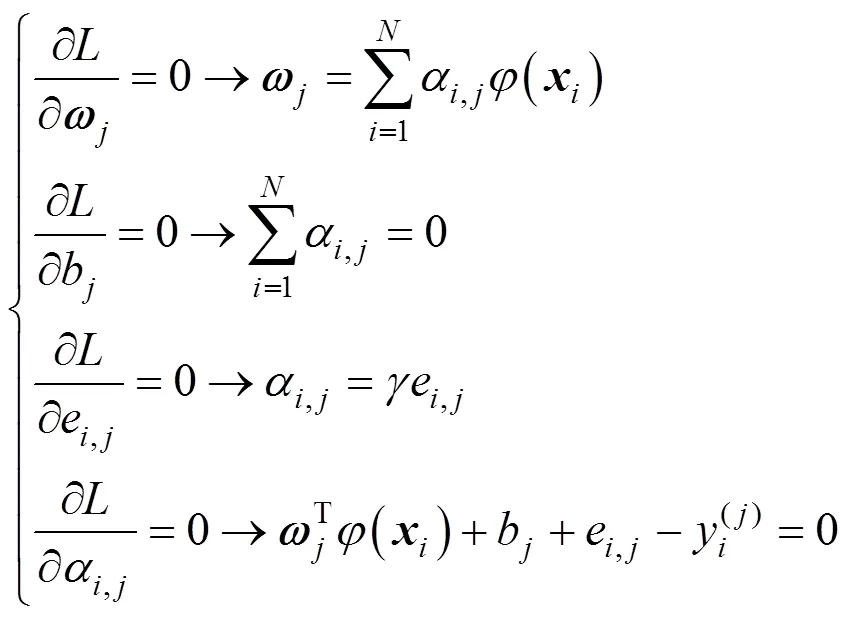


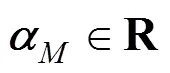

Then the LS-SVM model can be given by

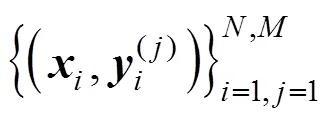
3 Online multi-output LS-SVR
3.1 Recursive algorithm of multi-output LS-SVR
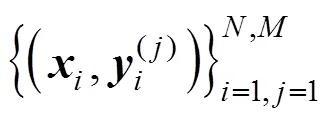
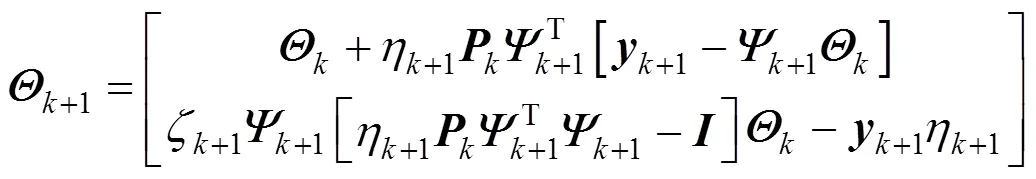

where


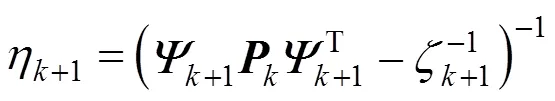
Proof We first introduce the following lemmas for convenience.
Lemma 1 Let,and (+) be nonsingular matrices, then
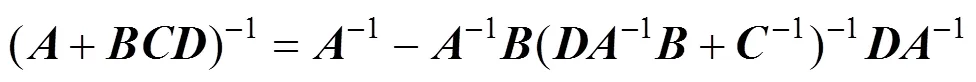
holds [17].
Lemma 2 Let partitioned matrix

and11,22be nonsingular matrices, then
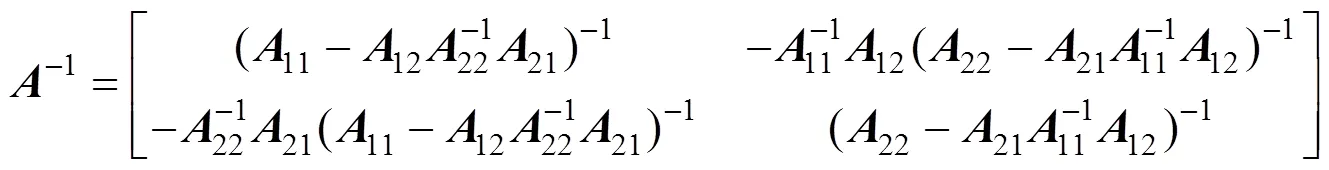
holds.
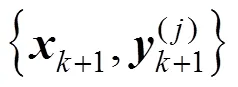
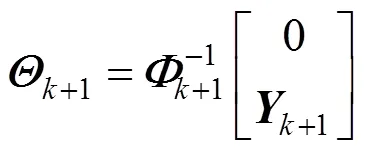

Assuming that
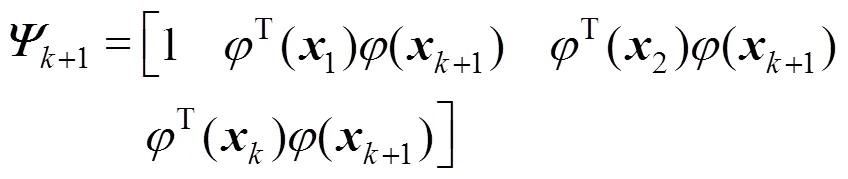
We can rewrite Eq. (18) as



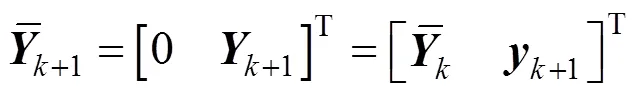
Eq. (17) can be written as follows,

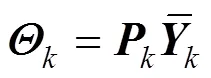

3.2 Sparsity of recursive algorithm
3.2.1

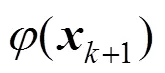

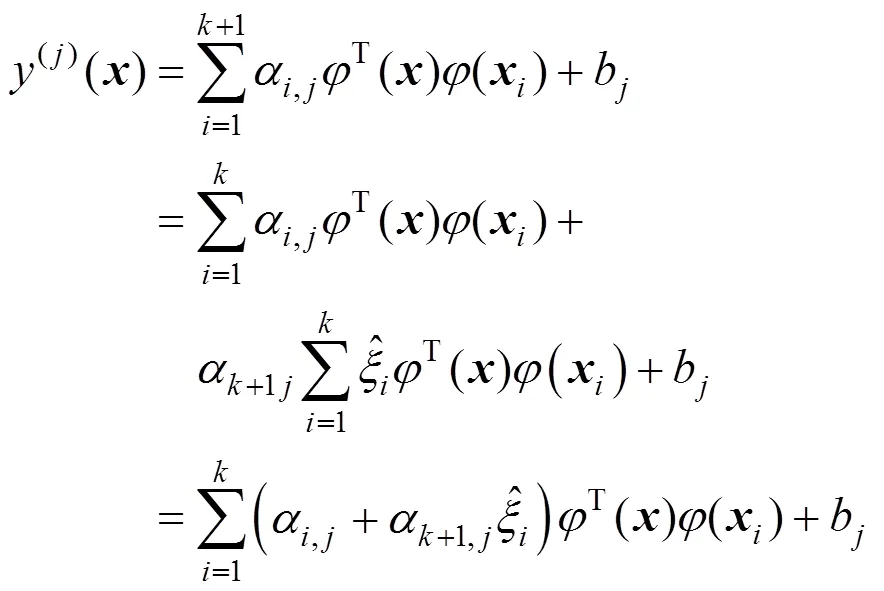
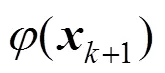
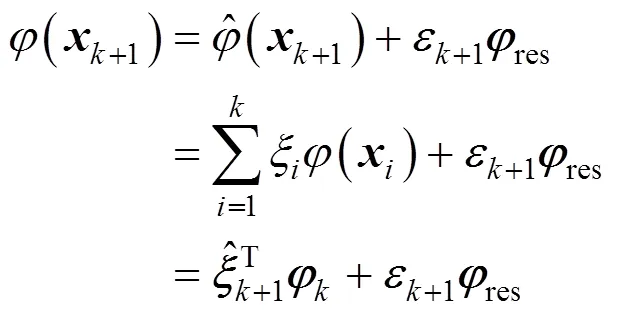
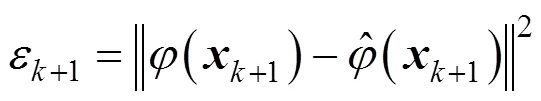
is the squared length of the residual.
3.2.2
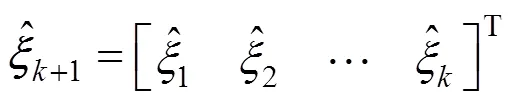


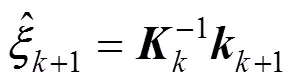
Substituting Eq. (27) into Eq. (26), we get the length of the residual,
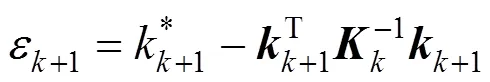


Then the recursion of+1can be computed by

Theorem 2 can be proven similarly to Theorem 1, which is omitted here.
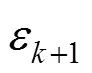
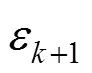
3.3 Procedure of the online algorithm
With above multi-output online algorithm, the procedure of online modeling a continuous process by LS-SVR can be designed as follows.
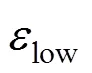

4 Online modeling of isomerization of C8 aromatics
4.1 Industrial flowsheet of isomerization unit
The PX joint process in a refinery comprises PX adsorption separation unit, xylene isomerization unit and xylene rectification unit. The PX adsorption separation unit is for separation of PX from other three isomers. In the xylene isomerization unit, the C8aromatics with lean PX from the adsorption separation unit is converted to C8aromatics with balanced PX under the influence of catalyst. The xylene rectification unit has two functions, to supply raw material C8aromatics to the adsorption separation unit and supply heat to other two units.
The industrial flowsheet of isomerization of C8aromatics is shown in Fig. 1. The C8aromatics with lean PX from the adsorption separation unit, together with C8-paraffin and polymethylene [C8(N+P)] fraction from recycle column T302 and recycle hydrogen from compressor, exchange heat with reaction product in heat exchanger E301. Then the mixture is heated to the required temperature in the furnace F301 and reacts in the reactor R301 to realize the equilibrium of the PX in C8aromatics. The reaction product is delivered into the gas-liquid separator V301 after condensation in condenser A301. The gas product from V301 is utilized as recycle hydrogen while the liquid product enters the heptane deprivation column T301. The top component of column T301, comprising light component below heptane and C8(N+P), enters the refluence tank Y302, some of which flows back to the top of the column, and the rest is delivered into recycle column T302 for separation of C8(N+P) component and returns to the isomerization reactor. The main bottom components of column T301 are C8aromatics, which is delivered into the rectification unit.

Figure 1 Industrial flow chart of isomerization of C8aromatics
1—reactor; 2—furnace; 3—heat exchanger; 4—condenser; 5—gas-liquid separator; 6—heptane deprivation column; 7,9—refluence tank; 8—recycle column
4.2 Simulation results
The percentage of PX in the feed of the heptane deprivation column, isomerization yield of PX and conversion of EB, from which the quality of isomerization process can be evaluated, are selected as the output variables of the model. According to the kinetic model and industrial experience, the main factors affecting the reaction are reaction temperature, pressure, the total feed and concentrations of PX, MX, OX, EB, and C8(N+P) in the feed, weight space velocity (WHSV), and ratio of H2to hydrocarbon (H2/HC). These 10 variables are selected as the inputs of the model, as listed in Table 1. The total feed of the reactor is composed of the fresh feed from the adsorption separation unit and the recycle feed from the recycle column. Accordingly, the components of the total feed are the weighted results of corresponding components of the fresh feed and the recycle feed.

Table 1 Input and output variables of the model
A total of 490 data samples were collected from a practical isomerization process of C8aromatics from June 1, 2004 to March 31, 2005. The sampling period is6 h. To illustrate the performance of online multi-output LS-SVR, we train the LS-SVR by standard LS-SVR, online LS-SVR and sparse online LS-SVR separately.
The radial basis function (RBF)

is chosen as the kernel function in the experiment.

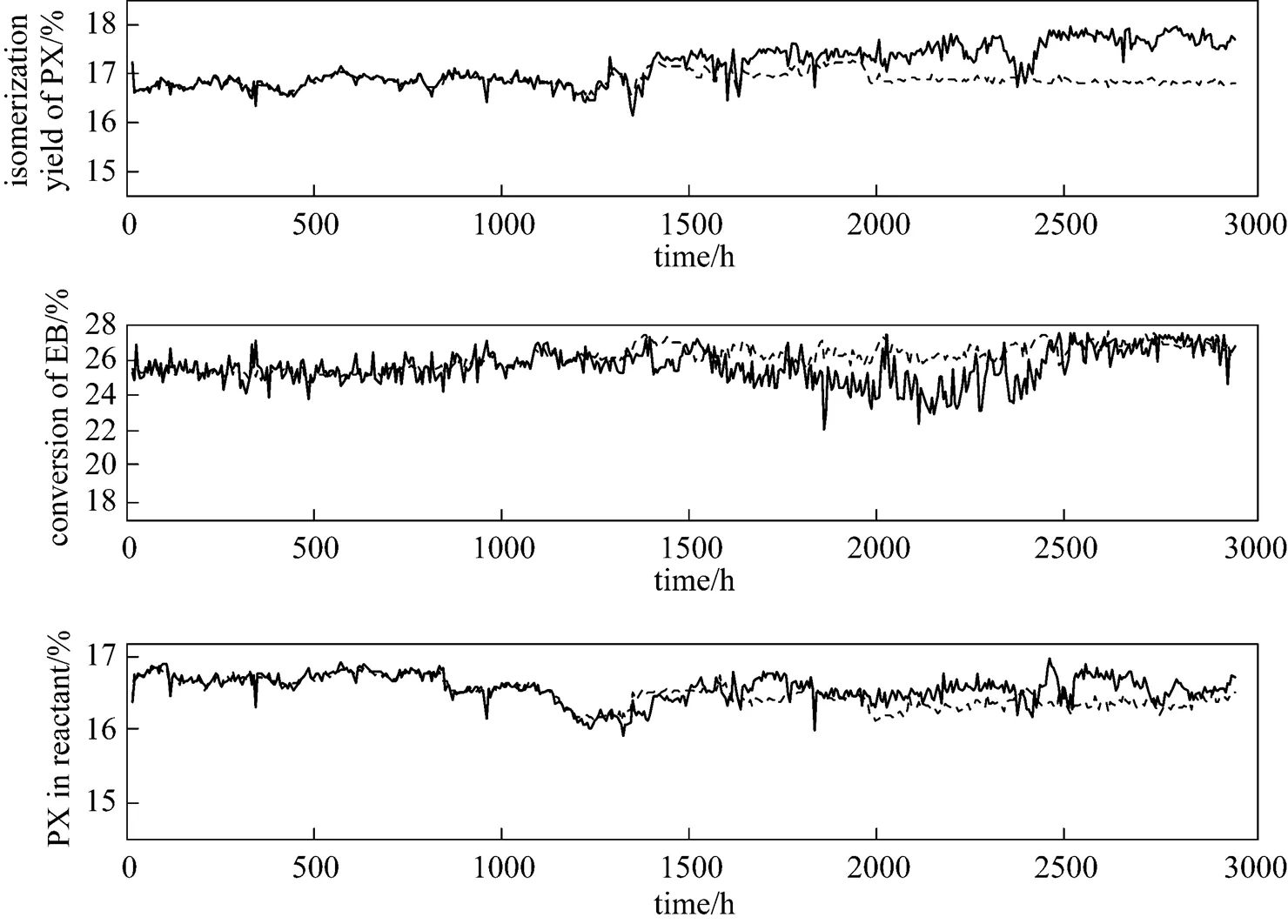
The predictive result of nonsparse online LS-SVR is shown in Fig. 3. The online LS-SVR is obviously superior to standard LS-SVR in the predictive precision as the operation condition changes.

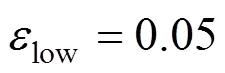
The root-mean-square-error (RMSE) is defined to evaluate the performance in our experiments,


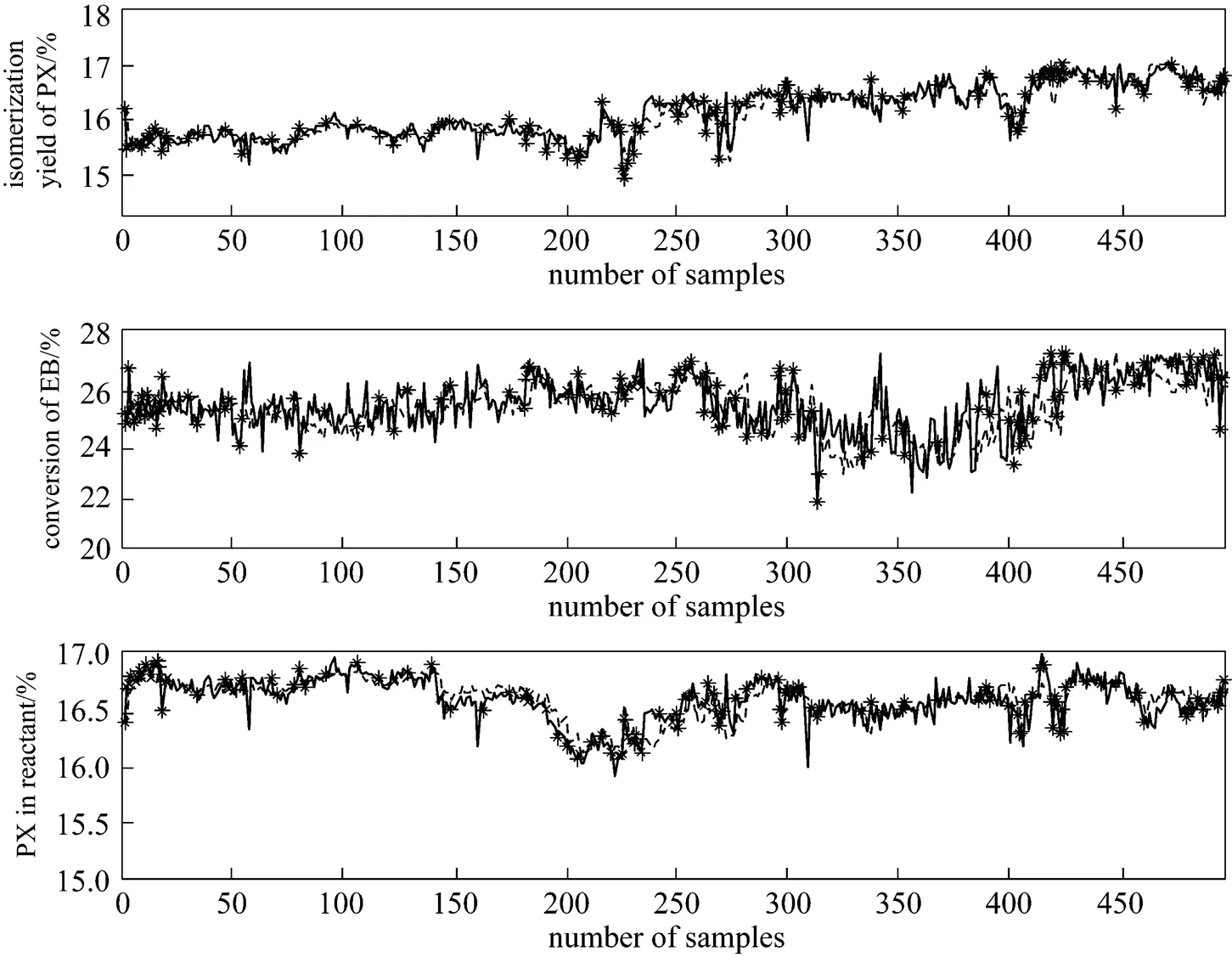

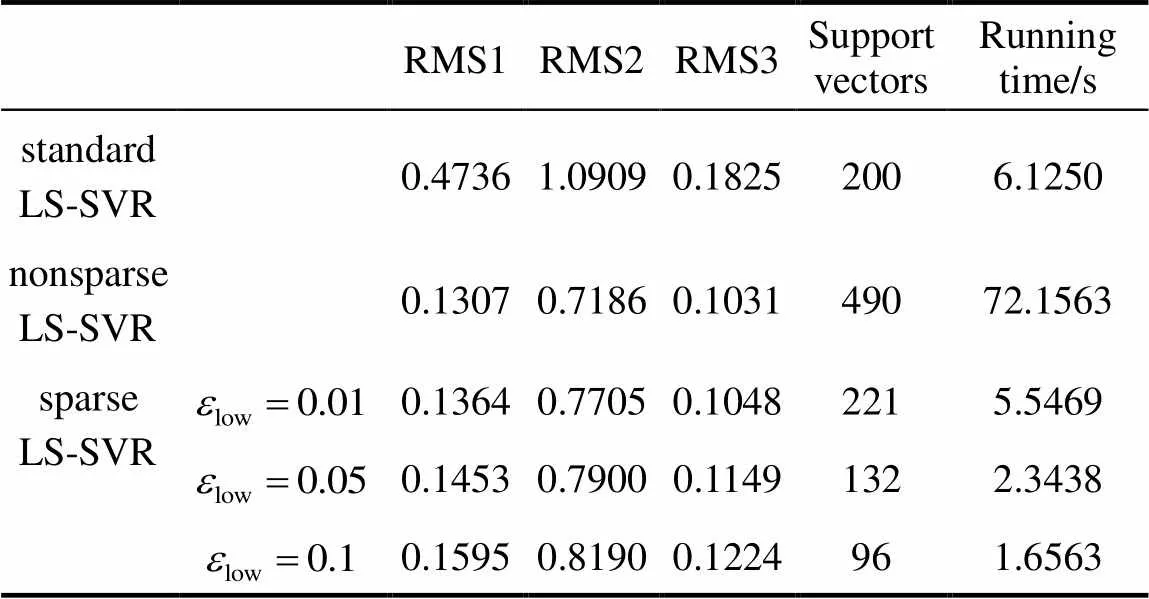
Table 2 Comparison of three LS-SVR algorithms
It can be seen from Table 2 that the accuracy of online LS-SVR is much higher than the standard LS-SVR, especially when the operation condition changes. Nonsparse online LS-SVR shows the highest precision but the longest running time. The sparse online LS-SVR solves the running time problem perfectly with a minor influence of the precision. Smallerlowgives higher precision and longer running time. Therefore, the trade-off between the precision and running time can be obtained by regulating the thresholdlow.
5 Conclusions
The proposed multi-output online sparse LS-SVR is a practical algorithm for online modeling of multi-variable industrial processes, which achieves relatively high precision with less computation. The inversion of large matrix is avoided and the computing time is decreased by passing over some samples based on projection method. At the same time, by online modifying the model, higher predictive accuracy is obtained. The example of isomerization of C8aromatics indicates the practicability of the presented method for actual processes.
1 Horacio, G., Abante, R., Luis, C., Jorge, R., “Isomerization of C8aromatics over a Pt/Mordenite Catalyst. A statistical model”,...., 35, 3964-3972 (1996).
2 Xu, O.G., Su, H.Y., Jin, X.M., Chu, J., “Kinetic model for hydroisomerization reaction of C8aromatics”,....., 21 (3), 429-435 (2007).
3 Li, Y.G., Chang, X.D., Zeng, Z.H., “Kinetics study of the isomerization of xylene on HZSM-5 zeolite.1.Kinetics model and reaction mechanism”,...., 31 (1), 187-192 (1992).
4 Iliyas, A., Al-Khattaf, S., “Xylene isomerization over USY zeolite in a riser simulator: A comprehensive kinetic model”,...., 43, 1349-1358 (2004).
5 Wu, D.X., Lin, Z.X., “Kinetic modeling of hydroisomerization of C8aromatics (I) Modeling and estimation of relative rate constants by the wei-prater method”,.... (), 3, 257-267 (1985). (in Chinese)
6 Wu, D.X., Lin, Z.X., “Kinetic modeling of hydroisomerization of C8aromatics (II) Mathematical expression of ray vector and its application”,.... (), 3, 268-277 (1985). (in Chinese)
7 Li, Z.H., Chen, D.Z., Zhuang, L., Hu, S.X., “RBF-MCSR approach as modeling technique for equipment of isomerization of xylene”,.... (), 6, 627-632 (2002). (in Chinese)
8 Yan, X., “Aromatic hydrocarbon isomerization process modeling based on adaptive artificial neural networks”,, 33 (5), 6-8(2006).
9 Vapnik, V., Statistical Learning Theory, John Wiley, New York (1998).
10 Vapnik, V., The Nature of statistical Learning Theory, Spring-Verlag, New York (1995).
11 Suykens, J. A.K., Vandewalle, J., “Least squares support vector machine classifiers”,, 9, 293-300 (1999).
12 Lee, D.E., Song, J.H., Song, S.O., Yoon, E.S., “Weighted support vector machine for quality estimation in the polymerization process”,...., 44 (7), 2101-2105 (2005).
13 Zhang, Y., Su, H.Y., Liu, R.L., Chu, J., “Fuzzy support vector regression model of 4- CBA concentration of industrial PTA oxidation process”,...., 13 (5), 642-648 (2005).
14 Zheng, X., Qian, F., “Application of least squares support vector machine within evidence framework in PTA process”,.... (), 57 (7), 1612-1616 (2006). (in Chinese)
15 Li, L., Su, H.Y., Chu, J., “Generalized predictive control with online least squares support vector machines”,, 33 (11), 1182-1188 (2007).
16 Suykens, J.A.K., Vandewalle, J., “Multiclass least squares support vector machines”, In: International Joint Conference on Neural Networks, Washington (1999).
17 Ljung, L., System Identification—Theory for the User, Prentice Hall PTR, Sebastopol (1999).
2008-04-30,
2009-03-20.
the National Creative Research Groups Science Foundation of China (60721062) and the National Basic Research Program of China (2007CB714000).
** To whom correspondence should be addressed. E-mail: ljli@njut.edu.cn
杂志排行
Chinese Journal of Chemical Engineering的其它文章
- Position Group Contribution Method for Estimation of Melting Point of Organic Compounds
- Process Intensification of VOC Removal from High Viscous Media by Rotating Packed Bed*
- Adsorption of Dye from Wastewater by Zeolites Synthesized from Fly Ash: Kinetic and Equilibrium Studies*
- Resolution of Ibuprofen Ester by Catalytic Antibodies in Water-miscible Organic-solvents*
- Reaction Characteristics of Asymmetric Synthesis of (2S,5S)-2,5-Hexanediol Catalyzed with Baker’s Yeast Number 6*
- Gross Error Detection and Identification Based on Parameter Estimation for Dynamic Systems*
