Cryogenic Liquid Slug and Taylor Bubble Length Distributions in an Inclined Tube*
2009-05-14WANGShuhua王淑华ZHANGHua张华andWANGJing王经
WANG Shuhua (王淑华)**, ZHANG Hua (张华) and WANG Jing (王经)
Cryogenic Liquid Slug and Taylor Bubble Length Distributions in an Inclined Tube*
WANG Shuhua (王淑华)**, ZHANG Hua (张华) and WANG Jing (王经)
Institute of Engineering Thermo-physics, Shanghai Jiao Tong University, Shanghai 200240, China
An experimental study was carried out to understand the phenomena of the boiling flow of liquid nitrogen in an inclined tube with closed bottom by using a high speed motion analyzer. The experimental tube is 0.018 m ID and 1.0 m in length. The range of the inclination angle is 45º-90º from the horizontal. The experiment focused on the effect of the inclination angle show that the mean liquid slug length and Taylor bubble length increase with the increasing/at various inclination angles. At the same/, the mean liquid slug length and Taylor bubble length increase first, and then decrease with decreasing inclination angles, with the maximum at 60º. In the vertical tube, standard deviation of the nitrogen Taylor bubble length increase with the increasing/. For the inclined tube, standard deviation of the nitrogen Taylor bubble length increases first, and then decreases with the increasing/. Standard deviation of the liquid slug length increases with increasing/for all inclination angles.
nitrogen, boiling, Taylor bubble, liquid slug, length distribution, inclined tube
1 INTRODUCTION
Gas-liquid slug flow is highly complex with an inherent unsteady behavior. It is characterized by long bullet-shaped bubbles separated by liquid slugs that may be aerated by small dispersed bubbles. Slug flow is found in many industrial applications, such as heat exchangers, nuclear reactor emergency core cooling, transport and handling of cryogenic fluids.
In the high-temperature devices cooling process by using cryogenic fluids, superheating always exists in the conveyor and storage system of cryogenic liquid. Then cryogenic two-phase flow is unavoidable. The propagation and storage of cryogenic liquids bring many problems, such as geysering, stratification and rollover [1]. Above phenomenon can cause high transient pressures and vapor flow rates, in some cases large enough to damage equipment. These bring challenges to the multi-phase flow theory in cryogenic engineering. The identification of flow patterns in vertical and inclined conveying tube is an important issue in many research fields of cryogenic two-phase flow. Many experimental and numerical papers [2-19] address the slug flow using air-water, oil or kerosene as working fluids. And most of those papers were on horizontal or slightly inclined slug flow and for vertical flow. The liquid slug and Taylor bubble lengths distribution can be described by positively skewed distributions,such as log-normal, gamma, or inverse Gaussian ones [8, 20].
Cryogenic vapor-liquid slug flow is seldom studied in inclined tube with closed bottom. Compared with normal atmospheric temperature liquid, cryogenic liquid has high compressibility, low density difference between vapor and liquid, and low latent heat of vaporization. There is great difference of bubble motion between cryogenic two-phase flow and normal temperature two-phase flow.
The purpose of the present study is to investigate experimentally the distribution of the liquid slug length and the nitrogen Taylor bubble length in inclined tube with closed bottom. The liquid nitrogen is used as working medium.
2 EXPERIMENTAL
In the experiment, the range of inclination angle is 45º-90º with respect to the horizon. The tube section of 20-50from the bottom of tube is measured by using high speed motion analyzer.
2.1 Experimental apparatus
Figure 1 shows the schematic diagram of the experimental apparatus. The main body of the setup, which is made of a jacketed Pyrex glass tube, includes a 1.0 m long test section with inner diameter 0.018 m, and an upper stock tank with inner diameter 0.1 m and 0.4 m length. The main body can be rotated around its axis and fixed at 40º-90º inclination angles from the horizontal. The vacuum jacket is 0.021 m thick and the attainable vacuum is 6×10-2Pa.
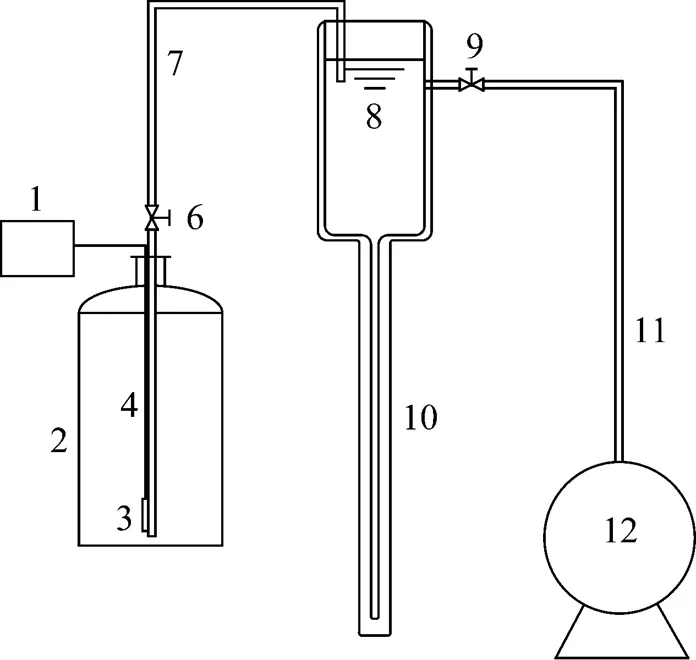
Figure 1 Experimental apparatus
1—power supply; 2—nitrogen Dewar; 3—electric heating rod; 4—power cord; 5—liquid nitrogen delivery tube; 6—ball valve; 7—flexible tube; 8—upper stock tank; 9—vacuum valve; 10—test section; 11—vacuum tube; 12—vacuum pump
The liquid nitrogen stored in a Dewar is supplied to the test section with the help of the high-pressure nitrogen gas in Dewar, which is generated by an electric heating rod. The liquid level of the upper stock tank is controlled between 1.16 m and 1.18 m to insure the tube full of liquid nitrogen. The heating is switched off when the liquid level in the upper tank is higher than 1.18 m, and is switched on when the liquid level falls to lower than 1.16 m. Vapor generation rate is 0.089×10-3kg·s-1by controlling the rate of heat leakage. Vapor bubble generation was observed throughout the test tube, and the superficial vapor velocity was 0.077 m·s-1at the end of the test section.
2.2 High speed motion analyzer
Figure 2 is the schematic of the image processing system. The high speed motion analyzer (Redlake Motion-Pro®X3, 1280×1024 pixels resolution, 1000 frames·s-1with the full resolution) was employed. In the experiment, the pixels resolution was 512×512, and the frame rate was 1000 frame·s-1. The recorded images were transmitted to the computer for further analysis. Two photoflood lamps with the total power of 1000 W were used as light source.
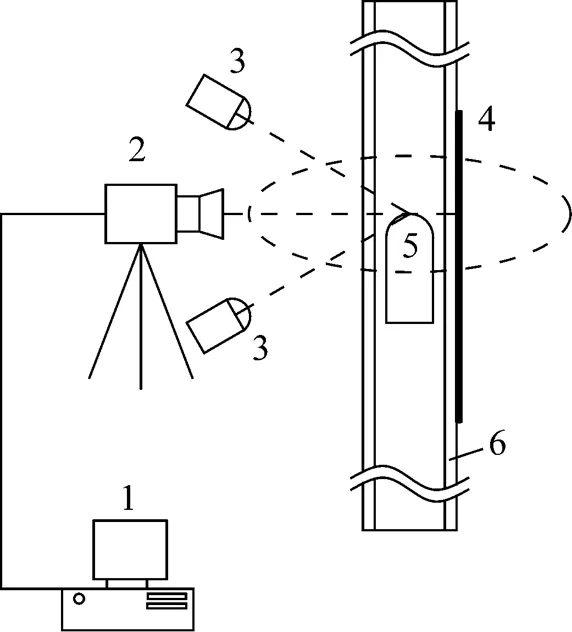
Figure 2 The schematic design of image processing system
1—computer; 2—high speed motion analyzer; 3—light; 4—screen; 5—Taylor bubble; 6—vacuum interlayer
2.3 Image processing
The local propagation bubble velocity of the bubble interface is calculated as the shift of the corresponding interface, divided by the time elapsed between the frames:
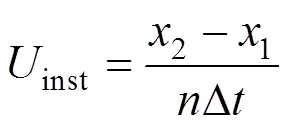
The Taylor bubble length is determined by multiplying the transit time of a vapor bubble over the measured distance by the bubble nose velocity. In the same way, the value of the liquid slug length is obtained.
3 RESULTS
3.1 Liquid slug and nitrogen Taylor bubble video images
Figures 4 and 5 show the evolution of the liquid slug and nitrogen Taylor bubble along the tube at various inclination angles. Fig. 4 indicates that the shape of the nitrogen Taylor bubbles shows great difference with the change of inclination angles along the tube, that is to say, the whole nitrogen Taylor bubbles are near the center of tube at 90º, 80º, 70º, as well as the tube upper wall at 60º and 45º. The left of the video images (Fig. 5) are the bottom of the leading nitrogen Taylor bubbles, and the right are the nose of the trailing nitrogen Taylor bubbles. Fig. 5 indicates that more and more small bubbles in liquid slug regions are near the tube upper wall with decreasing angles.
3.2 Liquid slug and nitrogen Taylor bubble lengths distribution
The histograms showing the distribution of liquid slug and nitrogen Taylor bubble lengths are given in Figs. 6 and 7. In general, the mean and the mode of the length distributions increase along the tube and both the liquid slug and the nitrogen Taylor bubble length distributions are left-skewed in all cases.
The effect of the inclination angle on the measured nitrogen Taylor bubble and liquid slug length distributions is shown in Figs. 6 and 7 at different locations along the tube. The mean and the most mode liquid slug lengths increased first, and then decreased with decreasingwhereis the inclination angle of the tube, maximum at 60º, and the distributions become more inhomogeneous with decreasing. Similarly, the mean and the most probable elongated bubble lengths exhibit a maximum at 60º.
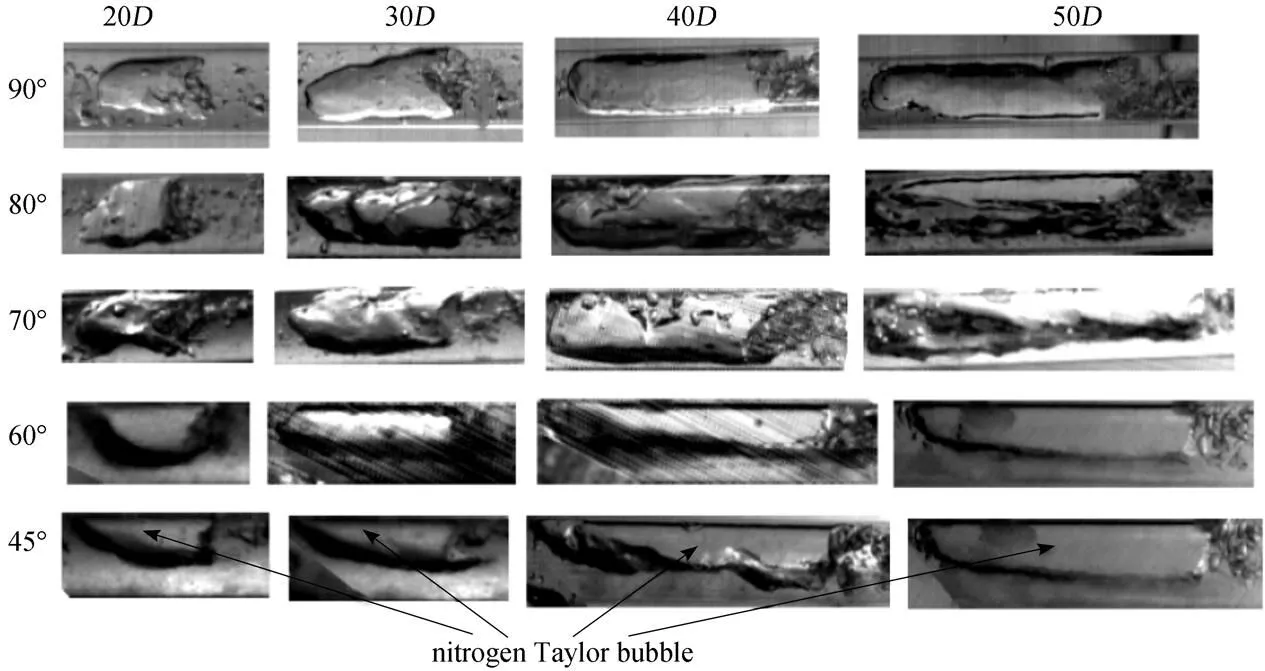
Figure 4 Nitrogen Taylor bubble images along the tube at various inclination angles
Figure 5 Liquid slug images along the tube at various inclination angles

Figure 6 Liquid slug length distribution along the tube at various inclination angles
3.3 Mean Taylor bubble and liquid slug lengths and standard deviation
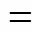
Figure 9 presents the evolution of the dimensionless liquid slug and nitrogen Taylor bubble lengths standard deviations as a function of inclination angle. In vertical tube, the nitrogen Taylor bubble lengths standard deviation increases with increasing/. For inclined tube, the nitrogen Taylor bubble lengths standard deviation increases first, and then decreases with increasing/which shows Taylor bubble length distribution is more homogeneous when/is greater than 40. Contrary to the nitrogen Taylor bubble length standard deviation, liquid slug length standard deviation increases with increasing/in all cases which shows the liquid slug length distribution is inhomogeneous with increasing/.
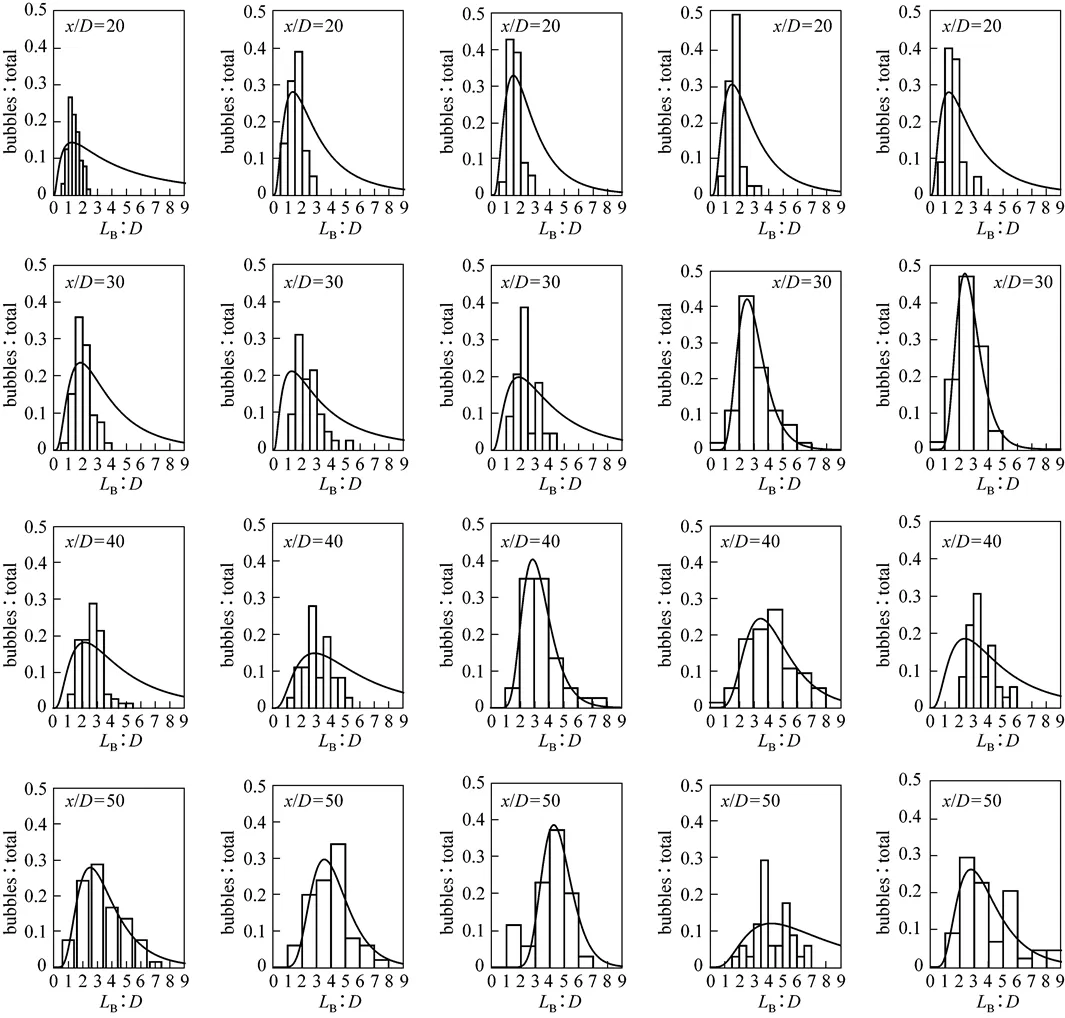
Figure 7 Nitrogen Taylor bubble length distribution along the tube at various inclination angles
3.4 The log-normal distributions of liquid slug and nitrogen Taylor bubble lengths
Figures 6 and 7 show both the liquid slug and the nitrogen Taylor bubble length distributions are left-skewed in all cases. The log-normal shape is fitted to the measured distributions and is depicted in Figs. 6 and 7 as a solid line. The probability density function of the log-normal [21] distribution is
4 CONCLUSIONS
An experimental study on the evolution of continuous liquid nitrogen boiling flow along inclined tube with inner diameter 0.018 m is presented. The liquid slug and nitrogen Taylor bubble length distributions are investigated. The measurement was carried out by high speed motion analyzer along the tube at various inclined angles.
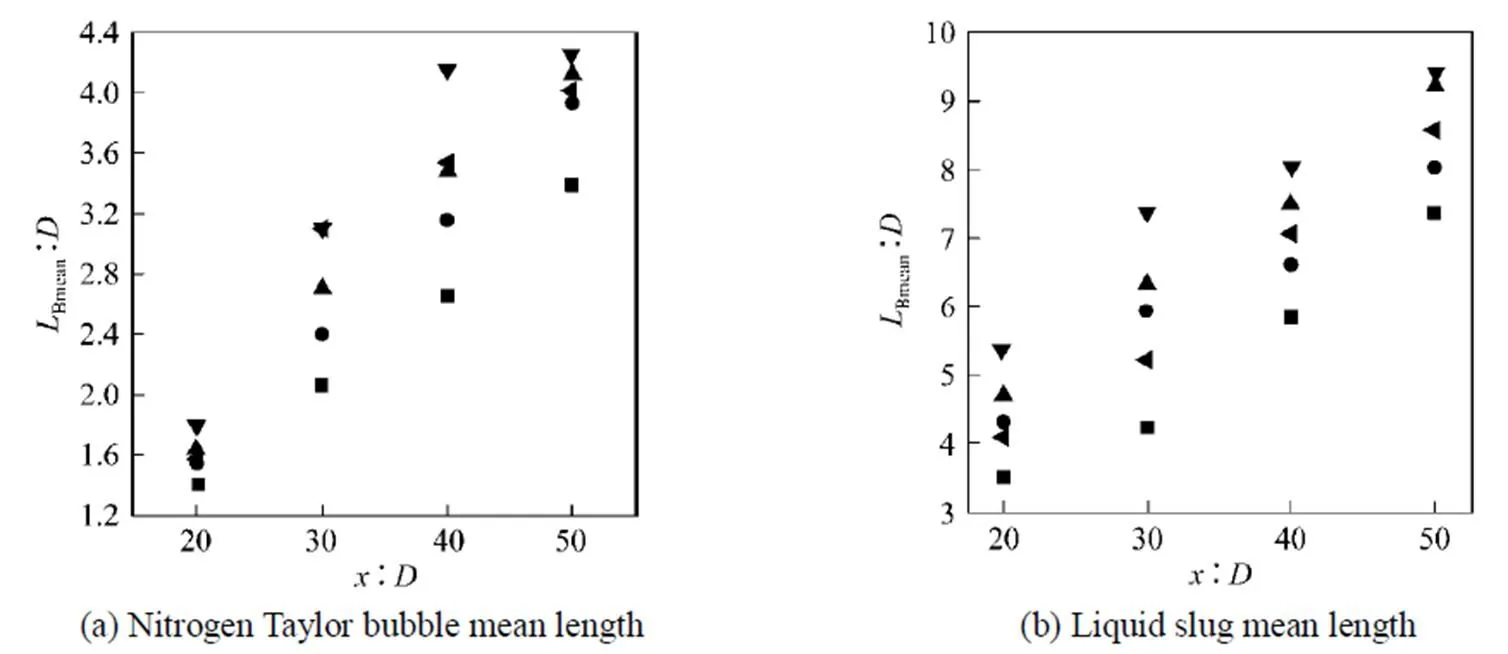
Figure 8 Nitrogen Taylor bubble mean length and liquid slug mean length along the tube at various inclination angles
■ 90o; ● 80o; ▲ 70o; ▼ 60o; ◄ 45o
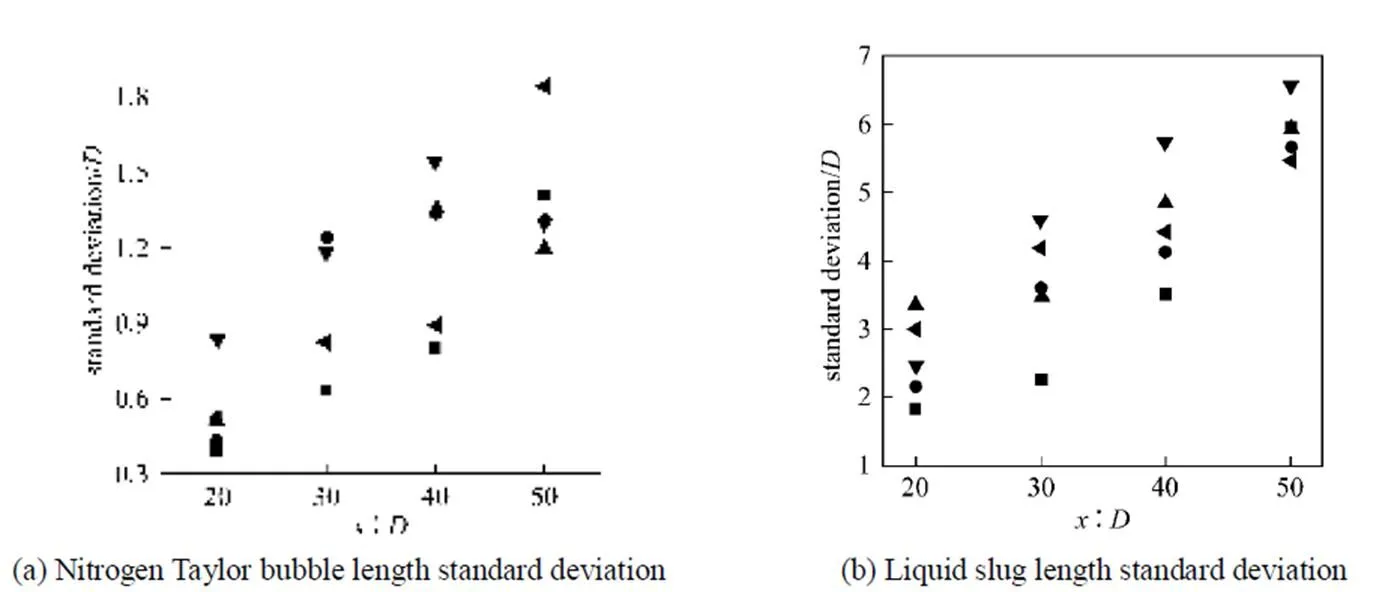
Figure 9 Nitrogen Taylor bubble length and liquid slug length standard deviations along the tube at various inclination angles
■ 90o; ● 80o; ▲ 70o; ▼ 60o; ◄ 45o
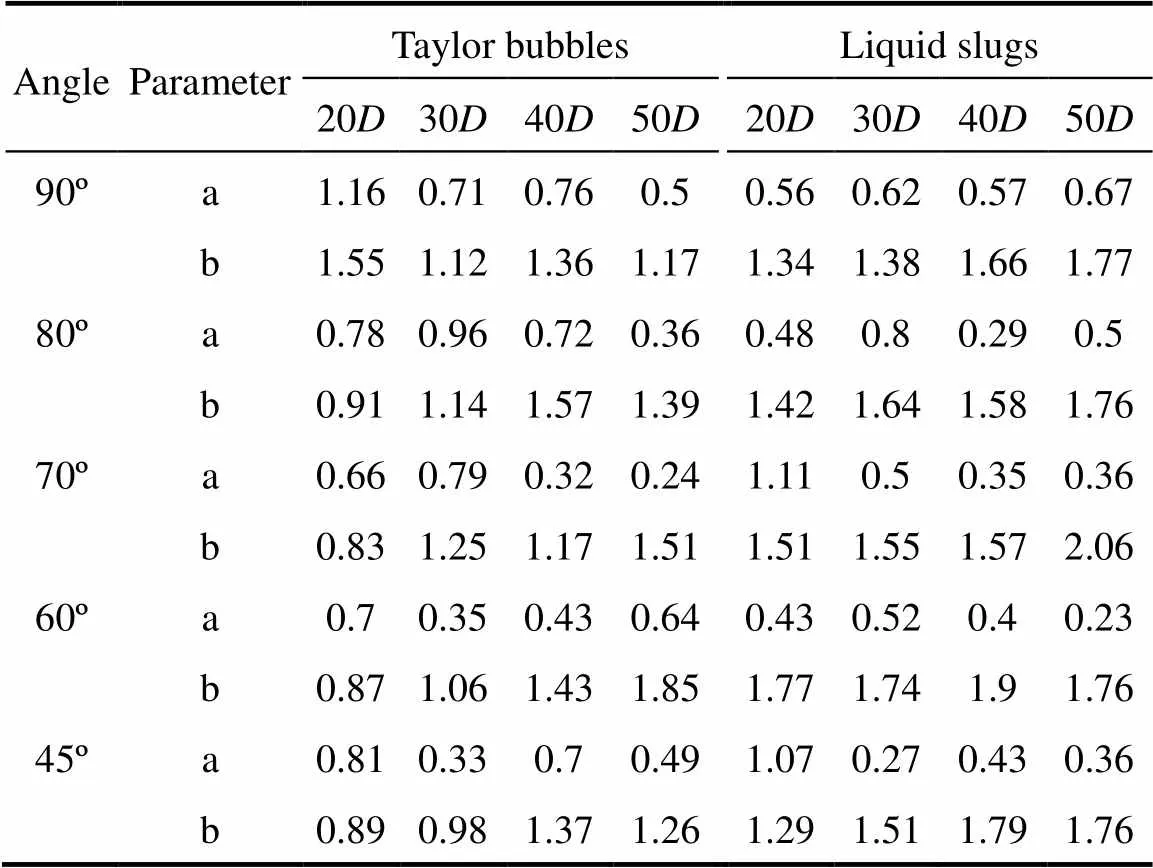
Table 1 Parameters a and b of log-normal fit
Through images analyzing, the whole nitrogen Taylor bubble was near the center of tube at 90º, 80º, 70º, but at the tube upper wall at 60º and 45º. More and more small bubbles in the liquid slugs were near the tube upper with decreasing angles.
For all cases, measured length distributions were well described by the log-normal function. The mean liquid slug lengths increased first, and then decreased with decreasing, but the maximum was at 60º. This result showed Taylor bubble was easier to coalescence in inclined tube than in vertical flow, but coalescence was the least at 45º. Similarly toSmean,Bmeandepended on the tube inclination as well, and the longest bubbles are observed at 60º.
For an inclined tube, the nitrogen Taylor bubble lengths standard deviation increased first and then decreased with increasing/, which showed the Taylor bubble length distribution was more homogeneous when/was greater than 40. Contrary to nitrogen Taylor bubble length standard deviation, liquid slug length standard deviation increased with increasing/in all cases, suggesting the liquid slug length distribution became inhomogeneous with increasing/.
1 Hands, B.A., “Problems due to superheating of cryogenic liquids”,, 28 (12), 823-829 (1988).
2 Gu, H.Y., Guo, L.J., “Experimental investigation of slug development on horizontal two-phase flow”,...., 16 (2), 171-177 (2008).
3 Wang, X., Guo, L.J., Zhang, X.M., “Development of liquid slug length in gas-liquid slug flow along horizontal pipeline: experiment and simulation”,...., 14 (5), 626-633 (2006).
4 Dukler, A.E., Hubbard, M.G., “A model for gas-liquid slug flow in horizontal and near horizontal tubes”,...., 14 (4), 337-347 (1975).
5 Nicholson, M.K., Aziz, K., Gregory, G.A., “Intermittent two-phase flow in horizontal pipes: predictive models”,...., 56 (12), 653-663 (1978).
6 Andreussi, P., Bendiksen, K., “An investigation of void fraction in liquid slugs for horizontal and inclined gas-liquid pipe flow”,.., 15 (6), 937-946 (1989).
7 Nydal, O.J., Pintus, S., Andreussi, P., “Statistical characterization of slug flow in horizontal pipes”,.., 18 (3), 439-453 (1992).
8 Cook, M., Behnia, M., “Slug length prediction in near horizontal gas–liquid intermittent flow”,..., 55 (11), 2009-2018 (2000).
9 He, L.M., “An investigation of the characteristics of oil-gas two-phase slug flow in horizontal pipes”, Ph. D.Thesis, Xi’an Jiaotong Univ., China (2002).
10 Barnea, D.A., Taitel, Y., “A model for slug length distribution in gas-liquid slug flow”,.., 19 (5), 829-838 (1993).
11 Mao, Z.S., Dukler, A.E., “Improved hydrodynamic model of two-phaseslug flow in vertical tubes”,...., 1 (1), 18-29 (1993).
12 Xia, G.D., Zhou, F.D., Hu, M.S., “An investigation on the void fraction for upward gas-liquid slug flow in vertical pipe”,...., 9 (4), 436-440 (2001).
13 Mao, Z.S., Dukler, A.E., “An experimental study of gas-liquid slug flow”,., 8 (2), 169-182 (1989).
14 Xia, G.D., Liu, L., Ma, C.F., Yuan, Z.X., Zhou, F.D., Hu, M.S., “An experimental study on gas liquid two-phase slug flow-liquid slug length and the fraction of Taylor”,...., 26 (2), 35-38 (1997). (in Chinese)
15 Costigan, G., Whalley, P.B., “Slug flow regime identification from dynamic void fraction measurements in vertical air-water flows”,nt.., 23 (2), 263-282 (1997).
16 van Hout, R., Barnea, D., Shemer, L., “Evolution of statistical parameters of gas-liquid slug flow along vertical pipes”,.., 27 (9), 1579-1602 (2001).
17 Felizola, H., Shoham, O., “A unified model for slug flow in upward inclined pipes”,..., 117 (1), 7-12 (1995).
18 van Hout, R., Shemer, L., Barnea, D., “Evolution of hydrodynamic and statistical parameters of gas-liquid slug flow along inclined pipes”,..., 58 (1), 115-133 (2003).
19 van Hout, R., Shemer, L., Barnea, D., “Spatial distribution of void fraction within the liquid slug and some other related slug parameters”,.., 18 (6), 831-845 (1992).
20 Brill, J.P., Schmidt, Z., Coberly, W.A., Herring, J.D., Moore, D.W., “Analysis of two-phase tests in large-diameter flow lines in Prudhoe Bay Field”,...., 271 (6), 363-378 (1981).
21 Jin, G.Y., Wang, F.X., Wang, S.C., Engineering Data Statistics Analysis, Southeast University Press, Nanjing (2002). (in Chinese)
2008-06-12,
2008-09-22.
the National Natural Science Foundation of China (50476015) and National High Technology Research and Development Program of China (2006AA09Z333).
** To whom correspondence should be addressed. E-mail: shhwang@sjtu.edu.cn
杂志排行
Chinese Journal of Chemical Engineering的其它文章
- Modeling and Optimization for Scheduling of Chemical Batch Processes*
- Simulation of Droplet-gas Flow in the Effervescent Atomization Spray with an Impinging Plate*
- Numerical Investigation of Constructal Distributors with Different Configurations*
- The Kinetics of the Esterification of Free Fatty Acids in Waste Cooking Oil Using Fe2(SO4)3/C Catalyst
- Multiple Model Soft Sensor Based on Affinity Propagation, Gaussian Process and Bayesian Committee Machine*
- Measurement and Correlation of Solid-Liquid Equilibria of Phenyl Salicylate with C4 Alcohols
