Modeling and Optimization for Scheduling of Chemical Batch Processes*

QIAN Yu (钱宇)**, PAN Ming (潘明) and HUANG Yacai (黄亚才)



Modeling and Optimization for Scheduling of Chemical Batch Processes*

QIAN Yu (钱宇)**, PAN Ming (潘明) and HUANG Yacai (黄亚才)

School of Chemical Engineering, South China University of Technology, Guangzhou 510640, China

Chemical batch processes have become significant in chemical manufacturing. In these processes, large numbers of chemical products are produced to satisfy human demands in daily life. Recently, economy globalization has resulted in growing worldwide competitions in traditional chemical process industry. In order to keep competitive in the global marketplace, each company must optimize its production management and set up a reactive system for market fluctuation. Scheduling is the core of production management in chemical processes. The goal of this paper is to review the recent developments in this challenging area. Classifications of batch scheduling problems and optimization methods are introduced. A comparison of six typical models is shown in a general benchmark example from the literature. Finally, challenges and applications in future research are discussed.

chemical batch processes, scheduling, optimization methods

1 INTRODUCTION

Nowadays, batch processes play an important role in chemical processing industry. In batch processes, large numbers of chemical products are produced to satisfy human demand in daily life. Scheduling is crucial for improving the productivity of batch process. It is a decision making process to determine the locations, times and sequences for processing activities with finite units and resources to achieve certain objective, such as maximization of profit or minimization of makespan and impact on environment.

There are several excellent papers of reviews and comparative studies on scheduling of chemical processes. Floudas and Lin [1] compared discrete and continuous-time approaches for scheduling of multiproduct/multipurpose batch and continuous processes. They examined slot-based and precedence-based models in sequential process scheduling, and compared various event-based models in network process scheduling. Shaik. [2] compared slot-based, global event-based and unit-specific event-based formulations in network process scheduling under unlimited intermediate storage. The considered issues included problem size (the number of binary variable, continuous variables, and constraints), CPU times, and number of nodes needed to reach zero integrality gap. Mendez. [3] classified batch processes into sequential and network processes, and compared the effectiveness and efficiency of discrete and continuous-time models. In above reviews, however, no precedence- based model was addressed for multipurpose batch scheduling, and the scheduling problems can only be solved selectively with slot-based, global event-based or unit-specific event-based models.

In this paper, the recent developments in batch scheduling are revisited, and six typical models are compared in solving a general benchmark example from the literature. The compared models include: global event-based models (M&G model [4], CBM model [5]), unit-specific event-based models (I&F model [6], G&G model [7]), slot-based model (S&K model [8]), and the recent precedence-based model (PQL model [9]). Finally, challenges and applications in future research are discussed.

2 CLASSIFICATION OF BATCH SCHEDULING PROBLEMS

Based on the complexity and features of batch processing, all the batch processes are classified into two categories: sequential processes and network processes, as shown in Fig. 1.

Sequential processes consisting of sequential, single or multiple stages and units can be divided into two groups: multiproduct and multipurpose batch plants. In multiproduct batch plant, all batches are processed in the same production paths, and the processing sequences of batches in each unit are identical. While in multipurpose batch plant, the production paths of some batches may be in the opposite direction, and the kind of products processed in each unit may also be different from others. Because of the complex characteristics of multipurpose batch plants, the scheduling for multipurpose plants are significantly different from and more difficult than that for multiproduct plants [10, 11].

Distinct to sequential processes, network processes include more complex features where arbitrary operationaltopology can be handled. As network processes are a mix of convergent and divergent-flow-paths, material balances are required to be taken into account explicitly. Kondili. [12] proposed State-Task Network (STN) for presenting the topology of network processes, as presented in Fig. 1 (b). There are two types of nodes in the STN: the task nodes and the state nodes. The task nodes are rectangle and represent processing tasks. While the state nodes (symboled by circle) represent the raw material, intermediates, or final products. The fraction of a state transferred to or from a task, if not equal to one, is given beside the arc which links the corresponding state and task nodes. The direction of arc represents the task precedence. Pantelides extended the STN to the Resource-Task Network (RTN) [13], where processing equipment, storage, material transfer and utilities are described as resources in a unified way. In this paper, all network processes are shown with the STN representation.

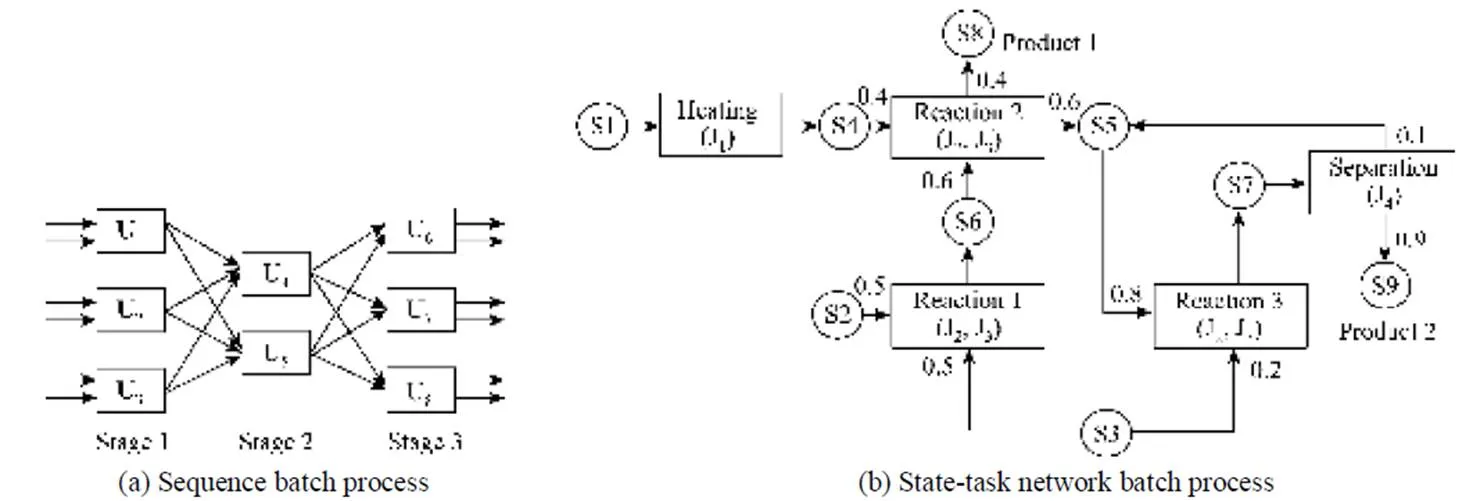
Figure 1 Batch processes

3 CLASSIFICATION OF OPTIMIZATION ME- THODS

Based on time representation, all existing formulations can be classified into two categories: discrete- time representations and continuous-time representations. In discrete-time approaches, a great deal of uniform time intervals are obtained by decomposing the time horizon and each task is executed during one or more intervals. While in continuous-time approaches, tasks can start and finish at any point in the continuous domain of time, so the time intervals are not uniform.

3.1 Discrete-time methods

Most of earlier works are based on discrete-time approaches. Kondili. [12] formulated the short-term scheduling problem as a mixed integer linear program (MILP) based on a discrete time representation. They considered flexible equipment allocation, variable batch sizes and mixed intermediate storage policies involving both dedicated and multipurpose storage vessels. Shah. [14] described a variety of techniques that exploit the characteristics of the problem in order to reduce the amount of computation required. However, discrete-time approaches usually need to divide time horizon into a huge number of small time intervals, leading to very large combinatorial problems, especially for scheduling of network processes, and thus limits their application.

3.2 Continuous-time methods

Due to the limitations of discrete-time approaches, continuous-time approaches are proposed for batch scheduling. These approaches are classified into four categories: precedence-based, slot-based, global-event based, and unit-specific-event based models.

3.2.1

In precedence-based models, batch allocation and sequencing decisions are modeled through sequencing binary variables, which directly represent the timing of the batches without the use of time slots. Cerda. [15] presented a new MILP mathematical formulation for the batch scheduling problem involving a single processing stage for every product to be delivered. Based on the concept of job predecessor and successor, real world single-stage scheduling problems can be handled efficiently. Mendez and Cerda [16] proposed MILP approach based on a continuous time domain representation and accounted for sequence-dependent setups. They handled the assignment and sequencing decisions independently through separate sets of binary variables, and reduced the number of sequencing variables and constrains with a proper formulation of the sequencing constraints. Recently, Pan. [9] proposed a novel precedence-based and heuristic approach for short-term scheduling of network processes. In their approach, binary variables expressed the assignments and sequences of batch processing and storing, an iterative procedure was developed to eliminate the drawback of precedence-based formulations, and four heuristic rules were proposed to reduce the overall number of binary variables. They found that the new model with these heuristic rules was more effective to find better solution for complex problems.

3.2.2

In slot-based models, the time horizon is divided into several unequal time intervals, and the tasks have to start and finish at an event. Pinto and Grossmann [17] proposed a slot-based model for the short term scheduling of multi-stage multi-product batch plants. To consider large scheduling problems, they used two solution strategies. The preordering constraints were used in the first strategy. While in the second strategy, a decomposition scheme for large systems was proposed with the solution of an MILP model. Lamba and Karimi [18] presented approaches based on the time slots defined for each unit to formulate continuous- time models for the scheduling of sequential multistage batch processes. Sundaramoorthy and Karimi [8] proposed a simpler slot-based model for short-term scheduling in multipurpose batch plants, and presented a novel idea of several balances. They claimed that their model used no big-M constraints, and was more effective than other proposed models for short-term scheduling of multipurpose batch plants.

3.2.3

Global-event-based models enforce that a set of events are common across all units and each task must either start or end (or both) at an event. Distinct to discrete-time approaches, Mockus and Reklaitis [19] used time directly to model events arising in the schedule. They formulated the scheduling problem as a mixed integer nonlinear program (MINLP) and simplified the resulting modelexact linearization to yield a mixed integer bilinear program (MIBLP) where the only nonlinearity arises in the objective function as a product of continuous variables. Maravelias and Grossmann [4] proposed a global event-based model for short-term scheduling of multipurpose batch plants relied on the state-task network (STN) approach. They defined binary variables only for tasks in assignment constraints, considered the finish time of tasks in time-matching constraints, and proposed a new class of valid inequalities to improve the LP relaxation of the MILP formulation. Pan. [10] used a decomposition approach to formulate the scheduling problem of sequential multipurpose batch plants. They replaced tri-index binary variables with bi-index binary variables, thus the number of binary variables decreased significantly.

3.2.4

Unit-specific-event-based models allow each task in a unit to start at an event, therefore each event can occur differently across different units. Ierapetritou and Floudas [6] decoupled the task events from the unit events, and used some time sequencing constraints in a mixed integer linear programming (MILP) model. The novel elements of the proposed formulation were (i) the decoupling of the task events from the unit events, (ii) the time sequencing constraints, and (iii) its linearity. Giannelos and Georgiadis [7]proposed an STN represented, unit-specific event-based formulation for short-term scheduling of multipurpose batch plants. In their model, event times are defined by the ends of task execution, and they are generally different for different tasks of the process, giving rise to a non-uniform time grid. Shaik. [2] slightly modified the model of Ierapetritou and Floudas (I&F), and compared this model with the corresponding slot-based and global-event models based on several benchmark example problems. They showed that although big-M constraints were used, the I&F model required fewer event points, thus performing the best in term of both computational performance and problem size.

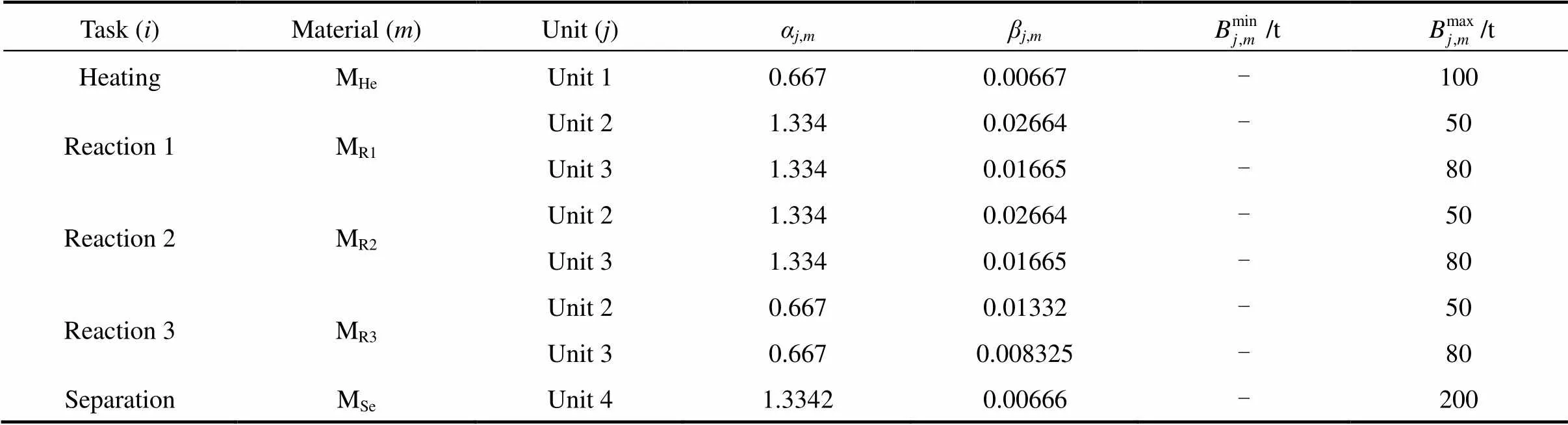
Table 1 Coefficients of processing times for tasks and limits on batch sizes of units

Table 2 Storage capacities, initial inventories, and revenues of materials

4 COMPARISON OF OPTIMIZATION MODELS

In the comparison studies, two intermediate storage policies (limited and unlimited intermediate storage) and two objective functions (maximization of profit and minimization of makespan) are considered. The compared items include problem size, computational times and model convergence. All the models are solved on the computer (2.16 GHz, Core 2 CPU with 1GB RAM) with running CPLEX 7.5.0 in GAMS 20.2. The computational results present the efficiency and limitations of the six models.

4.1 Maximization of profit

Model comparisons discussed below are under the maximization of profit. The model statistics and computational results are summarized in Table 3.

Two scenarios are considered for this example. In the first scenario (example 1a), time horizon () is 8 h. Since the time horizon is short, all the six models perform very well, as shown in Table 3. The PQL model gives the tightest relax objective, and requires fewer binary and continuous variables. The M&G model requires the most continuous variables and constraints, while the CBM model requires the most binary variables. In the second scenario (example 1b), time horizon () increases to 12 h. Three models, G&G, S&K and CBM models only find the suboptimal solutions. The M&G model takes a significantly long CPU time to get the optimal solution, while the I&F and PQL models requires very short times. Moreover, the PQL model requires fewest binary variables, and performs best among all models under limited and unlimited intermediate storage with respect to the model statistics.

4.2 Minimization of makespan

Minimization of makespan is the most difficult problem to solve, which had been considered in many research papers. The data of all benchmark example are the same as those shown in Tables 1 and 2, except that the time horizon () is varied and demands are fixed. Table 4 presents the model statistics and computational results under minimization of makespan.

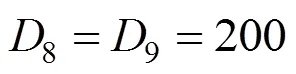
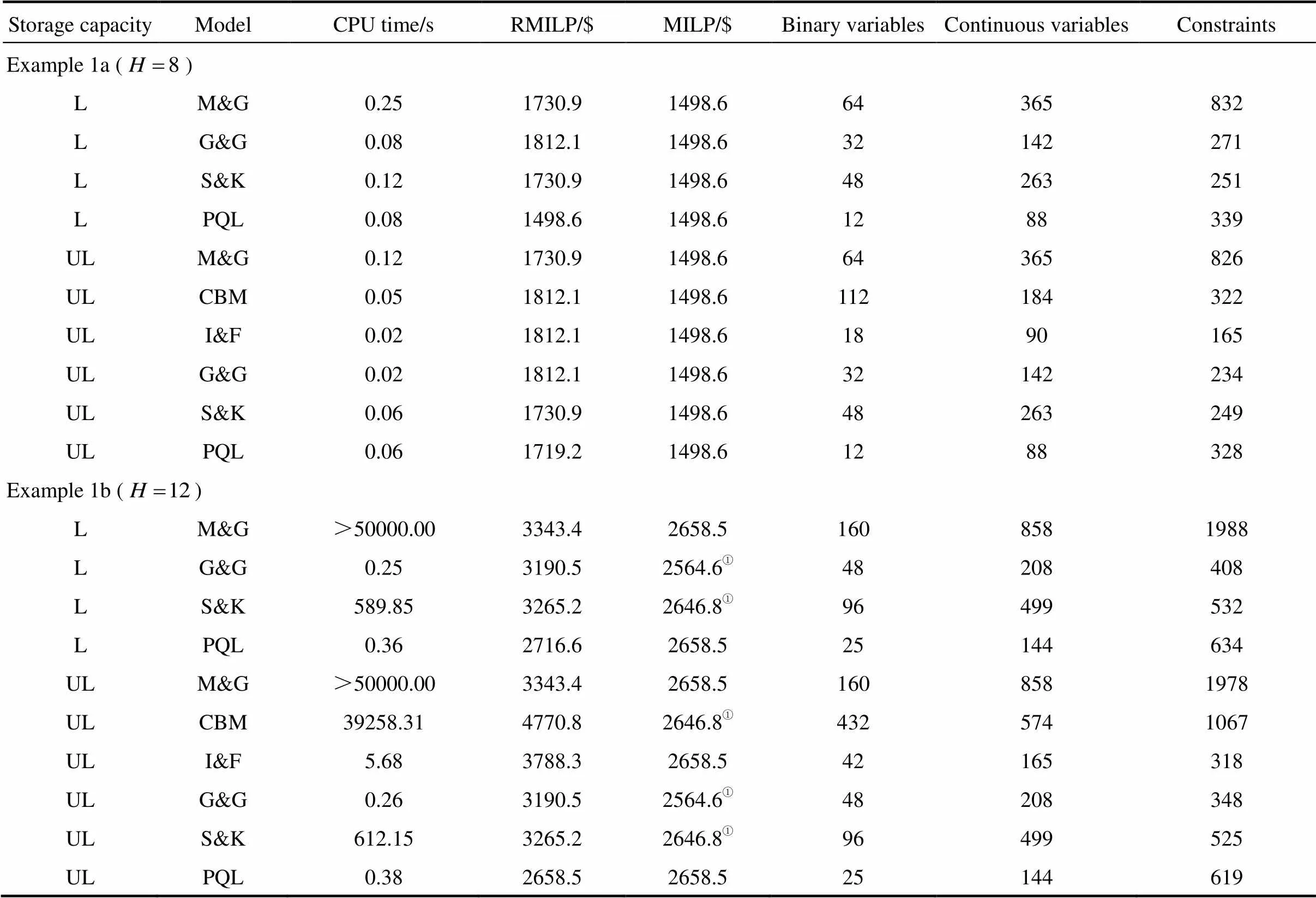
Table 3 Model statistics and computational results for benchmark example under maximization of profit

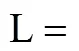
Table 4 Model statistics and computational results for example 2 under minimization of makespan

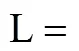
In simple scheduling problems, all models perform equally well. When time horizon becomes longer, only the PQL and I&F models require fewer binary variables, continuous variables and constraints, and find the optimal solutions in very short computational times. The M&G, S&K and CBM usually require lots of binary variables, continuous variables and constraints. These models only find the suboptimal solutions even though very long computational times are taken. Furthermore, the G&G model always gives the suboptimal solutions with using special sequencing constraints. Although the PQL model usually requires the same order of binary variables as the I&F model in most scheduling problems, the PQL model can solve scheduling problems efficiently both in limited and unlimited intermediate storage policies.

5 CHALLENGES AND RESEARCH PERSPECTIVES

Despite very significant progress has been made in short-term scheduling of network batch processes, a number of major challenges and questions must be taken into account. More specifically, future research efforts should aim at addressing following issues.

5.1 The modeling challenge

The area of scheduling has seen the development of many models in operation research (OR). The number of variables is crucial to scheduling models. Complex problems usually require lots of variables, continuous or discrete, for formulating. Normally, discrete variables affect the efficiency of MILP formulations, so they are called the key variables. To solve large scale scheduling problems, the number of key variables has to be decreased. But in combinatorial optimization models, the number of key variables will increase significantly with production period prolonging. For this reason, moderate-size problems requiring large numbers of binary variables are hard to be solved to optimality. Practically, the production experience of batch plant personnel can be used to determine the processing sequence of some batches, namely heuristic rules [9]. Some discrete variables can be prefixed selectively with these rules, and as a result, the feasible region of the problem decreases, which in turn increases the chance of finding better solutions within a finite period of computational time. Major issues here are the development of novel mathematical programming and logic-based models that can be effectively integrated to capture the complexity of the various operations. The novel mathematical programming can be developed with improving typical continuous-time methods, such as precedence-based, slot-based, global-event based, and unit-specific-event based models. While logic-based models, including heuristic rules or constraint programming, usually reduce the number of variables in mathematical programming modelsutilizing logical constraints from practical operations.

5.2 Medium-term scheduling

Medium-term scheduling of batch processes, which includes medium time horizon (.., several weeks) and needs to determine detailed production schedules, can lead to very large scale problems. To solve such computationally complex problem, which is computationally expensive or even intractable when formulated and solved directly as a single MILP model, some new mathematical programming techniques must be developed. The most widely employed strategy to overcome the computational difficulty is based on the idea of decomposition. The decomposition approach divides a medium-term problem into several smaller sub-problems. There have been a wide variety of decomposition approaches proposed in the literature. Although they substantially reduce the problem complexity and the solution time, most of them only lead to suboptimal solutions. A recent efficient approach can be referenced to eliminated the aforementioned drawback, where a decomposition model is implemented to determine each short horizon and the corresponding products to be included, and then, a novel continuous-time formulation for short-term scheduling of batch processes with multiple intermediate due dates is applied to each short horizon. The decomposition model and the short-term scheduling model are solved iteratively for each short horizon until the schedules for the whole period under consideration are generated. Major issues here include valid decomposition approaches and effective short-term scheduling models.

5.3 The uncertainty challenge

Most of the scheduling models for chemical processes assume that all problem parameters are constant known, namely deterministic models. However, uncertainty is prevalent in the context of scheduling in reality. A schedule generated by a deterministic model based on constant parameters may be infeasible upon real problems. Thus, uncertainty must be taken into account during the course of scheduling in order to improve the schedule quality. Stochastic scheduling is proposed to address the uncertainty information at the original scheduling stage. Its objective is to create optimal and reliable schedules in the presence of uncertainty. The consideration of uncertainty transforms the problem from a deterministic one to a stochastic problem, so special techniques are required. In stochastic programs, discrete probability distributions or the discretization of continuous probability distribution functions are used to described uncertain scenarios. The expectation of a certain performance criterion, such as the expected makespan, is optimized with respect to the scheduling decision variables. To solve a stochastic program, mathematical program is divided into a number of stages. Between each stage, some uncertainty is resolved, and the decision maker must choose an action that optimizes the current objective plus the expectation of the future objectives. Such methods provide a straightforward way to implicitly incorporate uncertainty. However, they inevitably enlarge the size of the problem significantly as the number of scenarios increases exponentially with the number of uncertain parameters. Major issues here are the development of novel, meaningful and effective stochastic programming tools.

5.4 The integration of scheduling with design and planning

The inherent operational flexibility of batch processes gives rise to the integration in the design, planning and scheduling. Normally, design, planning and scheduling are considered individually. In these cases, the resultant plan and schedule can not be integrated very well, which may lead to over-design or under-design. In order to use plant resources efficiently, detailed considerations of planning and scheduling must be taken into account at the design stage. Both planning and scheduling deal with the allocation of available resources over time to perform a set of tasks to manufacture one or more products. However, long-term planning problems deal with longer time horizons (.., several months or years) and make higher-level decisions such as the timing and location of additional facilities, and production demands. In contrast, short-term scheduling models address shorter time horizons (.., several days) and determine detailed sequencing of various operational tasks. To solve such multi-scale optimization problems, two major approaches can be utilized. (i) Common time grid: planning and scheduling are considered in the same time grid level, where the scheduling model is elevated to the planning level. The long time horizon is decomposed with time discretization, leading to a very large-scale multi-period problem. (ii) Decomposition techniques: planning and scheduling are integrated based on a two-level decomposition procedure, where the upper level problem (planning problem) is an aggregation of the lower level problem (scheduling). The challenge of developing an aggregated planning model is to yield tight bounds to reduce the number of upper and lower level problems. Major issues here involve novel decomposition procedures that can effectively work across large spatial and temporal scales.

6 CONCLUSIONS

This paper presents an overview of optimization methods for batch scheduling. The existing approaches are categorized into four classes: global event-based, unit-specific event-based, slot-based, and precedence-based models, respectively. A benchmark example is solved with different models. The model statistics and computational results show the strengths and limitations of six different methods. It is observed that reduction of large number of binary variables is an efficient way to solve the scheduling problems of batch processes. The major challenges and applications in future research are discussed. Despite very significant progress has been made in batch scheduling problems, the dynamic and systematic solution of integrated large-scale industrial problems through mathematical programming remains an unsolved issue.

1 Floudas, C.A., Lin, X., “Continuous-time versus discrete-time approaches for scheduling of chemical processes: a review”,..., 28, 2109-2129 (2004).

2 Shaik, M.A., Janak, S.L., Floudas, C.A., “Continuous-time models for short-term scheduling of multipurpose batch plants: a comparative study”,..., 45, 6190-6209 (2006).

3 Mendez, C.A., Cerda, J., Grossmann, I.E., Harjunkoski, I., Fahl, M., “State-of-the-art review of optimization methods for short-term scheduling of batch processes”,..., 30, 913-946 (2006).

4 Maravelias, C.T., Grossmann, I.E., “New general continuous-time state-task network formulation for short-term scheduling of multipurpose batch plants”,...., 42, 3056-3074 (2003).

5 Castro, P., Barbosa-Povoa, A.P.F.D., Matos, H., “An improved RTN continuous-time formulation for the short-term scheduling of multipurpose batch plants”,...., 40, 2059-2068 (2001).

6 Ierapetritou, M.G., Floudas, C.A., “Effective continuous-time formulation for short-term scheduling ·1· multipurpose batch process”,...., 37 (11), 4341-4359 (1998).

7 Giannelos, N.F., Georgiadis, M.C., “A simple new continuous-time formulation for short-term scheduling of multipurpose batch processes”,...., 41, 2178-2184 (2002).

8 Sundaramoorthy, A., Karimi, I.A., “A simpler better slot-based continuous-time formulation for short-term scheduling in multipurpose batch plants”,..., 60, 2679-2702 (2005).

9 Pan, M., Qian, Y., Li, X., “A novel precedence-based and heuristic approach for short-term scheduling of multipurpose batch plants”,..., 63, 4313-4332 (2008).

10 Pan, M., Qian, Y., Li, X., “Modified MILP model for scheduling of sequential multipurpose batch plants”,.... (), 57 (4), 861-866 (2006). (in Chinese)

11 Wu, J., He, X., Chen, B., Qiu, T., “A new continuous-time MILP model for scheduling of multi-product batch plants”,.... (), 54 (9), 1251-1256 (2003). (in Chinese)

12 Kondili, E., Pantelides, C.C., Sargent, R.W.H., “A general algorithm for short-term scheduling of batch operations. Part 1. MILP formulation”,..., 17, 211-227 (1993).

13 Pantelides, C.C., “Unified frameworks for optimal process planning and scheduling”, Foundations of Computer-aided Process Operations, Cache Publications, New York, 253-274 (1994).

14 Shah, N., Pantelides, C.C., Sargent, W.H., “A general algorithm for short-term scheduling of batch operations (II) Computational issues”,..., 2, 229-244 (1993).

15 Cerda, J., Henning, G.P., Grossmann, I.E., “A mixed-integer linear programming model for short-term scheduling of single-stage multiproduct batch plants with parallel lines”,...., 36, 1695-1707 (1997).

16 Mendez, C.A., Cerda, J., “An MILP continuous-time framework for short-term scheduling of multipurpose batch processes under different operation strategies”,, 4, 7-22 (2003).

17 Pinto, J.M., Grossmann, I.E., “Continuous time mixed integer linear programming model for short term scheduling of multistage batch plants”,...., 34 (9), 3037-3051 (1995).

18 Lamba, N., Karimi, L.A., “Scheduling parallel production lines with resource constraints (1) Model formulation”,...., 41, 779-789 (2002).

19 Mockus, L., Reklaitis, G.V., “Mathematical programming formulation for scheduling of batch operations based on nonuniform time discretization”,..., 21, 1147-1156 (1997).

2008-07-17,

2008-10-28.

the National Natural Science Foundation of China (20536020, 20876056).

** To whom correspondence should be addressed. E-mail: ceyuqian@scut.edu.cn