轨道交通引起的周边建筑物振动研究*

谢伟平，常 亮，谷 倩

(武汉理工大学土木工程与建筑学院，湖北 武汉 430070 )

交通荷载引起的周边环境振动已引起人们的广泛关注。交通荷载引起的环境振动评价问题，国内外学者已进行了大量的研究，但主要集中在交通荷载所引起的地面振动问题上，对周边建筑物振动问题研究的较少。

Hong Hao[1]分析了5种不同高度框架结构的水平向振动响应，将道路交通所引起的地面水平向振动加速度作为激励输入；S.H.Ju[2]研究了铁路桥梁附近建筑物的振动特性，计算结果表明，在影响房屋结构振动特性方面，列车荷载的频率比桥梁结构和列车自振频率更加重要；Adam[3]分析列车荷载作用下，铁路附近一栋6层(多层)钢筋混凝土框架结构的振动特性；曹艳梅[4]通过现场试验与数值分析的方法对运行列车引起的铁路线附近一栋12层 (高层)钢筋混凝土框架结构的振动特性及其影响因素进行了研究；王逢朝[5]通过数值分析的方法讨论了不同建筑物位置和基础埋深对列车引起的6层 (多层)框架结构建筑物振动的影响；Yao[6]使用有限元法，研究了一栋5层(多层)砌体结构的振动响应；夏禾[7-8]对铁路线路附近两栋2层 (低层)砖混结构的办公大楼各层楼板振动进行了现场试验，研究列车对邻近建筑物的振动影响；夏禾[9]分析了地面铁路、高架轻轨、地铁列车等轨道交通系统引起的周围环境及建筑物振动的基本规律；谢伟平[10]对公路、铁路、立交桥交通荷载共同作用下的广州环境监测中心9层(中高层)框剪结构形式的办公大楼各楼层的振动进行了监测。

根据作者的实测结果和其他研究者的研究成果[3-10]，整理归纳出：对于低层建筑，多层建筑，随着楼层的增高，振动强度有增大的趋势；对于高层建筑，随着楼层的增高，振动趋势表现出蜿蜒曲折的形状；有些情况下，楼层的水平向振动可能会大于竖向振动，在进行住宅建筑室内振动评价时，应根据具体情况，考虑水平向振动响应；由于各楼层的振动情况不同，应对各楼层的振动环境逐一进行评价。

从以上的结论，可知：与低层建筑和多层建筑不同，高层建筑各楼层的振动强度，并不是随着楼层的增高而增大。为了简化计算，本文仅以高架轨道所引起的房屋结构各楼层的竖向振动加速度响应为例，对高层建筑结构振动趋势产生的原因做了探究。

1 有限元模型的描述

1.1 房屋结构模型

使用ANSYS 三维有限元程序对房屋结构的振动响应进行了数值模拟。本文建立了4种不同建筑高度的混凝土框架结构模型，即18层+1层地下室，14层+1层地下室，10层+1层地下室，10层。图1是框架结构模型的标准层平面图和侧面图，这些模型横向有两个8 m的开间，纵向有4个8 m的开间，地面上部结构层高3 m，地下室层高3 m。前3种模型基础采用筏板基础，板厚2 m。第4种模型(10层)，采用柱下独立基础，在标高-0.3 m处设置基础拉梁。

次梁，内框架梁，外框架梁的尺寸分别为300 mm × 500 mm, 400 mm × 1 000 mm, 400 mm × 500 mm。柱的尺寸和配筋率列于表1中。

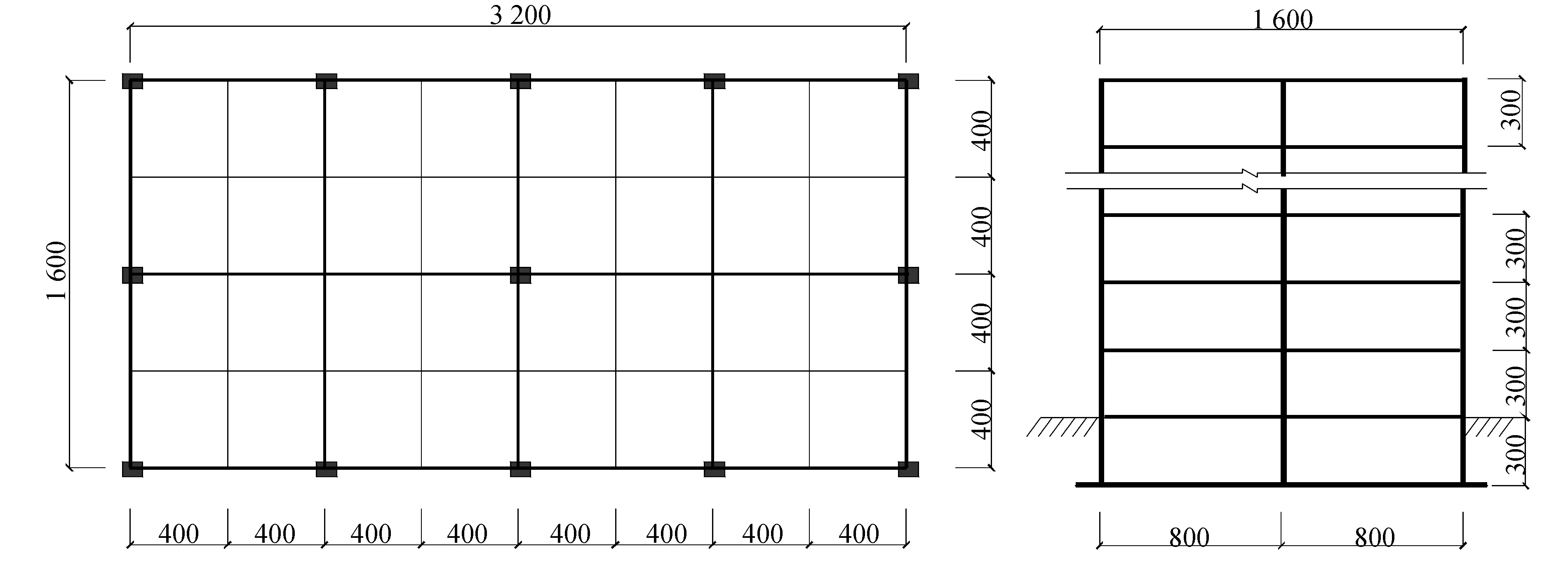
图1 结构模型 (单位：cm)

柱和梁采用2节点的三维线性有限应变梁单元，每个节点有3个平动自由度和3个旋转自由度。楼板和墙体采用4节点三维弹性壳单元，每个节点有3个平动自由度和3个旋转自由度。

1.2 土体模型

实际交通荷载所引起的地面振动可认为是一个半无限体，在用有限元法进行近场波动分析时，只能将感兴趣的部分人为地切割出来进行离散化，为了保证波动从切割区内部穿过人工边界时不会产生反射效应，在土体的截断边界处施加粘弹性人工边界，线性弹簧和阻尼分别模拟土体的弹性恢复力和辐射阻尼。线性弹簧的刚度和粘性阻尼系数[11-13]用下式表示：

表1 柱子尺寸和配筋率 mm×mm(%)

,CBT=ρcs

(1)

(2)

其中，KBT,KBN分别是切向弹簧刚度和法向弹簧刚度；CBT,CBN分别是切向阻尼系数和法向阻尼系数；R是振动源到人工边界的距离；cs,cp分别是剪切波波速和压缩波波速,G是土体的剪切模量；ρ是土体的密度；αT,αN分别是切向和法向人工边界的修正系数。文献[11]建议αT取0.67,αN取1.33。

土体参数列于表2中，由于交通荷载所引起的地面振动主要由表面瑞雷波组成，深层土体反射过来的体波成分非常微弱，上部土层对交通荷载引起的地面振动影响较大[1]，所以表2仅仅列出了前4层土体的参数。

表2 土体参数

土体的有限元模型尺寸是200 m×200 m×12 m。土体最大单元尺寸为2 m，土体使用8节点的三维实体单元模拟，每个节点有3个平动自由度。

1.3 激励输入

在桥墩刚性假定的基础上，将采集得到的地面上桥墩与土体接触处的振动加速度作为原始的激励输入。有限元模型如图2所示，F在房屋结构正前方20 m处。桥墩与土体接触处的振动加速度的傅氏谱和距离桥墩10 m处地面振动加速度傅氏谱如图3所示。

高架轨道交通所引起的地面振动，近场以高频成分为主，远场以低频成分为主。在距离轨道中心线20 m处，地面振动的频率成分主要集中在10～20 Hz[14]。为了减小计算规模并能合理地模拟振动波的传播特性，时间步长设为0.005 s，该时间步长大致是20 Hz振动波周期的1/10，并且单元最大尺寸控制在2 m，保证最大单元尺寸大致为20 Hz振动波波长的1/6，因此该模型能足够精确地模拟频率成分低于20 Hz的振动波。

图2 有限元模型

图3 地面振动加速度傅氏谱

该模型中采用瑞雷阻尼，其表达式为：

[C]=α[M]+β[K]

(3)

其中，[C]是整体阻尼矩阵；[M]是整体质量矩阵；[K]是整体刚度矩阵。对于土体和房屋结构，系数α和β的值分别为0.78 s-1和 3.7×10-4sm-1[2]。

2 数值结果和分析

本文仅仅定性分析房屋结构的振动，因此使用数值方法计算的振动加速度级不代表高架轨道交通引起的房屋结构振动的真实值。使用国际上普遍采用的振动加速度级，来分析房屋结构的振动。

对4种数值模型进行了模态分析和瞬态动力分析。各楼层点A(见图1)处的振动加速度级如图4所示；距离桥墩10 m处的地面振动加速度傅氏谱如图5所示。其中3种房屋结构模型的前5阶自振频率列于表3中。

图4 楼板竖向振动加速度级 (■18层; ▲14层; ★10层)

图5 距离桥墩10 m处模拟的地面振动加速度傅氏谱

2.1 模型的合理性

从图4，可以看出竖向振动加速度响应随着楼层号的增加，表现出蜿蜒曲折的形状。正如文献[4]所述，随着楼层号的增加，房屋结构楼板上的竖向振动的平均变化趋势是增大，减小，轻微增大，但是在20组实测的振动加速度级变化曲线中，每一条曲线都表现出不同的形状。因此，与实测结果相比[4]，本文的数值模型是可靠的，数值模拟的结果能够反映房屋结构楼板的振动加速度响应随楼层号的增加而表现出的变化趋势。

比较图3(b)和图5，在距离桥墩10 m处，模拟的地面振动加速度谱与实测结果非常相似，曲线的大体形状相似，并且峰值所对应的频率也大致相同，说明土中每一振动波的衰减情况基本上与实际情况一致。因此，可以证明在模拟振动波的衰减情况方面土体模型和激励力的输入是可靠的，同时保证了房屋结构的激励输入是正确的(因为房屋结构的振动是由土体振动引起的)。

2.2 自振频率对房屋结构振动的影响

表3 房屋结构模型的前5阶自振频率

表3中的数据表明，对于同种结构布置形式的框架结构，随着建筑高度的降低和楼层数的减少，结构的自振频率一般会增大。

对于这3种框架结构，10层带1层地下室的房屋结构前3阶振动模态中，楼板基本是以横向振动为主，在第四阶振动模态中，楼板出现明显的竖向振动，其它两种房屋结构则是在第五阶振动模态中，楼板出现明显的竖向振动。

结合图4，3种房屋结构，楼板竖向振动加速度级的变化趋势表明，楼板的振动随着建筑高度的降低和结构自振频率的升高不是单纯地递增或递减。在较低层，楼板振动受结构的自振频率影响较小，但是在较高层，这种影响变得明显，楼板的振动随着房屋结构自振频率的升高而加强。

2.3 振动放大区域的存在

在波的传播过程中，当其遇到波屏障时，在两种弹性介质的分界面处发生波的反射与折射,一部分瑞雷波和体波作为能量输入到结构中，其余的瑞雷波被反射回土体中，与入射波相互叠加；其余的体波被迫沿着屏障向下传播。实际结构中，地下室剪力墙，基础拉梁与地下部分墙体充当着波屏障的作用。如图6，图7所示，图中相邻两测点之间的距离是1 m，测点1距离桥墩10 m。

在建筑物前3 m的范围内，如图7所示，地面振动随着距轨道中心线距离的增加，衰减变得缓慢，甚至出现轻微增大的趋势，也就是说，在建筑物前3 m的范围内，反射波对地面振动有一定的影响，导致了地面振动比没有建筑物时地面振动大。

图6 有限元模型中测点的布置 (◆测点，单位：cm)

图7 地面振动和第一层楼板振动 (○ 10层带1层地下室; ■10层)

而且，可以发现，存在地下室时，建筑物前3 m的范围内的地面振动比不存在地下室时，地面振动要大，这主要是由于屏障深度的影响(地下室剪力墙形成的屏障深度比基础拉梁与地下部分墙体形成的屏障深度要大)。

在第一层楼地板区域，如图7所示，存在地下室时，第一层楼板的竖向振动，明显大于不存在地下室时楼板的竖向振动。并且相比于建筑物前部地面振动，存在地下室时，楼地板的竖向振动明显放大；不存在地下室时，楼地板振动明显减小。基于这些发现，可以说，在入射波的作用下，本来地基土各点的运动是不同的，但是由于基础的约束，使得各点运动符合刚体运动关系，也就是地基土的刚度被加强，并且第1层楼板受到地基土的约束，因此不带地下室的房屋结构第1层楼板的振动比带地下室的房屋结构第1层楼板的振动小。同时，可以发现，不存在地下室时，测点12处楼地板的振动(房屋内部第一层楼板上的测点)明显衰减，主要是因为波屏障阻碍了波的传播(墙体1对波的阻碍，见图6)，并且从测点24到测点27，楼地板的振动有轻微的反弹增大趋势，这是入射波与反射波相互叠加的结果(墙体2对波的反射，见图6)。注意到，存在地下室时，测点19处楼地板的振动(对应于图1中的测点A)明显低于相邻两测点的振动，这是因为，测点19处于两内框架梁的交点处(见图1)，该处的约束比其它测点处的约束要强。

在建筑物后部区域，如图7所示，由于波屏障(地下室剪力墙，基础拉梁与地下部分墙体)对振动波的阻碍，测点28处的地面振动有明显的衰减。存在地下室时，地面振动强度略高于不存在地下室时地面振动，导致该现象发生的原因可能是由于不存在地下室时，第一层楼地板下的部分土体受到基础、柱、基础拉梁的共同约束，起到了波屏障的作用，其隔振效果比地下室剪力墙的隔振效果好。

2.4 最大的振动加速度响应

在2.1节中，指出对于高层建筑物，高架轨道交通所引起的楼板最大竖向振动加速度响应发生在中间的某一层而不是在顶层。本节将对这一问题进行讨论。首先，在1.1节中18层框架模型的基础上，通过施加阻尼装置，建立了两种修改模型：一种模型是在18层层顶施加阻尼装置，另一种模型是在12层层顶施加阻尼装置。土体模型和激励力保持不变。数值模拟结果如图8，图9所示。

从图8可以看出，与18层框架结构模型相比，当阻尼施加在18层层顶的时候，各层楼板的振动加速度级从14层到18层都有一定程度的减小。从图9可以看出，当阻尼施加在12层层顶的时候，相邻各层楼板的振动加速度级都有明显的减少，尤其是在第13层。

可以这样理解，当振动波到达楼板时，一部分的振动能量被楼板的阻尼所消耗掉，另一部分的振动波能量沿着梁柱向上向下传递到相邻楼板，但是当楼板的振动能量被阻尼耗散掉后，传递到相邻楼板的振动能量将会减少，因此相邻楼板的振动响应将会降低。这种现象表明，高层建筑结构各部位的振动情况较为复杂，各层楼板的振动是入射波与反射波相互叠加的结果。同时，注意到6层以下(低层，多层)楼板振动受反射波的影响较小，因此，不难理解，低层建筑，多层建筑，随着楼层的增高，振动强度有增大的趋势；但对于高层建筑结构，其最大的振动加速度响应发生在房屋结构的某一中间层。

图8 模拟的楼板振动加速度级 (■18层;○阻尼加在18层层顶)

图9 模拟的楼板振动加速度级 (■18层;△阻尼加在12层层顶)

3 结 论

(1)对于低层建筑，多层建筑，随着楼层的增高，振动强度有增大的趋势；对于高层建筑，随着楼层的增高，振动趋势表现出蜿蜒曲折的形状；有些情况下，楼层的水平向振动可能会大于竖向振动，在进行住宅建筑室内振动评价时，应根据具体情况，考虑水平向振动响应；由于各楼层的振动情况不同，应对各楼层的振动环境逐一进行评价。

(2)对于高层建筑，楼板的振动随着楼层号的增加，不是单纯地增大或减小，最大的振动响应可能发生在中间的某一层，这是由于入射波与反射波相互叠加的结果，从实测与计算结果也证明了这一点。

(3)对于相同结构布置形式的框架结构，随着建筑高度的降低，结构的自振频率一般会增大，但是各层楼板的竖向振动加速度级不是单纯地增大或减小。在较低楼层，自振频率对楼板的竖向振动影响较小；但是，在较高楼层，自振频率的影响较大，也就是说，在较高层，楼板的竖向振动加速度响应随着房屋结构自振频率的增大而加强。

(4)由于基础约束的影响，不带有地下室的房屋结构，其第一层楼板的振动加速度响应会比带地下室的房屋结构第一层楼板的振动加速度响应要小。

(5)由于波的反射与叠加，在房屋结构前会存在一个振动放大区域。

参考文献：

[1] HONG H. Building vibration to traffic-induced ground motion[J]. Building and Environment, 2001, 36(3): 321-336.

[2] JU S.H.. Finite element analysis of structure-borne vibration from high-speed train[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(3): 259-273.

[3] ADAM M., ESTORFF O.von. Reduction of train-caused building vibraiotns by using open and filled trenches[J]. Computer and Structures, 2005, 83: 11-24.

[4] 曹艳梅, 夏 禾, 战家旺. 运行列车引起高层建筑物振动的试验研究及数值分析[J]. 工程力学, 2006, 23(11): 182-187.

CAO Yanmei, XIA He, ZHAN Jiawang. Experimental study and numerical analysis of moving train induced vibrations on high-rise buildings[J]. Engineering Mechanics 2006, 23(11): 182-187.

[5] 王逢朝, 夏 禾, 吴 萱. 列车振动对周边环境及建筑的影响分析[J]. 北方交通大学学报, 1999, 23(4): 13-17.

WANG Fengzhao, XIA He, WU Xuan. Vibration effects of trains on surrounding environments and buildings[J]. Journal of Northern Jiaotong University, 1999, 23(4): 13-17.

[6] YAO J. B., Xia H., CHEN J. G.. Study on dynamic response laws of building under train actions[C]//Yang Y.B. and Yau J.D.. Proceeding of the 3th International Symposium on Environmental Vibrations: Prediction, Monitoring and Evaluation. Taipei, China: Department of Civil Engineering, National Taiwan University, 2007: 210-215.

[7] XIA He, ZHANG Nan, CAO Yanmei. Experimental study of train-induced vibrations of environments and buildings[J]. Journal of Sound and Vibration, 2005, 280(3/5): 1017-1029.

[8] XIA He, CAO Yanmei, HAN Yan. Traffic-induced environmental vibrations and their influences on surrounding buildings[C]//CHEN Yun-min, TAKEMIYA Hirokazu. Proceeding of the International Seminar on Environmental Vibration: Prediction, Monitoring and Evaluation. Hangzhou, China: China Communications Press, 2003: 230-241.

[9] 夏 禾, 曹艳梅. 轨道交通引起的环境振动问题[J]. 铁道科学与工程学报, 2004, 1(1): 44-51.

XIA He, CAO Yanmei. Problem of railway traffic induced vibrations of environments[J]. Journal of Railway Science and Engineering, 2004, 1(1): 44-51.

[10] YU Yanli, XIE Weiping. The vibration measurement and evaluation due to the traffic loads[C]// CHEN Yun-min, TAKEMIYA Hirokazu. Proceeding of the International Seminar on Environmental Vibration: Prediction, Monitoring and Evaluation. Hangzhou, China: China Communications Press, 2003: 427-431.

[11] 谷 音, 刘晶波, 杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元[J]. 工程力学, 2007, 24 (12): 31-37.

GU Yin, LIU Jingbo, DU Yixin. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007, 24 (12): 31-37.

[12] DEEKS A J，RANDOLPH M F. Axisymmetric time-domain transmitting boundaries[J]. Journal of Engineering Mechanics, ASCE, 1994, 120(1): 25-42.

[13] 谢伟平, 常 亮, 杜 勇. 中南剧场隔振措施分析[J]. 岩土工程学报, 2007, 29(11): 1720-1725.

XIE Weiping, CHANG Liang, DU Yong. Analysis on vibration isolation of Zhongnan Theater[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1720-1725.

[14] 张 昕. 高架轨道交通引起环境振动的实测和理论分析研究[D]. 上海: 同济大学土木工程学院, 2002.

ZHANG Xin. Practical and theoretical research on the environmental vibration caused by elevated railroad traffic[D]. Shanghai: School of Civil Engineering, Tongji University, 2002.