加强画图训练,提高解题能力
2009-05-07郭载芹
郭载芹
小学数学应用题既是教学中的重点,也是教学中的难点,有不少的应用题,文字叙述比较抽象,数量关系比较复杂,小学生的思维又处于具体形象思维向抽象逻辑思维的过渡阶段,对于一些抽象问题理解起来困难较大.如果教师一味的从字面去分析题意,用语言来表述数量关系,虽然老师讲的口干舌燥,学生却难以理解掌握,事倍功半.即使是学生理解了,也只是局限于会做某个题了.俗话说,授之以鱼,不如授之以渔.一个教师不仅要教给学生知识,更重要的是交给学生学习知识的方法.线段图在小学数学应用题教学中起到了奇妙的作用,它可以帮助学生轻松、愉快的学会复杂关系的应用题,既培养了学生的能力,又促进了学生了思维的发展,是教学中行之有效的教学方法.
一、利用线段图让学生口头编应用题
从中低年级培养,从简单题入手,是培养学生画图能力的基础.
线段图的及时引入,是帮助学生揭示数量关系和掌握解题思路的一种好方法.在教一年级数学时,我就对学生进行认识线段图和根据线段图口述应用题的训练,取得了较好的教学效果.这个时候教师的指导、示范、点拨是培养学生画图能力的关键.学生刚学习画线段图,不知道从那下手,如何去画.教师可以指导学生跟教师一步一步来画,找数量关系.也可以教师示范画出以后,让学生仿照重画一遍,即使是把老师画的图照抄一边,也是有收获的.
在第一册刚讲应用题时,我就引导学生逐步学会识图.如:黄花有6朵,红花有5朵,黄花和红花一共有多少朵?我先用直观教具讲解了这道题,使学生明白求红花和黄花一共的朵数,就是要把黄花和红花的朵数并起来.然后我再引导学生把直观教具图转化为线段图.提问:如果老师用线段来表示黄花和红花的朵数,要画几条线段?能画一条线段吗?为什么不能只画一条?画线段图时,两条线段能画一样长吗?为什么?表示什么花的要画得长些?为什么?根据学生的回答,完成线段图:

从而列出算式:6+5=11(朵).讲好后我没有就此作罢,而是把这一道题编成一道减法应用题:黄花和红花一共有11朵,其中黄花有6朵,红花有多少朵?我通过问题引导学生回答出:这题是用一条线段表示一共11朵,再在这条线段上标一段表示黄花的6朵,剩下的是要求的红花有几朵:
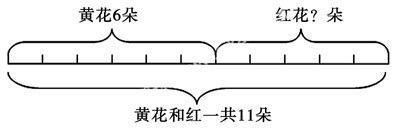
列式:11-6=5(朵)
通过这样的训练,学生逐渐认识了线段图,对线段图能帮助理解题意有了朦胧的认识.这以后,在教学中,我就经常画一些线段图,让学生看图口述成应用题.如:

这样,从低年级起,就通过线段图对学生进行口述应用题的训练,然后逐渐培养学生学会画线段图,通过线段图分析理解题意,这就为以后学好复合应用题打下了坚实的基础.线段图的培养一定要从中低年级培养,从简单题入手,从小养成画图解题的意识和良好的画图技能技巧.
二、引导学生通过画线段图解答复合应用题
学生有了低年级线段图的训练的基础,到了中高年级学习两三步计算的应用题时,就能在老师的引导下,正确应用线段图,使数形结合,解决问题.此时,要求学生边画边讲,或互相讲解.教师对有困难的学生一定要给以耐心的指导.学生掌握了一定的技能后,教师可以放手让学生自己去画,教师给以适时的点拨,要注意让学生讲清这样画图的道理,可自己讲,也可分组合作讲.教师一定要让学生体会用图解题的直观,形象,体会简洁、方便、易理解的特点,提高应用的自觉性、主动性.
如:少先队员种杨树45棵,种杉树的棵数比杨树的3倍少9棵.种杉树多少棵?教师引导学生找出解决问题的关键条件:种杉树的棵数比杨树的3倍少9棵,画出线段图:
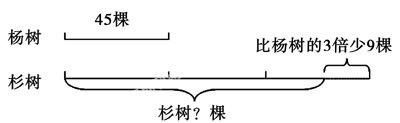
从而列出算式:45×3-9=126(棵)
其实,只要学生掌握了画线段图的方法,那么解决两三步运算的应用题就并不显得难了.如上题,到了四年级下学期又可以变成列方程解的应用题:同学们栽杉树126棵,比杨树的3倍少9棵.栽杨树多少棵?这题所画的图和上一题其实是一样的,只不过杨树的45棵换成了x棵,从而列出方程:
解:设栽杨树x棵.
3x-9=126
特别是到了高年级,借助于画线段图来直观表示题目中的已知条件和问题,帮助学生理解题目的数量关系,有助于解答比较复杂的分数应用题,当然编者在编教材时也注意通过图形结合来培养学生的解题能力.有了坚实的基础后,到高年级时学生对此能如鱼得水,应用自如.
三、通过线段图进行变式练习,开拓思维
学生有了一定的画图解题能力后,老师更加要注意引导,教师要指导学生画图重点做到以下几点:(1)认真读题,全面理解题意,所画的图要与题目中的条件相符合.(2)图中线段的长短要和数值的大小基本一致,不要长的线段标出小的数据而短的线段标出大的数据.图要画的美观、大方、结构合理,具有艺术性.(3)要按照题目的叙述顺序,在图上标明条件.对于双线段并列图和多线段并列图一定要分清先画和后画的顺序,要找准数量间的对应关系,明确所求的问题.这是分析题意和列算式的重点,需要进行大量的训练才能提高分析问题和解决问题的能力,并非一日之功.
我就经常通过变式练习,让学生的解题能力在画图和练习时得到进一步的提高,思维得到进一步的发展.如:一个乡去年原计划造林12公顷,实际造林14公顷.实际比原计划多百分之几?老师稍一提示,学生会很快地画出图来.此题解答后,教师不妨出示变化了的图:

先让学生口述成应用题,再比较这两题的异同,然后解题.通过师生的双边活动,学生的思维得到开拓.这时老师可以让学生自己进行变式,画出线段图,编出应用题.如:
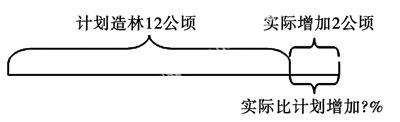
这样,教师遵循学生的认知规律,万变不离其“图”,从“口述”到“画图”和变换角度思考,在对比练习中,开拓了学生的思维,发展了学生的智力,培养了学习品质,把学生引入学习知识发展能力的良性循环中,解题的能力逐步得到提高,对一些思考题也就不觉得那么难了.
知识的拓展和迁移,是线段图应用的难点.线段图的而应用还可以迁移到其他类型的题.掌握一个解题方法,比做一百道题更重要.实践证明,线段图具有直观性、形象性、实用性,如果学生从小掌握了用线段图辅助解题的方法,分析问题和解决问题的能力将会有大大的提高,对今后的学习生活将有很大的帮助.
