例谈北师大版第10册《长方体(一)》教学难点的处理
2009-04-21徐曦霞
徐曦霞
一、纵横联系——长方体认识的拓展
魔方涂色:如“一个棱长为3厘米的正方体,六个表面都涂上红色。将这个正方体切成棱长为1厘米的小正方体后,三面涂红色的有()个,两面涂红色的有()个,一面涂红色的有( )个,没有涂红色的有()个。”此道题目让学生靠想象,答案很难准确。动手操作,麻烦,耗时耗力,对思维帮助不大。教师自己则应深入研究此题的编排目的,既不是为了让每个孩子都动手操作,也不是为了让大家都来记忆这样的题目,而是通过这样的练习,加深对正方体特征的理解,及在生活中的简单。
法国大文豪雨果给我们启发:“没有一种心理机能比想象力更能深化自我,更能深入对象。科学到了最后的阶段,就遇到想象。”通过画图,思考,与正方体的特征联系起来,就发现其实十分简单、形象,易理解。三面涂红色的都在顶点的位置,那么一个正方体有8个顶点,每个顶点对应一个,自然有8个三面涂红色的小正方体;两面涂红色的位置都在棱的中间,而且两个红色的面刚好是在棱的两侧,那么一个正方体有12条棱,答案就是12个;同理,一个面涂红色的位置,都在每一个面的正中间,它的数量自然与面的数量是相等的;而通过想象或计算都可以知道,还有一个小正方体,在这个大正方体的中间。如果看成一个魔方的话它就是魔方的轴心,当然只有一个啦。
进一步研究会发现,只有在表面的小正方体才可能着色,而里面的都不可能着色,这点学生很容易理解。那么,由此引申开去,就可以推导出:将一个正方体或长方体的表面涂上颜色后,无论将它平均切成多少个小正方体,三面着色的都只能有8个,因为顶点的个数不变:而两面着色和一面着色的数量都会是12和6的倍数,具体的只要通过画出一面的图就可以计算得出;没有着色的只要用总数减去前面三部分的就可以算出。
二、虚实相映——展开与折叠的运用
展开与折叠是新增部分,老师在教学时不易把握教学关键,容易将这理解为求表面积所作的铺垫。笔者认为这样的定位误解了教材的编排意图,作铺垫是目的之一,但更重要的是通过展开与折叠的活动,沟通平面与立体图形之间的联系,有效促进学生空间观念的形成。教学中,除了让学生动手去操作外,还应引导学生在操作中体验,在体验中发现其中的规律。如下图(课本第16页的练习),判断哪些平面图形能折成正方体?
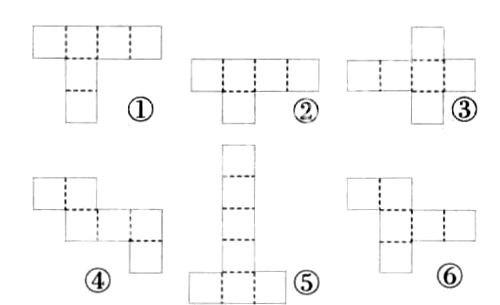
先确定正方体剪开后的基本图形是图③,周围4个面加上下各一个面,比较直观,学生容易理解,基本形通过平移还可以得到上图的形状;再看图④和图⑥,其中的一个正方形绕一个点,旋转90度后能变成基本图形,所以能够折成正方体。图②和图⑤的面数不对,一定无法折成正方体;而图①无论旋转哪个正方形都不能得到基本图形,也无法折成正方体。原则是:相对的面不相连,相连的面不相对。
再如下图:
①要剪开几条棱,才能成目前的展开图。
②折成正方体后,1、3、4的对面分别是几?
③集结于同一个顶点的三个面的数的乘积最大是多少?
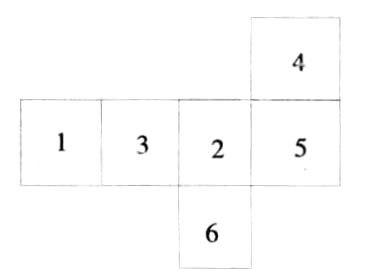
第一个问题要用逆推法,没剪开的棱有5条,12条棱减去5条没剪开的,当然是剪开了7条;第二个问题相对的两个面,中间一定要经过一个面,他们不相连,所以l对2,3对5,4对6;第三个问题是如何根据展开图上的数据计算,因为相对的面不会集结于同一个顶点,所以从第二个问题的答案三组数中各找出较大的2,5,6,相乘后得到60。
三、物形互补——露在外面的面
这部分知识重在规律研究,空间想象的培养。首先是面的平移:如在一个棱长为5厘米的正方体的一个顶点处挖去一个长3厘米、宽2厘米、高1厘米的长方体,表面积是()?很多学生会想当然地认为,一个正方体的表面积,减去一个长方体的三个面面积的差。其实从面的平移可以知道,切割后的表面积并没有变化,道理与楼梯形状的周长的计算相同。
照下面的样子,将正方体堆放在墙角,放三层共有几个正方体?露在外面的面有几个?四层呢?五层呢?填入下表,观察一下,有什么规律?
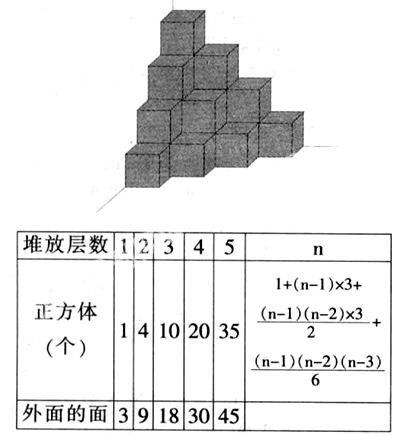
从上往下数
方法一:五层竖看 正方体个数
看得见下有层数
第一层:1个 ×5层=5个
第二层:2个 ×4层=8个
第三层:3个 ×3层=9个
第四层:4个 ×2层=8个
第五层:5个 ×1层=5个
共35个
规律:有几层,就将每一层看得见的个数乘层数,即可得所用正方体总个数;用看得见的部分的正方体个数相加的和乘3,可得露在外面的面的总数。
方法二:五层横看 正方体个数
看得见 看不见
第一层: 1 +0=1
第二层: 2 +1=3
第三层: 3 +3=6
第四层: 4 +6=10
第五层: 5 +10=15
规律:将看得见与看不见的两部分相加,可得所有正方体总个数;再用看得见的正方体的个数乘3,即可得露在外面的面的总数。
