基于混合法的内部结构声分析

彭伟才 赵高煜 何 锃

华中科技大学力学系，湖北武汉430074

基于混合法的内部结构声分析

彭伟才 赵高煜 何 锃

华中科技大学力学系，湖北武汉430074

有限元法（FEM）是广泛接受的分析耦合结构声（SA）系统动力响应的预报工具。由于随频率增加计算模型也增加导致基于单元的方法在实际中约束在低频段。一种替代方法是基于间接Trefftz法的基于波动方法（WBM）。但WBM的不足之处在于高计算效率只针对中度复杂的几何模型。为了利用两者的优势：FEM的广泛应用和WBM的高收敛特性，提出了混合FE－WB预报法（FEM－WBM）。基本原理是将FE模型中较大且几何简单的部分采用WBM代替。得到的耦合模型仍具有较少的自由度。简要描述了FEM、WBM以及混合FEM－WBM的理论基础。最后将该方法应用于一个简单的结构声模型，理论分析结果与数值仿真计算结果吻合较好，该混合方法有潜力覆盖中频段。

结构声分析；直接耦合；混合方法；基于波动方法；有限元法

1 引言

封闭空腔内的噪声主动控制问题具有重要的工程应用背景，如土木、工业和防御设施等场所的降噪。有源结构声控制（ASAC）［1－3］，来自噪声有源控制（ANC），利用结构的振动作为次级声源来消除初级声源产生的声场。然而封闭空腔声场主动控制的理论研究中涉及到的一个基本问题是结构声耦合作用。在噪声的主动控制中，许多工程问题如汽车驾驶室、飞机机舱等都简化为简单形状的声腔由弹性结构包围。耦合结构振动和声场构成振动声系统。

过去通常采用解析和实验的方法研究结构声问题。早期的研究者如 JUNGER，FEIT［4］和DOWELL等［5］发展了一种基于模态理论框架的内部声场预报方法。自从那以后许多研究者致力于研究结构声耦合问题，提出了能量法、格林函数法、声弹性法、覆盖域法和数值方法等。

能量法，如SEA或者EFM［6］，不适合低频以及不能提供封闭空腔内声压分布的详细信息。

另一种方法称之为声弹性法［7］，该方法需要采用FEM来得到非耦合结构的单个模态信息和刚性壁声腔的声场。然后将两者进行耦合最后得到结构声耦合方程。实验证明该方法计算效率比较高。虽然其也可以应用于较复杂腔体的分析，然而得到复杂腔体的模态信息目前仍要借鉴试验手段或有限元法。

LUO等［8］提出了格林函数法。该方法根据模态叠加原理，从格林函数的观点出发，结合流体的波动方程和结构振动方程，导出了系统的声压和速度响应表达式。虽然摆脱了对模态解析解的依赖，但是模态叠加法导致计算收敛速度非常慢以及精度低。

WU等［9］提出了可以预报任意形状声腔内部声场的解析法。覆盖域法结合流体波动方程和结构振动方程，应用声学互易原理，给出了封闭腔体在外力作用下其内的声压分布解析解。球谐函数展开的解析式进行数值计算时，收敛很慢，尤其在kR（k为波数，R为覆盖球半径）稍大时，需计算相当多的级数项以达到较高的精度。球谐函数中（n-m）！／（n＋m）！的高阶因式分解通常难以达到计算要求的精度，有时甚至得不到计算结果。ZHANG和CHEN［10］对该方法的精度和效率进行了改进。

现今广泛应用的有限元和边界元（BE）也存在一些缺点：FE存在发散现象；而BE因为其复数、非对称矩阵需要大量的计算时间。

一种替代方法是由DESMET［11］提出的WBM。VAN HAL［12］提出了基于声压和速度连续的间接耦合方法，并且已经成功应用到了二维的声问题。由于引入了自由度框架，间接耦合模型增加了额外的自由度。本文主要讨论直接耦合方法。我们已经利用该方法完成了耦合振动声系统建模分析［13－16］。

本文描述了三维耦合振动声系统建模方法的基本概念。分别讨论了FEM和WBM的理论背景。最后通过混合FE－WB模型算例对该方法进行了讨论。

2 基本定义

图1所示为3D结构与声耦合模型。声域V的边界 Ωa包括 4个部分（Ωa＝Ωp∪Ωv∪ΩZ∪Ωs）。在边界Ωp，Ωv和ΩZ分别为压力、法向速度和法向阻抗边界条件，而边界Ωs由弹性平板组成，平板的边界为Гs。腔内充满密度为ρa和声速为c的流体。板材料属性为：密度为ρs，泊松比为v，弹性模量为E和材料损耗因子为η。法向集中力F作用在板的rF′（xF′，yF′）处。

域V内任意点r（x，y，z）的声压p由赫母霍兹方程控制。

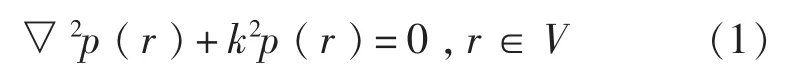
图1 三维结构与声耦合模型

考虑到集中力F以及声压的耦合作用，板的法向位移w（x′，y′）控制方程为：

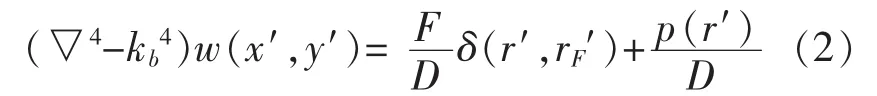
其中，p（r′）为作用在板上的腔内声压。该载荷只影响板的横向位移，所以结构声耦合效应转换成式（2）中的额外载荷项，它正比于“湿”表面上的声压。

耦合结构与声问题的边界条件。

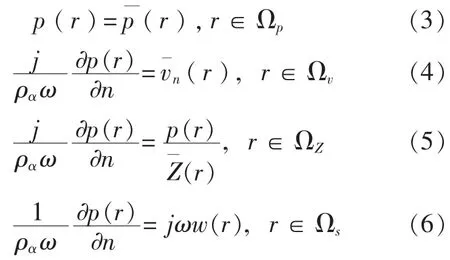
其中，p（r）为已知压力函数，vn（r）为已知法向速度函数，Z（r）为已知法向阻抗函数以及w（r）为弹性边界上的法向位移；n为边界法向（规定由内向外为正方向）。板的边界ΓS存在两类边界条件：

边界Γw上为运动学边界条件。

边界Γt上为力学边界条件。

其中，w（r′）和T（r′）分别为边界上已知横向变形分量和力分量。

3 FEM和WBM回顾

3.1 FEM分析结构声系统

考虑声压场p和位移场w由局部定义的基函数 Na和 Ns的展开式来近似［12］。

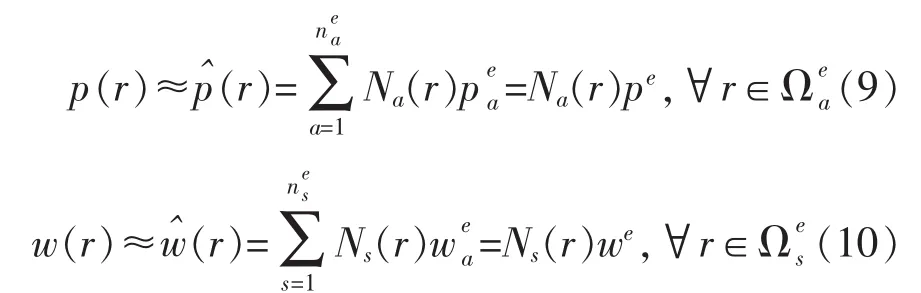
引入的误差通过积分的方法使其为零，将式（3）～式（8）分别转换到声腔和结构对应的加权余量公式中。

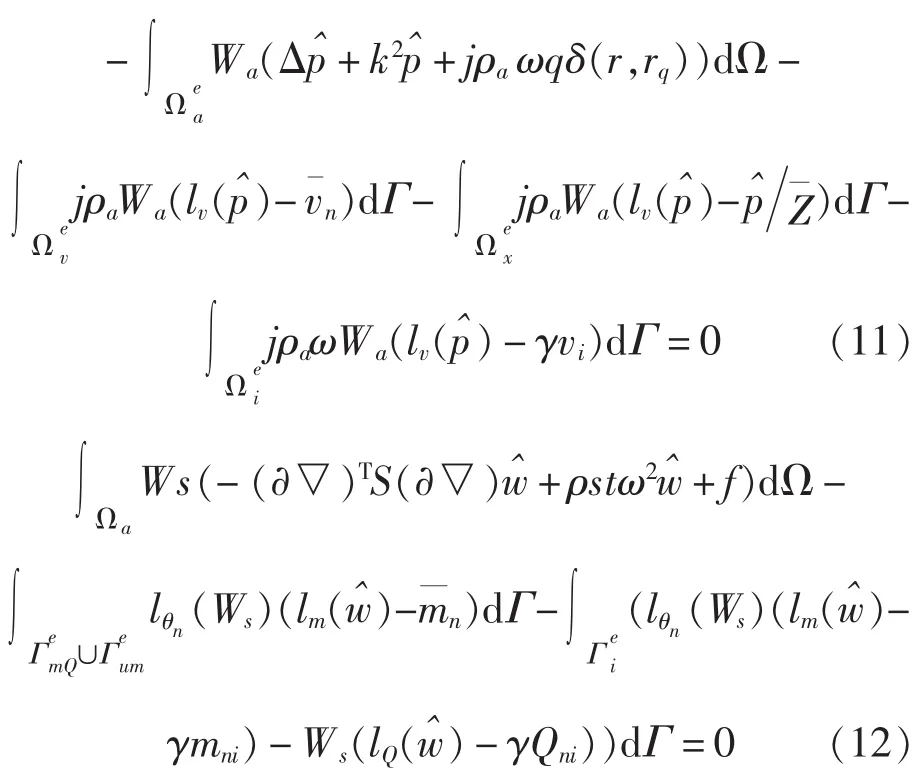
其中，Wa和Ws为加权函数。

将近似函数和加权函数代入式（11）～式（12）得到下列FE模型。

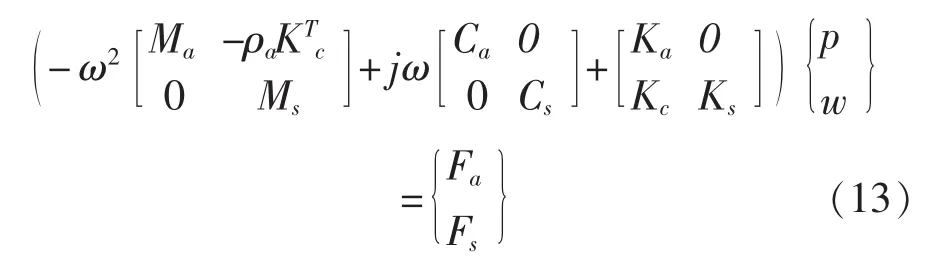
其中，Ks和Ka，Cs和 Ca，Ms和Ma分别为结构和声的刚度矩阵、阻尼矩阵和质量矩阵。Fs和Fa为结构和声的外部节点向量。Kc为耦合项。耦合刚度矩阵和质量矩阵都是与频率无关的，但与非耦合的模型相比，这些耦合矩阵不再是对称矩阵。主要因为流体对结构的载荷正比于声压，导致了耦合刚度矩阵中出现交叉耦合矩阵Kc；而结构对流体的载荷正比加速度，导致了耦合质量矩阵中出现交叉耦合矩阵－ρaKTc。

3.2WBM分析结构声系统

WBM采用满足控制方程的近似函数。近似函数由满足式（1）～式（2）的全局定义基函数Фa和Ψs以及考虑外部激励的特解函数组成［12］。

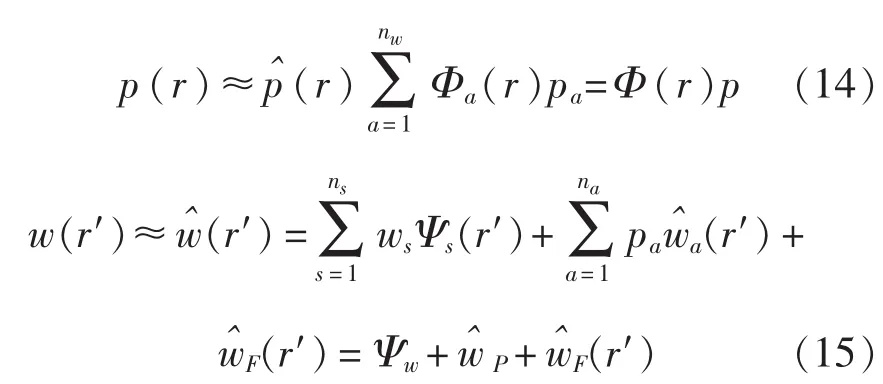
其中，未知系数pa构成向量p以及ws构成向量w。

声学边界条件的加权余量公式

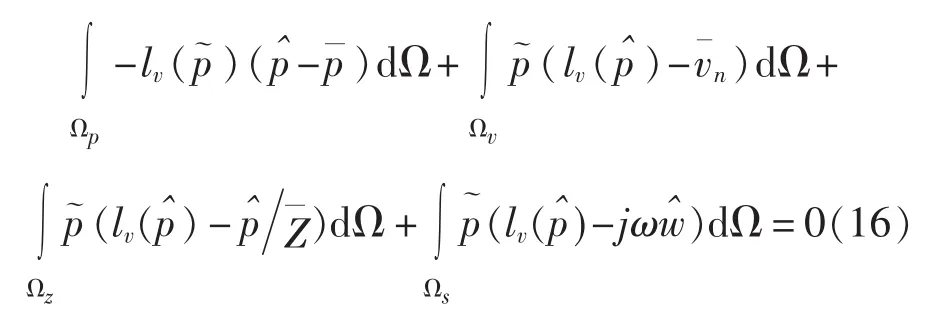
结构边界条件的加权余量公式

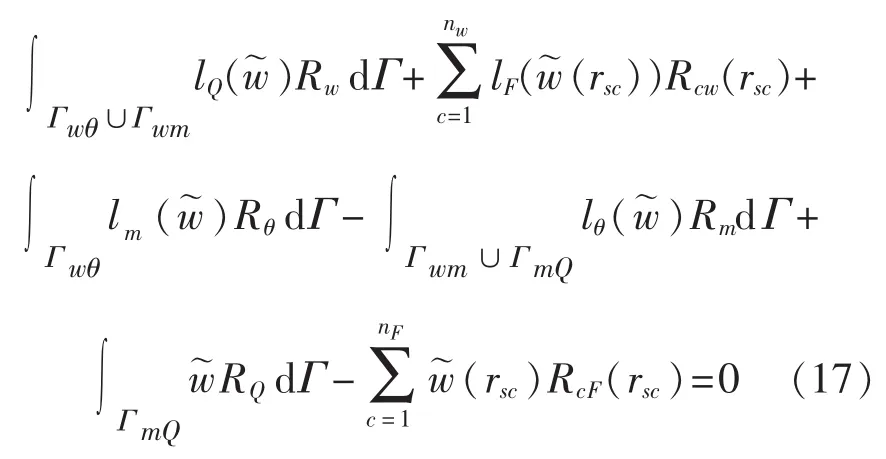
联立式 （16）～式（17）得到结构声模型

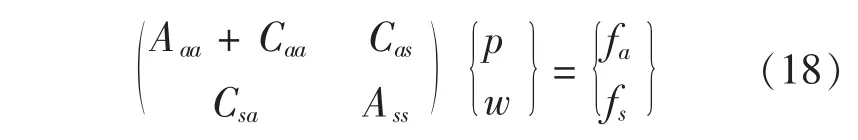
求解式（18）中的未知系数pa和ws，然后带入式 （14）～式（15）得到整个系统的振动响应结果。

4 耦合FEM－WBM

耦合FEM－WBM试图结合FEM和WBM各自的优势，即WBM的高收敛特性和FEM对任意几何形状的适应能力。在实际中通常一个简单形状的声腔由复杂的弹性结构包围。对于比较简单的结构WBM可以处理，但是对于比较复杂的结构采用FEM比较适合。而声腔可以采用几何形状比较简单的一个或者多个WB子域建模。当然也可以采用FE离散，但为了达到较好的精度在临近湿表面的声腔需要非常细的网格。本文主要讨论直接耦合法，即在WB域和FE域的界面ΩH同时引入连续性边界条件，其中Ω为界面上的FE单元域，图2为直接耦合法的示意图。

图2 直接耦合法

在耦合FE－WB模型中，结构振动和声压场的直接耦合可以通过声模型的强制速度连续性条件（6）和在结构方程中引入声压载荷来实现。耦合FE－WB模型采用非耦合方法中结构位移和声压的场变量展开式。在耦合方程中引入展开式可以得到一组直接联系两个物理域自由度的代数展开式。FE域的加权余量公式增加了作用到结构上的声压载荷。在WB方程（16）中引入结构声耦合界面ΩH上的速度连续性条件的加权余量公式。

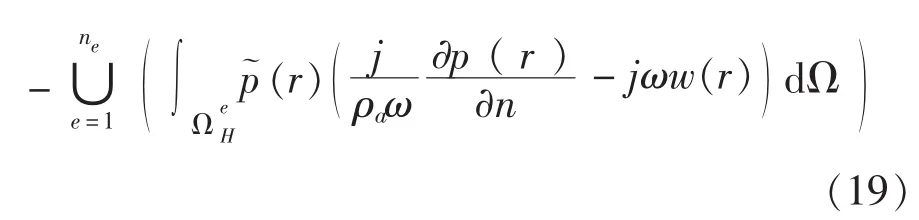
其中，ne为界面单元数。

联合两个域的加权余量公式，应用伽辽金方法代入加权函数 p~（r），最后组装FE域就可以得到整个系统关于节点结构位移分量w和波函数系数p的矩阵方程。

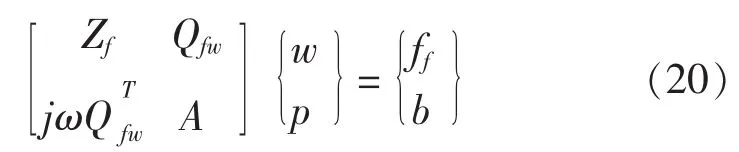
其中，Zf和ff为FE系统矩阵；A和b为WB系统矩阵。耦合矩阵Qfw定义为：

其中，Nf为FE形函数，Φ为WB波函数。

矩阵Zf是FE系统矩阵，它是对称、稀疏和有限带宽矩阵。矩阵A是WBM的系统矩阵，它是稠密矩阵，但一般要比矩阵Zf小（nw＜＜nf）。因为只有FE节点自由度位于界面ΩH上而应用波函数到与界面相邻的WB域得到的是非零矩阵系数，所以耦合矩阵Qfw是稀疏的长方矩阵。对于这类复杂的方程需要经过特别处理才能求解。

5 数值算例与分析

计算模型为如图3所示系统。域的特征尺寸为 Lx＝0.5 m，Ly＝0.5 m，Lz＝0.75 m，Lzm＝0.5 m，Lxm＝0.25 m。声腔中充满空气，密度ρa＝1.225 kg／ m3，声速c＝340 m／s。其中弹性结构为铝板：泊松比v＝0.3，弹性模量E＝7×1010N／m2，密度ρs＝2 790 kg／m3，材料损耗因子η＝0，厚度t＝2×10－3m。其余边界条件为刚性壁 vn＝0 m／s。单位力F作用点rF′＝（0.1，0.1）m。

混合模型计算平台为MATLAB环境，数值模型计算平台为SYSNOISE 5.5。表1给出了由FE计算得到的7阶板模态和7阶声腔模态。

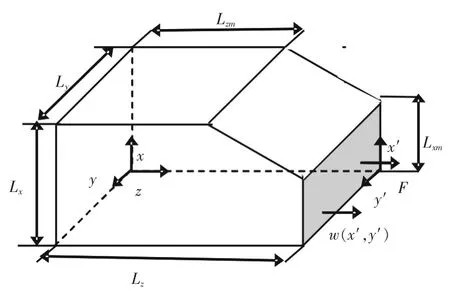
图3 板与声腔耦合模型

表1 平板和声腔的固有频率

为了比较耦合FEM－WBM的性能，构造了4个模型。混合模型1采用50个FE单元；混合模型2为100个；混合模型3为200个；作为参考模型的数值计算模型则采用625个板有限单元和4 151个边界单元。

图4和图5为板法向位移变形图和声腔内y′＝0.25 m平面的声压分布，图4可以看出系统的响应由非耦合结构模态控制。

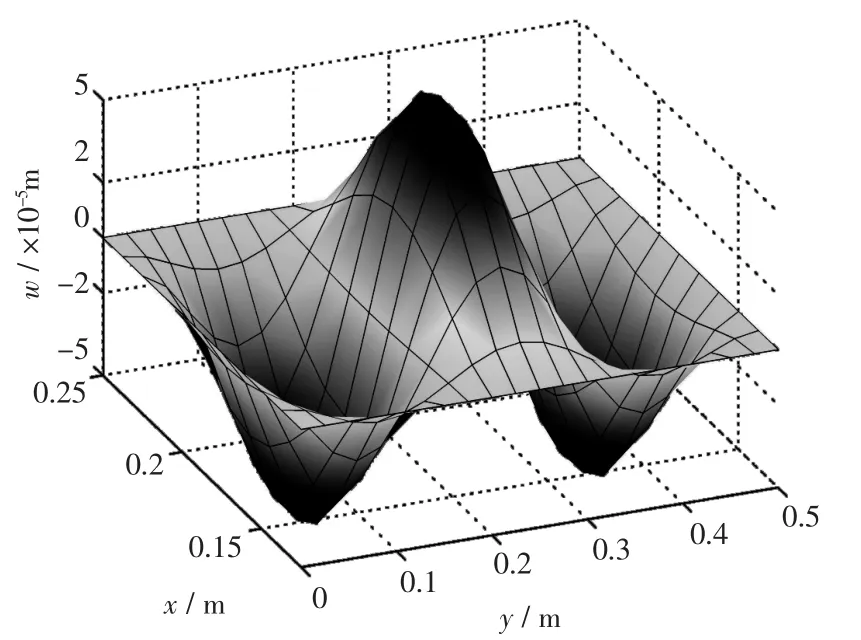
图4 336 Hz时板法向位移

图6为板（0.2 m，0.2 m）处的位移响应和声腔（0.25 m，0.25 m，0.375 m）处的声压响应。从响应谱可以看出对于3种混合模型低频段 （1～250Hz）吻合较好。

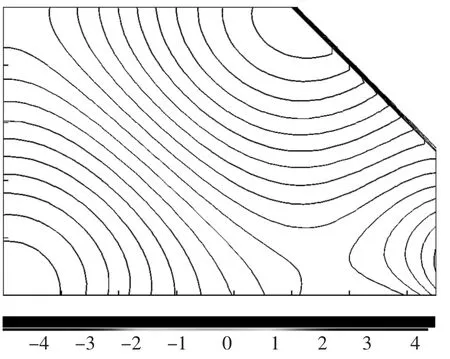
图5 声压分布/Pa

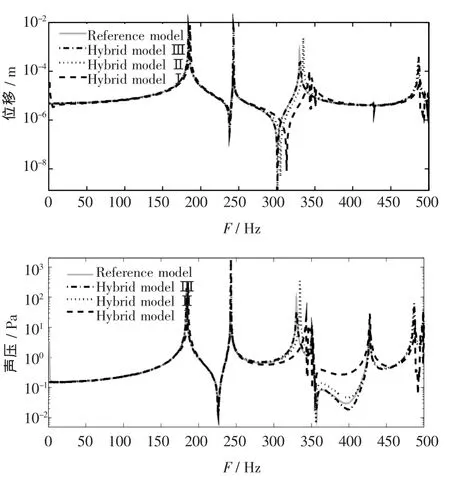
图6 板的位移响应和声腔的声压响应

在高频段 （250～500 Hz），除了混合模型3外，其他2个模型与参考值有较大偏离。这主要是因为混合模型中FE部分的数值误差。

从图6还可以得出：耦合模型的计算精度基本上取决于FE模型的精度，也与FE频率响应函数特性相似，都是向高频偏移。所以利用FE随网格细分而精度提高的特点进一步细分网格，那么一定能得到精度非常满意的计算结果。而传统的模态叠加法一般适合低频的分析，随着频率的增加越来越多的模态对系统的整个响应都有贡献，此时模态叠加法变得不适合。文中方法将声腔的声压用满足赫姆霍兹控制方程的波函数展开，用于分析声腔部分的自由度大大减少，最后耦合模型的总自由度数仍少于耦合有限元和边界元法，这有利于计算更高频率或者更高精度的耦合问题，从图7可以发现这点。

6 结束语

本文讨论了分析三维结构声系统动力学响应的混合方法。WBM具有计算模型小，收敛速度快，计算量比FEM少等特点，与FEM相比该方法提供了处理更高频率响应的能力。但是为了利用WBM的计算效率，分析模型只能是中度复杂的几何模型。一个充分非必要条件是求解域必须是凸形域。对于非凸形域需要将其分解成多个子域，在界面施加连续性条件。对于实际的问题，WBM可能需要大量的子域。为了处理更加复杂的几何模型，提出了混合FEM－WBM。混合法利用了WBM的高计算效率以及FEM的几何适应能力。

图7 336 Hz时收敛曲线

两种方法的近似场通过加权余量公式来直接耦合。混合法的性能通过一个简单的耦合模型来验证。由结果分析也说明了混合法的特点。由于混合法中存在FE部分，所以混合法也存在数值误差。利用FEM的细分，可以得到更高精度的结果。该方法可以为有源结构声控制提供一定的理论基础。

将来的工作将对WBM的耦合方程的高效、稳定算法方面进行深入研究。研究耦合WBM和BEM的可能性，以及探索流固耦合界面上存在阻尼材料的情况。

［1］ RAO Z S，LUO C，ZHAO M.The analysis of structuralacoustic coupling of an irregular enclosure under the excitation of point force and PVDF［J］.Journal of Vibration and Acoustic，2007，129：202－208.

［2］ LUO C，RAO Z，ZHAO M.The Analysis of Responses of an Irregular Enclosure Excited by a Pair of PVDF Piezoelectric Film［J］.Journal of Vibration Engineering，2004，17（22），895－897.

［3］ LI Y Y，CHENG L.Vibro－acoustic analysis of a rectangular－like cavity with a tilted wall［J］.Applied Acoustics，2007，68（7）：739－751.

［4］ JUNGER M，FEIT D.Sound，structures and their interaction［M］.Cambridge：The MIT Press，1986.

［5］ DOWELL E H，VOSS H M.The effect of a cavity on pan-el vibration［J］.AIAA Journal，1963，1：476－482.

［6］ ZHANG Q J，SAINSBURY M G.The Energy Flow Method for strongly coupled systems［C］//Proceedings of the 17th International Modal Analysis Conference，Kissimee，Florida，USA，1999：1839－1845.

［7］ DOWELL E H，GORMAN G F，SMITH D A.Acoustoelasticity：general theory，acoustic natural modes and forced response to sinusoidal excitation，including comparisons with experiment［J］.Journal of Sound and Vibration，1977，52（4）：519－542.

［8］ LUO C，ZHAO M，RAO Z S.The analysis of structuralacoustic coupling of an enclosure using Green＇s function method［J］.The International Journal of Advanced Manufacturing Technology，2005，27（3/4）：242－247.

［9］ WU J H，CHEN H L，HU X L.Method to calculate interior sound field of arbitrary-shaped closed thin shell［J］.Acta Acustica，2000，25：468－471.

［10］ ZHANG S，CHEN N.New analytical method for modeling active structure acoustic control system within an irregular enclosure［J］.Journal of Low Frequency Noise，Vibration and Active Control，2005，24（4）：265-273.

［11］ DESMET W.A wave based prediction technique for coupled vibro－acoustic analysis ［D］.Katholieke University Leunen，1998.

［12］ VAN HAL B.Automation and performance optimization of the wave based method for interior structural－acoustic problems［D］.Katholieke University Leunen，2004.

［13］ HUANG F，HE Z，PENG W C.An efficient prediction method for the two－dimensional coupled structural－acoustic analysis［J］.Acta Mechanica Solida Sinica，2006，19（4）：327－333.

［14］ PENG W C，HE Z，LI P，WANG J Q.A prediction technique for dynamic analysis of flat plates in the mid－frequency range［J］.Acta Mechanica Solida Sinica，2007，20（4）：333－341.

［15］ PENG W C，HE Z，WANG J Q.Application of domain decomposition in acoustic and structural acoustic analysis［J］.Chinese Journal of Mechanical Engineering，2007，20（6）：87－93.

［16］ 彭伟才，何锃，李鹏.耦合FE／WB法在声分析中的应用［J］.计算物理，2009，26（3）：396－402.

A Hybrid Method for Interior Structural－acoustic Analysis

Peng Wei－caiZhao Gao－yu He Zeng
Department of Mechanics，Huazhong University of Science＆Technology，Wuhan 430074，China

The finite element method（FEM）is a widely accepted prediction tool for the steady－state dynamic response analysis of coupled structural－acoustic（SA）systems.However，it is limited to the low frequency range due to the fast growing model size for increasing frequencies.An alternative method is the wave based method（WBM）based on the indirect Trefftz method.However，the applicability of the WBM is limited since the high computational efficiency only appears for moderate geometrical complexity.In order to take advantage of the wide application range of the FEM and the high convergence rate of the WBM，a hybrid method of the two is proposed.The basic idea is to replace parts of the FE model with simple geometrical shapes by much smaller wave models.The resulting hybrid model has fewer degrees of freedom.The theoretical background of both the FEM and the WBM is briefly discussed，followed by the mathematical description of the hybrid FE－WB method.The hybrid modeling concept is demonstrated for a structural－acoustic system.The results are shown to be in good agreement with numerical simulation results.The example illustrates that the hybrid FE－WB method has the potential to cover the mid－frequency range.

structural-acoustic analysis；direct coupling；hybrid method；WBM；FEM

O42

A

1673－3185（2009）05－14－06

2009－06－05

国家自然科学基金资助项目（10872075）

彭伟才（1981－），男，博士研究生。研究方向：结构振动与噪声控制。E-mail：pweicai＠gmail.com