关于切线长定理应用的教学反思

赵玲智

中学课本的切线长定理的内容是： 从圆外一点引圆的两条切线，它们的切线长相等，并且这点和圆心的连线平分两条切线的夹角。基本图形是：

它的应用形式：

∵PA、PB分别切圆O于A、B

∴PA=PB ∠BPO=∠APO

在初中数学教材上，这是一个综合性比较强的图形，它贯穿了很多的初中几何知识点 ，包括

① 等腰三角形的性质

∵PA=PB ∠BPO=∠APO

∴BE=AEOP⊥AB

这其实就是等腰三角形“三线合一”

②三对全等三角形 Rt△OBP≌Rt△OAP,

Rt△OBE≌Rt△OAE Rt△EBP≌Rt△EAP

利用切线长定理或三角形全等可以得：

∠BOP=∠AOP ∠EBP=∠EAP∠OBP=∠OAP

以及线段BE=BAOA=OB PA=PB

③实际上这六个直角三角形连起来相似

Rt△OBP∽Rt△OAP∽ Rt△OBE∽Rt△OAE∽Rt△EBP∽Rt△EAP

④有射影定理的基本图形，所以又出现了一些相等关系的等式OB²=OE•OP =OA EB²=OE•EP= EB²

⑤有OP⊥AB以及切线的性质OA⊥AP,OB⊥BP这就引出了更重要的知识点:三个垂直关系

OA⊥AP,OB⊥BP，OP⊥AB

可以列出图形的面积关系。

即SAPBO=OA•AP=OB•BP=OP•AB

⑥在圆O中有OP⊥AB这就引出了圆中更重要的定理出现了垂径定理

∵在圆O中OP⊥AB

∴NB=NABM=MA

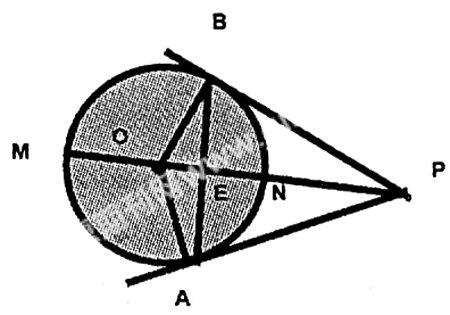
⑦事实上利用切线的性质OA⊥AP,OB⊥BP可以得到四边形OAPB四点共圆

⑧如果在圆周上任意取一点Q（或Q′） 有可以把圆中的圆心角、圆周角定理联系起来，这样图中∠APB、∠OPA、∠OPB、∠Q、∠AOB、∠BOA、∠OBA、∠OAB、∠EBP、可以已知其一可求其他

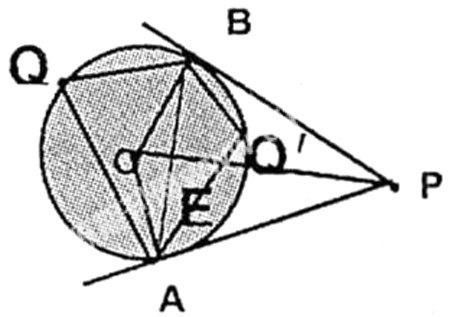
⑨当然过AB任意点做切线后图中又出现两组切线长MB=MT,NT=NA，于是有△PMN的周长=PA+PB=2PA

初中数学教材上还有一些综合性很强的典型题，这里只是浅浅的一想，供大家参考，还希望各位同仁给以批评指正。