浅谈数形结合的记忆功能
2009-02-07董艳华
董艳华
摘要数形结合是抽象的“数”与直观的“形”的完美统一。数学中众多抽象的概念、公式、定理等,既可以有“形”的本质又可以赋予“形”的描述,这种抽象与直观的变换使数形结合思想具有独特的记忆功能。教学中,笔者沿着数形结合思想的轨迹找到一些记忆的有效途径:以形释数理解记忆,实验演示影像记忆,勾勒情景想象记忆。
关键词数形结合 记忆 直观图形
随着时代的发展,教育改革的不断推进,数学思想方法教学越来越受广大教育者重视,其中数形结合思想以其化抽象为直观的良好特性而倍受教师们的青睐。在数学教学中,数形结合思想具有提高学生的学习兴趣,拓展学生的解题途径,发展学生的思维能力,促进学生的有效记忆等多种教育功能。数形结合思想的记忆功能主要是用图象帮助记忆。我们经常说,一幅图胜过一千个字。实验研究表明,图像记忆的效率至少是声音记忆的100倍以上,是一种记得快而忘得慢的“过目不忘”的记忆方式,能大大提高我们的记忆效率、学习效率。笔者根据多年数学教学经验总结出以下几种方式实现数形结合的记忆功能。
一、以形释数,理解记忆
可尔莫哥洛夫提出“对于抽象的东西,能够在头脑中像画画一样描绘出来并加以思考”的几何直观。很多抽象的数学知识都有一定的几何意义,我们可以通过其几何图形表示化抽象为直观,以直观图形的方式促进学生的理解和记忆。
(一)用图形解释记忆概念
直观图形在传递概念时,给人的信息是完整的;显示结构时,可以用表象信息来贮存语言信息,而借助于表象更容易形成长时记忆。我们就利用这种数与形的结合,为概念赋予图形信息,利用图形信息来帮助学生理解记忆概念。
例如,概率中的四个基本概念,事件A和事件B的积事件、事件A和事件B的和事件、互斥事件和对立事件,文字叙述艰涩难懂,学生难以理解,而且互斥事件和对立事件又是两个相近概念,学生容易混淆,记住这些概念就更加困难。教学时,可以用图1-图4这四个文氏图图形分别表示它们:
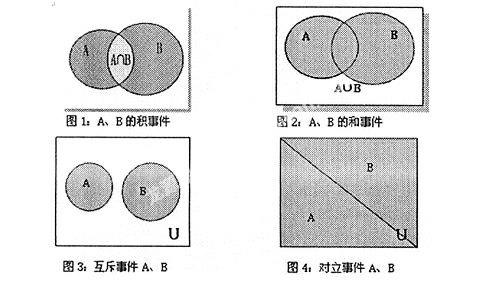
由图形可知,事件A和事件B的积事件就是两个事件集合的公共部分;事件A和事件B的和事件就是两个事件集合的全部;互斥事件就是两个不能同时发生的事件;对立事件就是两个事件中有且仅有一个发生的事件;是对立事件必定为互斥事件,但互斥事件不一定是对立事件。通过4个图形,几个基本概念的联系、区别一目了然。用图形来剖析概念知识,给概念附上几何意义,为记忆保持了形象支持,有效促进了概念的记忆。
(二)用图形揭示记忆公式
数学中公式繁多,记忆较麻烦,是令很多学生头疼的一件事。其中三角函数模块中公式就比较突出,如同角三角函数的基本关系式,诱导公式等等有几十个,学生花费很多力气也未必能把他们记清楚。要是抓住三角函数的几何意义,很多公式记忆问题就迎刃而解了。由三角函数的概念可知,三角函数的直观几何表示是依托于直角坐标系和单位圆的三角函数线,如图5所示:
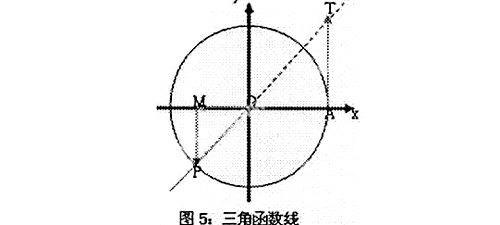
OP是角A的终边,有向线段OM是正弦线,MP是余弦线,AT是正切线,它们的长短就代表相应三角函数值的大小,它们的方向就代表了相应三角函数值的正负。根据角的终边位置及对应的三角函数线,任意一个象限角的相应三角函数值符号见图便知,并可以把各个结果总结为图6表示几种情况:
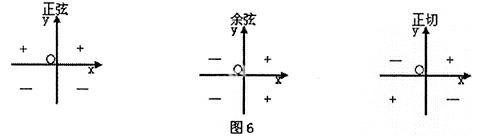
每种三角函数在各个象限的符号很快就被记忆下来。据此,结合“奇变偶不变,符号看象限”的口诀(如“sin(180°+A)=-sinA”, 180°是90°的偶数倍,函数名称不变,即公式右边仍然是A角的sin值;把A看成锐角,则180°+A是第三象限角,第三象限角的正弦值是负数,所以在公式右边的sinA前加上一个“-”,就得到了sin(180°+A)=-sinA的公式),学生就能在短时内记住三角函数的六组诱导公式而且不容易忘记。
(三)通过图形反映记忆性质
很多数学中的性质,如函数的单调性、奇偶性、最值和极值,不等式的对称性、传递性等等,都能通过图像直观反映出来并得到很好的记忆。例如,不等式的可加性,“如果a>b,那么a+c>b+c。”我们根据实数与数轴的对应关系,把c看成距离,把a和b看成数轴上的点,如图7所示:
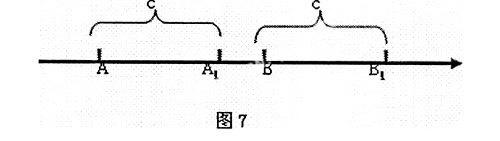
A处是a,B处是b,a由A移动到A1,b由B移动到B1,通过移动相等的距离c两数的大小都变了,但两者的大小关系不变。通过图形的直观反映,学生既知其然又知其所以然,理解记忆得更加深刻了。
(四)通过图形表示记忆运算
数学中的很多运算也可以通过图形表示并加强记忆。向量的加法运算和减法运算是典型的数形结合,它们的整个运算过程用文字几乎难以描述,但是都可以通过图8-图10的三个图形来完成。
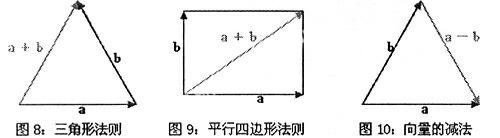
集合间的基本运算,交集、并集、补集也可以如图1、3、4一样,用几个文恩图全面形象的表示出来。有了这种直观的认识,学生便能很容易的把相关的数学运算记忆在心了。
教学时,教师要善于引导学生用数形结合思想揭示问题的本质联系,用“形”的直观启迪“数”的思维,从而使数学知识在直观理解中得到有效记忆。
二、实验演示,影像记忆
以形释数,可以将数量关系的空间形式跃然纸上。然而“纸上得来终觉浅,绝知此事要躬行。”教育家陶行知先生曾提出“生活教育”理论的核心——“教学做合一”,教师要在做中教,学生要在做中学。我们通过“做”,让数形结合动起来,使学生的记忆更加深刻。
例如,算法中实现a、b值交换的赋值语句,x=a,a=b,b=x。学生对此交换既难理解又难记住。我们可以准备三个杯子,其中一杯盛水,一杯装橙汁,一个空杯,让学生动手操作实现水与橙汁的交换。交换过程如图11所示:
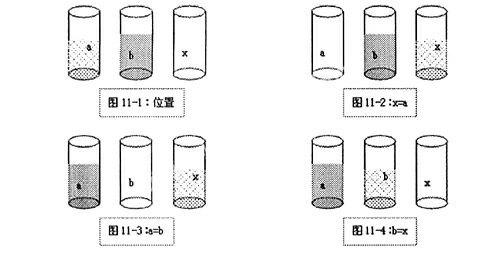
经过实验演示,a、b、x就好像一个个活生生的实物,a、b的交换过程恰是一段实物交换影像。真切的实验演示,简单的实物交换化解了数学中的复杂关系。通过实物操作的变换过程,学生理解了x的储存作用,记住了三个赋值语句的先后顺序。
美国心理学家威廉•詹姆士说:“一件在脑子里的事实,与其他事物发生联想,就很容易记住,所联想的其他事物,犹如一个个钓钩一般,能把记着的其他事物钓出来。”有了实验的影像,当你回忆时,脑海里会自发的重现当时的现象,再提及时就会更加容易的打开记忆之门。实验演示让数学插上了有形的翅膀,载学生在知识的海洋中畅游。
三、勾勒情景,想象记忆
最形像的数形结合莫过于对身边生活的贴切形容,这样就像电视、电影、小说一样,在人的头脑中产生虚拟现实的立体画面来刺激大脑,并使之产生强烈的条件反射,因而更容易为人们所把握、记忆。
我们把需要记住的事物知识串联到一起,并且在大脑中形成一连串物象来记忆,虽然这些物象并不是知识的本质解释,不反应数学本质,但因为它的情景化而很容易被感知被记住。记忆圆周率时,3.14159可以想象成“山巅一寺一壶酒”这样的情景记忆。单位换算1弧度=0.0174529度可以想象成“零点令伊妻赐吾二两酒”。尽管看起来圆周率和情景中的山上寺庙毫不相干,零点和他的妻子的生活与弧度的转化风马牛不相及,但这种记忆方式是非常有效的。日本学者保坂荣之介认为:通过形象的浮现,大脑肯定会向我们的身体发出变化的指令信号。实际上,这里面正好隐藏着记忆力注意力的秘密……增强注意力、记忆力的动力,似乎就隐藏在如何控制想象记忆中。
数形结合不是记忆灵丹妙药,但确实是一种实现记忆的有效途径。教学中我们要善于发现善于总结,让数形结合的记忆功能发挥得更好。
参考文献
[1]张海洋,如何提高记忆力,中国记忆力训练网,2006年11月。
[2]谢定兰主编,《名师—记忆效果的秘诀》,西南师范大学出版社,2008年2月第1版。
[3]曾琦主编,《(新思考)学生学习》,华东师范大学出版社,2006年9月第一版。
[4]王颖,浅系数形结合的数学教育意义,《教学与管理》2004年12月20日
