非均质土体中渗流场的非平稳随机模拟

李少龙，张家发

实际渗流场受众多随机因素的影响因而具有一定程度的不确定性。近年来，渗流场随机分析得到关注，较多的研究是在考虑渗流参数随机性的基础上将渗流场的不确定性定量化，分析随机渗流场的分布规律及结果的可靠性。文献［1］将各渗透分区的参数作为随机变量，采用一阶Taylor展开随机有限元法对地下水承压流进行随机模拟。文献［2］将裂隙系统的几何参数作为随机变量，用一阶Taylor展开随机有限元法分析了裂隙岩体渗流场的随机性。将岩土体参数作为随机变量，实际上忽略了它们的空间相关性，不符合实际情况。文献［3］将渗透系数作为平稳随机场，应用小参数摄动法得到稳定渗流的随机有限元列式，通过算例分析了水力坡降标准差与渗透系数变异性之间的关系。文献［4］将渗透系数作为平稳随机场，采用 Monte－Carlo（MC）随机有限元法，研究了土体渗透系数的随机性对有压渗流场统计特征的影响。文献［5］提出了可用于高阶分析的KLME方法，将渗透系数作为对数正态平稳场，通过有压渗流的算例与MC方法进行比较，分析表明该方法具有较高的计算精度和效率。

土性参数具有随机性和空间相关性，用随机场描述这种空间变异性是比较合适的，很多随机渗流分析已经引入了二阶平稳随机场，然而一些情况下二阶平稳随机场仍不足以描述参数的空间分布特征，如当渗透系数的空间分布呈趋势性变化时，不满足平稳场的均值为常量的要求，此时需要考虑非平稳的随机渗流分析。文献［6］采用一阶非平稳谱方法研究了渗透系数具有趋势性变化时渗流场的统计特征，为了便于推导解析解而没有考虑边界的影响，并假定趋势变化的方向与流动方向一致。文献［7］用一阶矩方程法分析了对数渗透系数场的均值函数呈线性、二次和周期性趋势变化时水头方差的异同。本文将渗透系数作为非平稳随机场，考虑均值函数的连续型和间断型两种空间趋势变化，应用KLME方法计算水头统计矩的二阶结果，探讨参数场的非平稳性对渗流场统计特征的影响。

1 渗透系数随机场

土体渗透系数在空间上的变化，既具有随机性又具有结构性，对这种空间变异的一种处理方式就是用随机场进行描述，如文献［8］提出土性剖面的随机场模型，考虑了土性空间变异的两重性，在岩土工程中得到较大应用。

应用随机理论分析问题时通常会引入一些假定，较常用的一个假定就是将参数随机场作为二阶平稳场，即：均值在空间上为常数；协方差函数仅依赖于空间两点之间的相对距离。Vanmarcke等人提出的模型实质上是用高斯平稳随机场模拟土性剖面。文献［9］对获取的土层静力触探试验资料进行平稳性检验，发现锥尖阻力和侧摩阻力两组数据均有明显的随深度变化的趋势，去除趋势项后的数据满足二阶平稳性。试验数据并不总是满足二阶平稳条件，一般来讲，土性会随着空间位置呈趋势性变化，土工试验中发现比贯入阻力［10］、不排水抗剪强度［11］等随土层深度变化，通常可用线性函数来近似表示。在一些研究中发现渗透系数也具有空间趋势性变化，文献［12］报道了在美国密西西比州东北部城市哥伦布的一个试验研究揭示渗透系数存在空间分布上的趋势变化。

一般地，可将随机场分解表示为

式中：f（x）为土性随机场；μ（x）为随机场的均值函数，在地质统计学中亦称为漂移，通常作为确定性的函数；ε（x）是零均值的空间随机函数，它是随机场围绕均值的局部小扰动分量；x为空间点。为了探讨渗透系数的趋势变化对渗流场统计特征的影响，本文考虑均值函数的连续型和间断型2种趋势性变化。连续型趋势采用线性函数表示：

式中：x1和x2为二维空间中2个方向上的坐标；a0为均值的初始值；a1和a2为线性分布系数即斜率。间断型趋势采用分段函数表示：

式中：D1和DN分别为第1类和第N类土所在的空间区域；μ1和μN分别为第1类和第N类土的渗透参数均值。这种处理类似于确定性模型中对渗透系数进行分区。本文的这2种处理可认为是近似概括，对于实际问题需根据实测数据具体分析。经以上处理后，可认为随机场扰动项ε（x）是二阶平稳的。

根据大量的工程实测资料，一般渗透系数呈对数正态分布［2］，文献［13］收集的试验研究结果亦表明可认为渗透系数服从对数正态分布。本文亦采用该分布，这样对数渗透系数 f（x）＝ln（x）就是正态随机场。为了使用数值方法求解随机渗流问题，需要将参数随机场离散化，本文采用抽象离散即随机场的 Karhunen－Loeve展开［5，14］：

式中：χi为随机场协方差函数的特征值；Ψi（x）为与特征值相对应的特征函数；ξi为随机变量。

2 随机渗流模型

下面根据渗流基本原理建立稳定渗流随机模型，

式中：H（x）为水头；K（x）为渗透系数；Hd（x）为Dirichlet边界ΓD上的已知水头；n（x）为边界上的单位外法线向量；q（x）为Neumann边界ΓN上的已知流量。由于将渗透系数作为随机场，所以水头也是具有一定概率分布的随机函数。

将水头展开为摄动级数

式中：H（0）为确定性的零阶展开项；其余依次为一阶、二阶和三阶展开项。结合参数场的 KL展开（4），可将各阶水头表示成如下多项式

本文考虑水头的三阶展开。只要求得展开式中的各阶系数 H（0），H（1），H（2），H（ij3k）等，就可得到水头的随机表达式。将式（4）、（6）、（7）代入方程（5），并结合随机微分方程的扰动展开，可以得到关于水头展开系数的确定性偏微分方程组

式中：m为方程阶数；Kg（x）＝eμ（x）为渗透系数的几何均值。传统的随机方法通常忽略二阶及以上高阶项，只求解水头的一阶均值和方差。本文应用KLME方法可求得水头的二阶均值和方差式（9）和（10）等号右端第一项分别为一阶水头均值和方差。方差的平方根即为标准差。本文将二阶均值或标准差与一阶均值或标准差之差分别称为水头均值和标准差的二阶修正，记为Δ〈H〉和ΔσH。

3 算例分析

为了简化分析，取10 m×10 m的矩形域为研究区。左右两侧为定水头边界，总水头分别为15 m和10 m，上下侧边为零流量边界。

算例1分析连续型趋势下渗流场的统计特征，对数渗透系数场的均值系数a0＝0，方差σ2f＝1，即渗透系数的几何均值为1 m／d，变异系数为131%。协方差函数采用离散指数型［5，14］，相关尺度 λ＝1 m。考虑5种计算方案，计算参数如表1所示，其中方案1不考虑参数场的趋势变化，其余4个方案分别考虑2个方向上的线性递增或递减。表中参数对应渗透系数的几何均值变化范围为0．223～4．482 m／d。

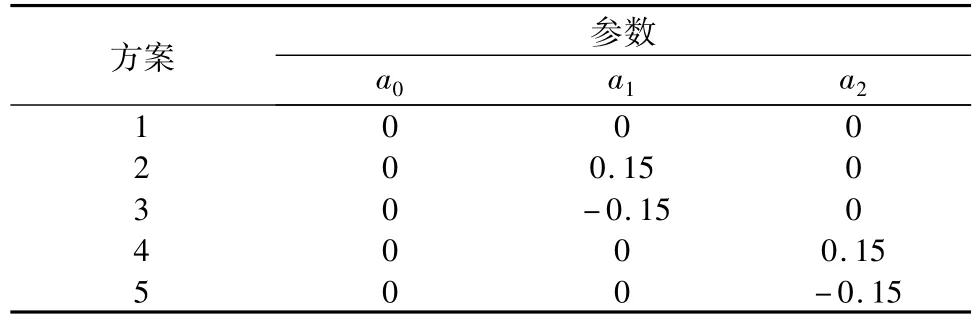
表1 算例1的计算参数Table 1 Calculation parameters in example one

在给定的几何条件和边界条件下，当 μ（x）在空间上为常数，即在无趋势变化时，平均水头在x1方向是线性分布，如图1所示；在x2方向上平均水头是常量。图2为水头标准差 σH的等值线图，由图可见σH在研究域上对称分布，并在研究域中部形成峰值带。沿x1方向，σH在左右边界上由于水头为常量这一确定性边界条件的限制所以为零，向区域中心不断增大。沿x2方向，水头标准差在区域中心最小，向两侧的无流量边界递增。两侧边界上的流量虽然是确定性的，然而水头仍是随机变化，因而水头标准差并不为零。

图1 x1方向上的水头均值Fig．1 Mean head along x1 axis

图2 计算方案1的水头标准差Fig．2 Standard deviation of head for case 1

对于方案2，μ（x）在x1方向上线性增加，水头均值〈H〉不再是线性分布，比方案1在数值上要小，见图1。由于左部渗透系数低，右部渗透系数较大，相对而言左部对流动有阻碍作用，而在给定的条件下水流必须是从左到右渗透，因而水头在左部降低较显著，渗透坡降J较大。由图3可见，水头标准差σH的峰值带移向区域的左部。基于一阶谱分析的解析解［13］表明 ，σ2H＝cσ2fJ2λ，式中：c为系数，随问题的空间维数而不同。本计算方案中σH峰值带出现在较大渗透坡降J的空间域，与解析解的结果一致。在x2方向上，σH关于区域中心对称分布。比较图2和图3显见，渗透参数场的趋势变化影响了水头统计矩的空间分布。

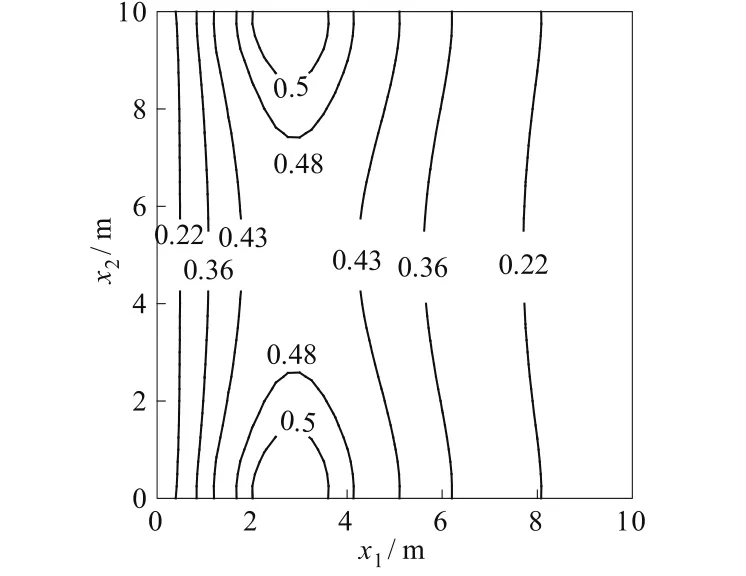
图3 计算方案2的水头标准差Fig．3 Standard deviation of head for case 2

方案3与方案2相反，μ（x）在 x1方向上线性减小，〈H〉也不是线性分布，比算例1在数值上要大。由图1可见，水头在区域左部增大，因为左部渗透系数大流动阻力小；而右部渗透系数小流动阻力大，水头下降较大。如图4所示，σH的峰值带偏向于研究域的右部。在x2方向上，σH仍是关于区域中心对称分布。

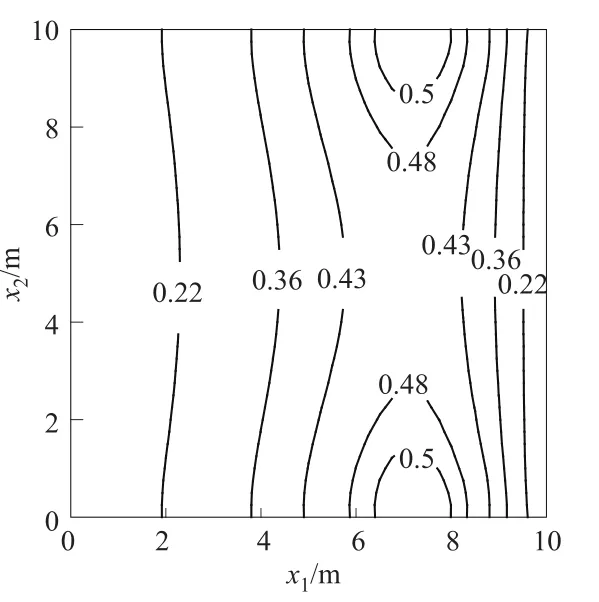
图4 计算方案3的水头标准差Fig．4 Standard deviation of head for case 3

图5 计算方案4的水头标准差Fig．5 Standard deviation of head for case 4

对于方案 4，μ（x）在垂直于平均水流方向的x2方向上线性增加。在给定的边界条件下垂直于平均流动方向的线性趋势不影响平均水头，水头均值与算例1的分布一致，然而 x2方向上的 σH不是对称分布，σH的峰值偏向区域中渗透系数较大的一侧，如图5所示。若将流动域视为由多个土层组成流动方向平行于各土层，这时渗流主要集中在渗透系数较大的土层中，σH也在该区域集中而且具有较大数值。方案5的水头标准差分布与方案4相反，不再赘述。

图6 不同斜率a1时水头均值的二阶修正Fig．6 2nd order correction of mean head for different a1

图7 不同系数a1时水头标准差的二阶修正Fig．7 2nd order correction of standard deviation of head for different a1

在计算方案2的基础上增大斜率a1为0．3并和方案1进行比较，以考察水头统计矩高阶项在不同程度趋势变化中的作用。图6和图7为研究域的x1方向中心线（x2＝5 m）上水头均值和标准差的二阶修正的分布图。由图可见，当参数场无趋势变化时，水头均值和标准差的二阶修正的数值较小，随着斜率a1的增大，二阶修正的峰值也不断增大。由此可见，当渗透系数具有较强的空间趋势变化时，水头统计矩高阶项的作用变大，此时传统的一阶Taylor或摄动方法不能满足要求，需要求解高阶项的方程。

图8 间断型趋势条件下水头均值Fig．8 Mean head for discontinuous trending example

算例2考虑间断型趋势，研究域内共有3类土，其中的一类土 μ1＝0，另两类土位于该类土之中，μ2＝－1，D2＝｛2≤x1≤4，4≤x2≤7｝；μ3＝1，D2＝｛6≤x1≤8，2≤x2≤6｝，图8和9中的虚线框即表示它们所在的位置。本算例与算例1中方案1的参数不同在于嵌入两渗透系数几何均 值 分 别 为 0．37 m／d和7．4 m／d的土块，然而水头均值呈现出明显的非均匀分布。比较图2和图9可见，两者的水头标准差的空间分布相差较大，在参数场的间断型趋势条件下，σH不再是对称分布，σH在渗透系数较小的区域内及周围增大，而在渗透系数较大的区域内σH的分布较均匀。若这两种介质出现在研究域内其它位置，水头均值和标准差同样会呈现非规则的分布。

图9 间断型趋势条件下水头标准差Fig．9 Standard deviation of head for discontinuous trending example

4 结 语

本文将渗透系数作为对数正态非平稳随机场，分解为确定性趋势和平稳性波动，运用KLME随机数值方法，讨论了参数场的连续型线性趋势和间断型趋势分布对渗流场统计特征的影响。相对于无趋势情况，参数场的趋势性分布改变了水头统计矩的空间分布形态，其分布受到线性趋势性变化方向的影响，随着线性趋势的斜率增大，水头均值和标准差的二阶修正项的作用也增大，在参数场间断型趋势条件下，水头统计矩呈现复杂的非规则空间分布。因此，在土性参数的统计分析时应注意识别参数是否具有非平稳性。本文仅考虑了随机场的均值函数在空间上有趋势变化，实际工程中地层包含多个土层，不同土性的统计参数如方差、相关尺度等可能不同，那么随机场的非平稳性还将体现在协方差函数在空间上变化，这时渗流场的随机模拟更复杂，有待进一步研究。

［1］ 姚磊华．地下水水流模型的Taylor展开随机有限元法［J］．煤炭学报，1996，21（6）：566－570．

［2］ 盛金昌，速宝玉，魏保义．基于Taylor展开随机有限元法的裂隙岩体随机渗流分析［J］．岩土工程学报，2001，23（4）：485－488．

［3］ 李锦辉，王 媛，胡 强．三维稳定渗流的随机变分原理及有限元法［J］．工程力学，2006，23（6）：21－24．

［4］ GRIFFITHSD V，FENTON GA．Seepage Beneath Water Retaining Structures Founded on Spatially Random Soil［J］．Geotechnique，1993，43（4）：577－587．

［5］ ZHANGD，LU Z．An Efficient，Higher－order Perturba－tion Approach for Flow in Randomly Heterogeneous Por－ous Media Via Karhunen－Loeve Decomposition［J］．J Comput Phys，2004，194（2）：773－794．

［6］ LI S G，MCLAUGHLIN D．Using the Nonstationary Spectral Method to Analyze Flow Through Heterogeneous Trending Media［J］．Water Resour．Res．，1995，31（3）：541－551．

［7］ ZHANG D．Numerical Solutions to Statistical Moment E－quations of Groundwater Flow in Nonstationary Bounded Heterogeneous Media［J］．Water Resources Research，1998，34（3）：529－538．

［8］ VANMARCKE E H．Random Fields：Analysis and Syn－thesis［M］．Cambridge，Massachusetts：The MIT Press，1984．

［9］ 闫澍旺，贾晓黎，郭怀志，等．土性剖面随机场模型的平稳性和各态历经性验证［J］．岩土工程学报，1995，17（3）：1－9．

［10］李镜培，高大钊．桩基承载力参数估计的随机场模型［J］．岩土工程师，1992，4（2）：1－6．

［11］冷伍明，赵善锐．土工参数不确定性的计算分析［J］．岩土工程学报，1995，17（2）：68－74．

［12］REHFELDT K R，BOGGS J M，GELHAR L W．Field Study of Dispersion in A Heterogeneous Aquifer，3，Geostatistical Analysis of Hydraulic Conductivity［J］．Water Resour．Res．，1992，28（12）：3309－3324．

［13］杨金忠，蔡树英，黄冠华，等．多孔介质中水分及溶质运移的随机理论［M］．北京：科学出版社，2000．

［14］YANG J，ZHANG D，LU Z．Stochastic Analysis of Satu－rated－Unsaturated Flow in Heterogeneous Media by Com－bining Karhunen－Loeve Expansion and Perturbation Meth－od［J］．JHydrol，2004，294（1）：18－38．