高混凝土坝水荷载引起的位移分量研究
2009-01-29黄耀英沈振中周宜红
黄耀英,沈振中,田 斌,周宜红
在水荷载作用下,混凝土大坝任一监测点产生的水平位移由 3部分组成[1,2]:即水压力作用在坝体上产生的内力使坝体变形而引起的位移;在建基面上产生的内力使地基变形而引起的位移;库水荷载作用使库盘变形所引起的位移。当假设地基不透水时,上游库水荷载作为面荷载作用在地基表面,这种水荷载施加方式目前工程上仍在采用[1~3]。由于实际地基是透水性材料,大坝建成蓄水一段时间后,在地基内将形成渗流场,上游库水对地基变形的影响应按渗流体积力进行分析[4~10]。张有天[9]、王媛[10]等认为混凝土坝虽然透水,但因其渗透系数很小,水力梯度非常大,通常近似按不透水介质处理,此时坝体上游面作用水压力(面荷载),坝基面作用扬压力(面荷载),而作用在地基上的水荷载一般按渗流体荷载考虑。笔者采用同一均质各向同性地基有限元模型,基于等效连续介质模型,对比分析了作用在地基上的水荷载作为面荷载和作为渗流体荷载(或称渗流体积力)引起的地基变形,得到结论:作用在地基上的水荷载作为面荷载和作为渗流体荷载 时存在等效关系,即中L为流线路径,但该水荷载分别作为面荷载和渗流体荷载引起的地基变形差异很大。即作用在地基上的水荷载总的作用力等效,但并不一定引起相近的效应量(位移、应力等)。
由于大坝和岩基工作条件复杂,荷载、计算参数等难以准确给定。目前,工程上常采用原型监测资料反分析大坝和岩基的实际运行状态[1,11]。当采用大坝安全监控中的混合模型[1]的调整系数反演坝体混凝土弹性模量及岩基变形模量时,反演的精度与水荷载施加的合理与否有较大的关系。另外,基于实测位移分离出的水压分量,联合大坝有限元正分析,采用优化反分析方法进行参数反演时,同样存在水荷载施加的合理与否的问题。据此,对高混凝土坝上作用的不同水荷载以及水荷载的不同作用方式对位移分量的影响进行研究。
1 基本原理
1.1 渗流场分析理论
对于多孔介质材料,忽略毛细现象、非饱和部分和蒸发的影响,稳定渗流场的控制微分方程为
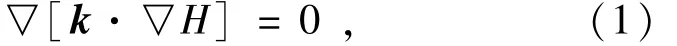
式中:为Hamilton算子;k为渗透张量;H为水头函数,H=p/γ+z,p为渗流场压力分布函数,γ为水的重度,z为铅直坐标。
其边界条件常见有如下几类:
(1)第一类边界:即 Dirichlet条件为 H|Γ1=H(x,y,z),该边界(Γ1)的水头已知;
(3)自由面及溢出面边界:
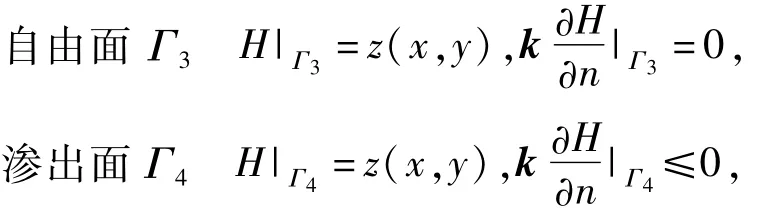
式中:q(x,y,z)为流量强度;n为外法线方向。
1.2 渗流力分析理论
设通过上述渗流分析已得到结点各点的水头值,则单元水头函数H(x,y,z)便已知。此时单元内任意点的渗透压力为
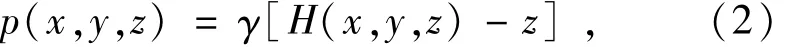
可得到单元单位体积的渗流体积力fx,fy和fz为
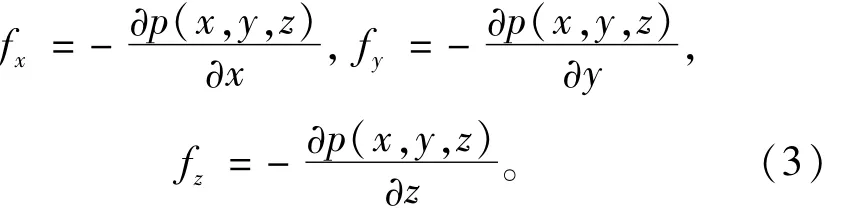
将式(3)代入式(2),并对单元体积进行积分可以得到单元总渗流体积力Px,Py和Pz为
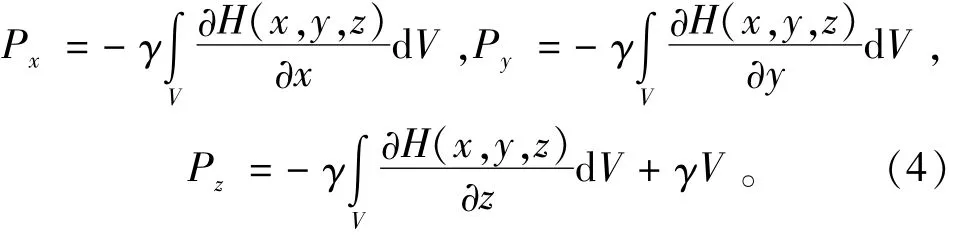
式中:V为单元的体积;γV为单元的浮力项。本文在进行渗流力分析时不计浮力项。
2 算例分析
设均质各向同性地基上坝高100 m的混凝土重力坝,上游水深90 m,下游无水,地基沿y向厚度取10 m,不考虑防渗帷幕和排水。混凝土弹性模量为20 GPa,泊松比为0.2;地基变形模量为18 GPa,泊松比为0.25。先基于等效连续介质模型计算地基的稳定渗流场,然后计算水荷载作用下大坝和地基的变形。计算地基稳定渗流场时,上下游侧面、底部和坝基面为不透水边界;计算大坝变形时,上下游施加x向连杆约束,左右侧面施加y向连杆约束,地基底部为完全位移约束。分别计算了如下几种水荷载引起的位移分量:(1)坝体上游表面的水压力(面荷载);(2)坝基面作用扬压力(面荷载),扬压力大小为渗流场计算的坝基面水头;(3)上游库水荷载分别按面荷载作用在地基表面或按渗流体荷载作用在地基内部。
2.1 工况设计
为便于对比分析,进行了如下方案的计算。
(1)地基截取范围分别为1h/1h/2h(即向上游取1倍坝高、向下游取1倍坝高、向地基深度取2倍坝高)、1h/1h/4h、2h/2h/2h、2h/2h/4h、5h/5h/2h、5h/5h/4h、5h/5h/6h、10h/10h/2h、10h/10h/6h、10h/10h/8h、40h/40h/20h、40h/40h/40h。
(2)当地基底部为刚性支承约束时,计算不同水荷载作用下大坝的位移。
(3)地基变形模量变化为30 GPa、40 GPa时,计算不同水荷载作用下大坝的位移。
2.2 计算结果及分析
分别计算了4种作用力下的位移(如图1所示)。①水压力作用在坝体上产生的内力使坝体变形而引起的位移,记为u1,该位移不随地基截取范围、边界条件、地基变形模量等变化,计算的坝顶水平位移u1=12.380 mm;②在建基面上产生的内力使地基变形而引起的位移,记为u2;③库水荷载作用使库盘变形所引起的位移,记为u3;④坝基面扬压力引起坝体的位移,记为u4。不同工况下大坝坝顶及基点(坝踵正下方1倍坝高处的岩基内)的水平位移见表1~5。表中水平位移以向下游为正,向上游为负。

图1 位移分量示意图Fig.1 Displacemen sketch
由表1~表5中数据可分析得到以下结果:
(1)由表1和表4中的数据可见,由于在建基面上产生的内力以及作用在坝基面的扬压力为有限宽荷载,当地基截取的范围足够大时,无论地基底部施加完全位移约束还是刚性支承约束,该约束条件对坝体的位移影响很小。例如地基变形模量18 GPa,当地基截取范围2h/2h/4h,底部完全位移约束时计算的坝顶水平位移u2为9.720 mm,底部刚性支承约束时计算的坝顶水平位移u2为9.820 mm;当地基截取范围10h/10h/8h,底部完全位移约束时计算的坝顶水平位移u2为11.300 mm,底部刚性支承约束时计算的坝顶水平位移u2为11.300 mm,两者相差仅为1.580 mm和1.480 mm。
(2)由表2和表3中的数据可见,作用在地基上的水荷载分别作为面荷载和渗流体荷载,其引起坝体的位移差别很大。例如地基变形模量18 GPa,底部完全位移约束,当地基截取范围10h/10h/8h,作用在地基上的水荷载作为面荷载计算的坝顶水平位移u3为-13.500 mm,作用在地基上的水荷载作为渗流体荷载计算的坝顶水平位移u3为6.102 mm,两者相差为 -19.602 mm。
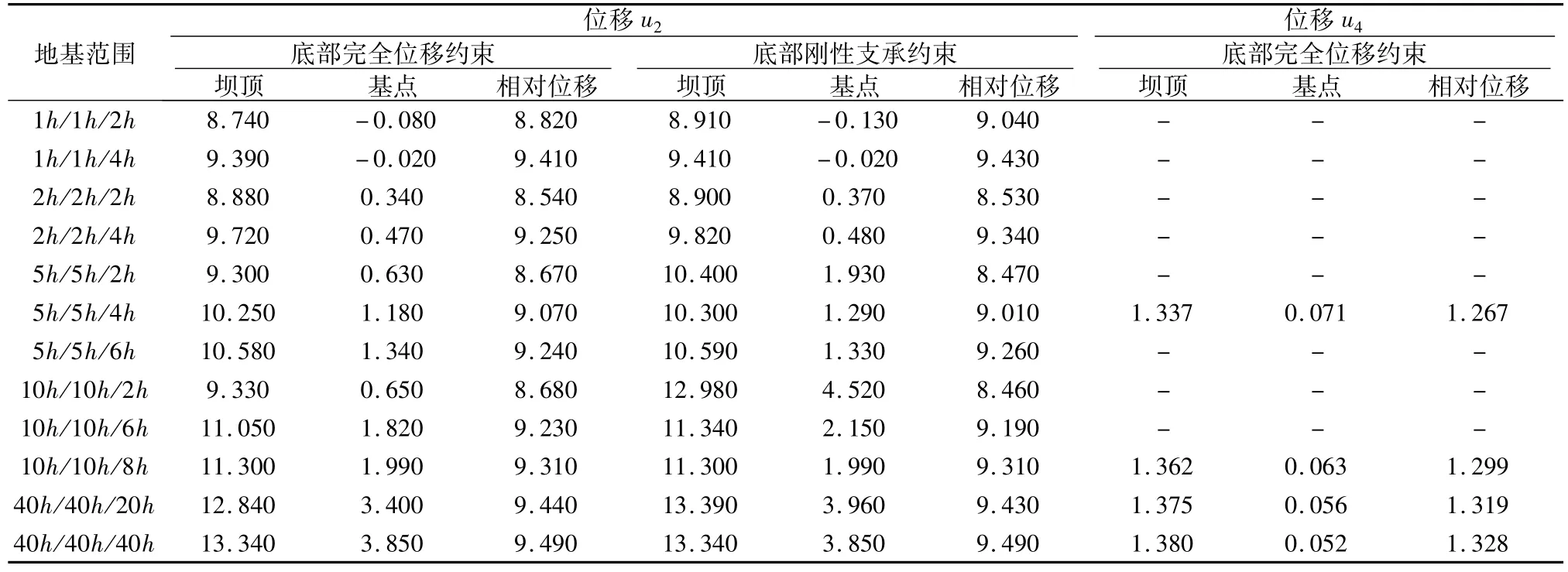
表1 地基变形模量18 GPa时不同工况下坝体水平位移Table 1 Dam's horizontal displacements under different load cases with foundation's deformation modulus 18 GPa mm
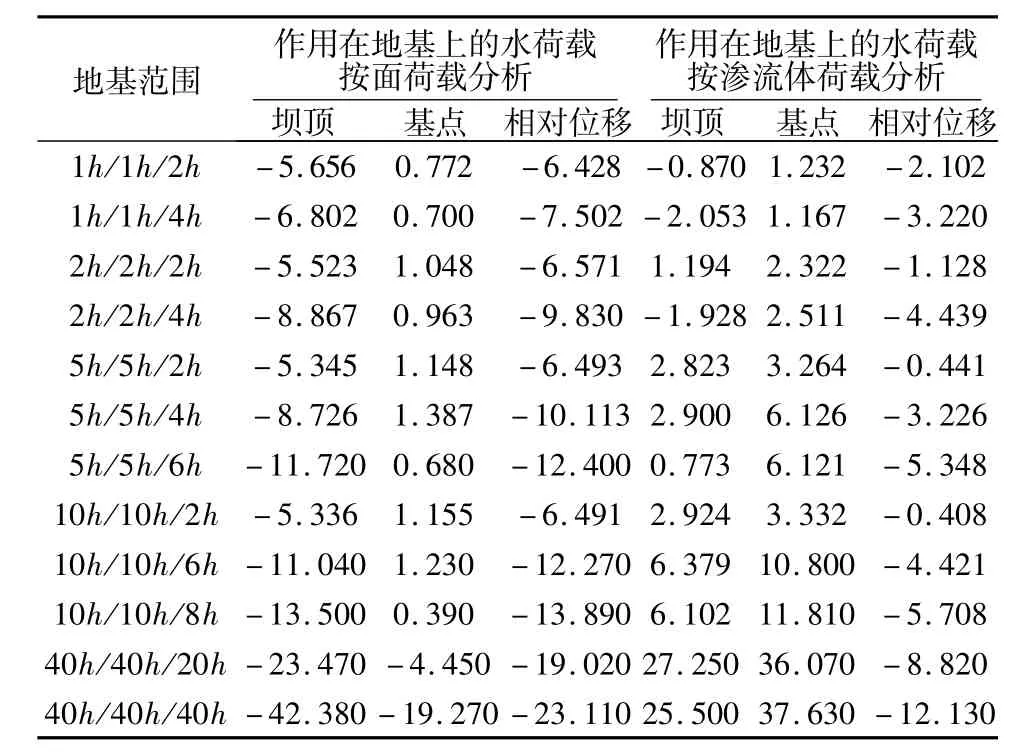
表2 底部完全位移约束时地基变形模量18 GPa时不同工况下坝体水平位移u3Table 2 Dam's horizontal displacement u3 in different load cases with foundation's deformation modulus 18GPa and with rigid constraint at the bottom mm
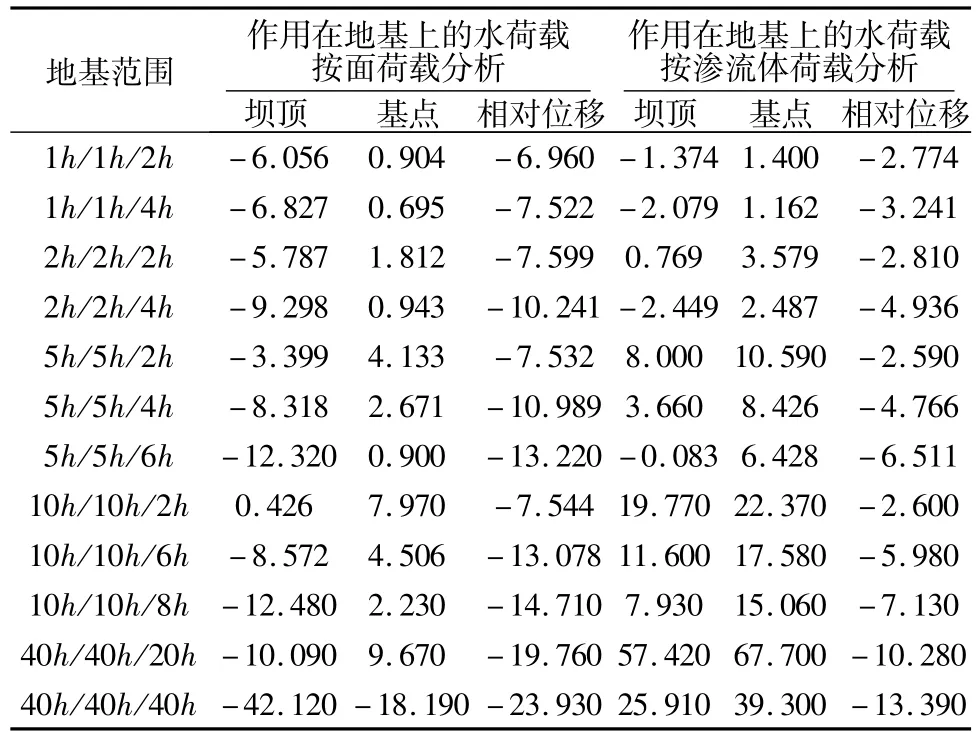
表3 底部刚性支承下地基变形模量18 GPa时不同工况下坝体水平位移u3Table 3 Dam's horizontal displacement u3 under different load cases with foundation's deformation modulus 18GPa and with rigid constraint at the bottom mm
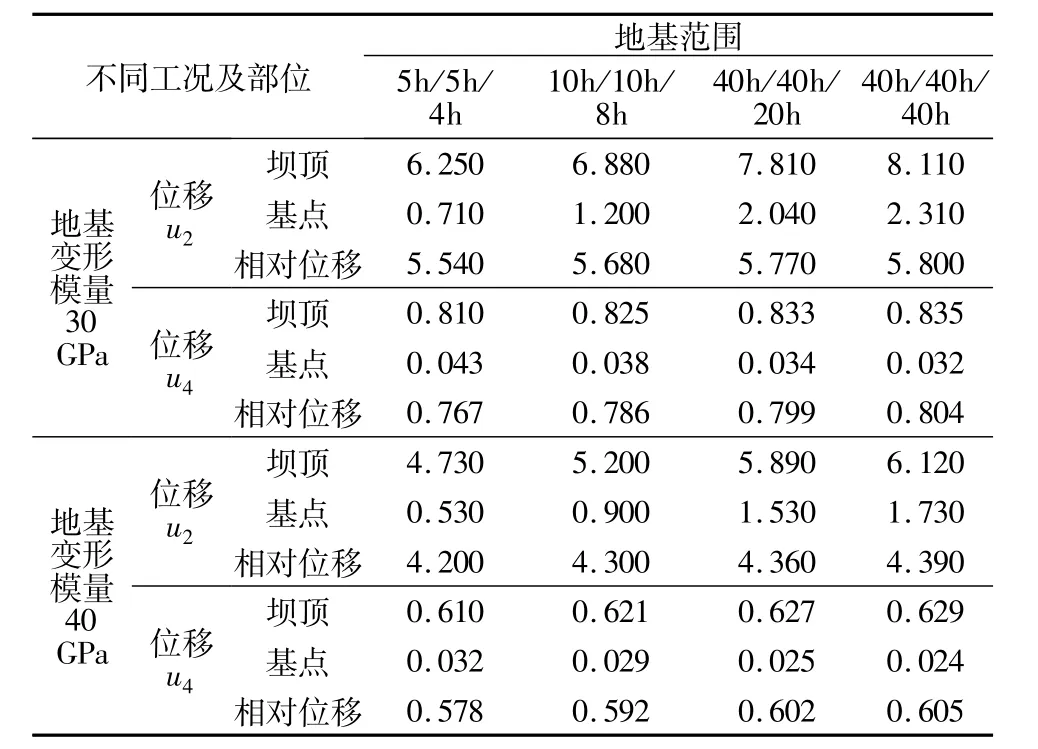
表4 底部完全位移约束下不同工况下坝体水平位移Table 4 Dam's horizontal displacement in different load cases of foundation with rigid constraint at the bottom mm

表5 底部完全位移约束下不同工况下坝体水平位移u3Table 5 Dam's horizontal displacement u3 in different load cases of foundation with rigid constraint at the bottom mm
(3)由表2和表3中的数据还可见,虽然地基底部施加完全位移约束或施加刚性支承约束时,对坝体位移影响较小,但当地基底部施加刚性支承约束时,将在地基底部产生很大的水平向位移。例如地基变形模量18 GPa,底部刚性支承约束,当地基截取范围10h/10h/8h,水荷载作为面荷载和作为渗流体荷载在地基底部产生的水平位移u3分别达到9.784 mm、16.880 mm,这与实际情况不符合,所以建议地基底部施加完全位移约束。
(4)为了获得大坝的“绝对”位移,文献[12]规定“倒垂线钻孔深入基岩深度应参照坝工设计计算结果,达到变形可忽略处。缺少该项计算结果时,可取坝高的1/4~1/2”。由表2、表3和表5的数据可见,当地基截取范围逐渐增大时,无论作用在地基上的水荷载按面荷载考虑还是按渗流体荷载考虑,都将引起基点(坝踵正下方1倍坝高处的岩基)的水平位移逐渐增大。例如表2中,地基范围为10h/10h/8h,水荷载分别作为面荷载和渗流体荷载计算的基点的水平位移 u3为0.390 mm、11.810 mm;当地基范围为40h/40h/40h时,基点的水平位移分别达到-19.270 mm、37.630 mm。由表2、表3和表5的数据还可见,水荷载作为渗流体荷载引起的基点水平位移大于水荷载作为面荷载引起的基点的水平位移。目前,由于工程上常将倒垂线锚固在岩基深处,并认为该倒垂线测值可作为“绝对”位移,当考虑作用在地基上的水荷载时,由上述分析可见,倒垂线测值作为绝对位移的认识是有局限性的。为了获得精度良好的参数反演值,必须考虑到基点的位移,应采用大坝有限元数值计算的坝顶位移和基点位移的相对值,联合实测位移分离出的水压分量进行参数反分析。
(5)随着地基变形模量增加,在建基面上产生的内力使地基变形而引起的位移u2、作用在地基上的水荷载引起坝体的位移u3以及坝基面扬压力引起坝体的位移u4在总位移分量的比例逐渐减小。例如地基范围10h/10h/8h,底部完全位移约束,作用在地基上的水荷载按渗流体积力分析,地基变形模量18 GPa时u1=12.380 mm、u2=9.310 mm、u3=-5.708 mm、u4=1.299 mm;地基变形模量 30 GPa时 u1=12.380 mm、u2=5.680 mm、u3=-3.289 mm、u4=0.786 mm;地基变形模量40 GPa时 u1=12.380 mm、u2=4.300 mm、u3=-2.383 mm、u4=0.592 mm。由表中数据还可见,水平位移u3随着地基截取范围的增大而增大,甚至比水平位移u2还大。
3 结 语
(1)作用在地基上的水荷载作为面荷载和作为渗流体荷载,引起坝体的位移差别很大。虽然地基底部施加完全位移约束或施加刚性支承约束,对水荷载作用下的坝体位移影响较小,但由于当地基底部施加刚性支承约束时,将在地基底部产生很大的水平向位移,建议地基底部施加完全位移约束。
(2)当地基截取范围逐渐增大时,无论作用在地基上的水荷载按面荷载考虑还是按渗流体荷载考虑,都将引起参考基点的水平位移逐渐增大。而且水荷载作为渗流体荷载引起的参考基点的水平位移大于水荷载作为面荷载引起的参考基点的水平位移。由于工程上常将倒垂线锚固在岩基深处,并认为该倒垂线测值可作为“绝对”位移,当考虑作用在地基上的水荷载时,由分析可见,倒垂线测值作为绝对位移的认识是有局限性的。为了获得精度良好的参数反演值,必须考虑到参考基点的位移,应采用大坝有限元数值计算的坝顶位移和基点位移的相对值,联合实测位移分离出的水压分量进行参数反分析。这在大坝工程上进行反分析时值得注意。
(3)实际地基是透水性材料,当采用运行期的原型位移监测值联合大坝有限元数值计算进行反分析时,作用在地基上的水荷载一般应按渗流体荷载分析。由于水在裂隙或孔隙中渗流存在时间效应,这导致水荷载是作为面荷载还是作为渗流体荷载分析不确定,因而属于计算荷载不确定问题,该问题应基于原型监测值反分析确定。
(4)实际地基为有限深地基,该有限压缩层厚度可由外荷载(例如渗流体荷载等)作用下的地基附加应力与自重应力的比值为0.1来确定(对于三维问题,左右岸宽度可由地基附加水平向应力与μ(1-μ)倍地基自重应力的比值为0.1来确定(μ为岩基泊松比),或由实测值反分析确定,然后向上下游截取与地基深度相同的范围,以建立相应的大坝有限元模型。
[1] 吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.
[2] 李珍照.大坝安全监测[M].北京:中国电力出版社,1997.
[3] SL 282—2003,混凝土拱坝设计规范[S].
[4] 林继镛.水工建筑物[M].北京:中国水利水电出版社,2007.
[5] 赵代深.重力坝水荷载的计算[J].水利学报,1984,15(7):53-55.
[6] 潘家铮.坝体有限元分析中的水荷载问题[J].水力发电,1984,10(3):21-26.
[7] 王 媛,速宝玉.坝基应力计算中的水荷载组合形式[J].勘察科学技术 ,1995,(3):3-7.
[8] 黄耀英,沈振中,吴中如.Marc软件在分析渗流场和渗流力中的应用[J].河海大学学报(自然科学版),2006,34(5):509-512.
[9] 张有天.岩石水力学与工程[M].北京:中国水利水电出版社,2005.
[10]王 媛.裂隙岩体渗流及其应力的全耦合分析[D].南京:河海大学,1995.
[11]吴中如,顾冲时.大坝原型反分析及其应用[M].南京:江苏科学技术出版社,2000.
[12]DL/T 5178—2003,混凝土坝安全监测技术规范[S].
